Орбитальный угловой момент и топологический заряд структурно-устойчивых лазерных пучков

Структурно-устойчивые лазерные пучки (СУЛП) интересны тем, что при своем распространении в свободном пространстве они сохраняют структуру распределения интенсивности в своем сечении, изменяются только в масштабе и могут вращаться вокруг оптической оси [1–3]. Вихревые лазерные пучки являются частным случаем СУЛП [4]. Интерес к исследованию СУЛП вызван тем, что они широко используются на практике в задачах беспроводной телекоммуникации [5], манипулирования микрообъектами [6], оптической микроскопии [7] и квантовой информатике [8]. В оптике известны различные варианты описания СУЛП. Например, описываются они, как спиральные лазерные пучки, с помощью аналитической функции с вихревым аргументом x +i y [9], с помощью произведения нулей интенсивности [10], в виде суперпозиции мод Лагерра–Гаусса [11] или Эрмита–Гаусса [12]. Среди структурно-стабильных пучков есть пучки, интенсивность в сечении которых вращается, когда пучки распространяются в свободном пространстве [13, 14]. А есть структурно-стабильные пучки, которые распространяются без вращения, изменяясь только в масштабе [15]. СУЛП могут нести орбитальный угловой момент (ОУМ) [16, 17] и топологический заряд (ТЗ) [18, 19]. Однако не для всех типов СУЛП найдены аналитические формулы для расчета ОУМ и

ТЗ при любых комплексных коэффициентах в суперпозициях. Например, ОУМ для СУЛП в виде суперпозиции мод Эрмита–Гаусса найден в [20], а для суперпозиции мод Лагерра–Гаусса найден в [21]. Но для этих суперпозиций нельзя найти топологический заряд при любых весовых коэффициентах. И наоборот, если представить СУЛП в виде произведения множителей, задающих местоположение нулей интенсивности, то топологический заряд такого пучка будет равен числу его нулей интенсивности, с учетом их вырожденности [22]. Но ОУМ такого пучка аналитически найти затруднительно.

В данной работе мы рассматриваем новый тип СУЛП, комплексная амплитуда которых является многочленом конечной степени с произвольными комплексными коэффициентами и с гауссовой огибающей. ТЗ такого семейства пучков равен степени многочлена, а для ОУМ получено выражение, справедливое для произвольных коэффициентов. Рассмотрен также пример СУЛП, который назван вращающимся пучком Лагерра–Гаусса (ЛГ). Его ТЗ равен радиальному индексу многочлена Лагерра, зависящему от радиальной переменной, а все нули интенсивности расположены на прямой линии, исходящей из оптической оси, и находятся только с одной стороны от оптической оси. Эти нули вращаются вместе с распределением интенсивности, когда пучок распространяется в свободном пространстве.

1. Разные типы структурно-устойчивых лазерных пучков

В [23] показано, что комплексная функция вида

\      1         (       r 2       , re i^ ^

E ( ^r , ф , z ) = , ,exp —      I f \— aI ^,     (1)

q ( z )     L w² q ( z ) J L wq ( z ) J

где ( r , φ, z ) – цилиндрические координаты, w – радиус перетяжки гауссова пучка, q ( z ) = 1 + iz / z 0 , z ₀ = к w2/ X -расстояние Рэлея, λ – длина волны, f ( x ± iy ) – произвольная целая аналитическая функция, которая является решением параксиального уравнения Гельмгольца:

Э E Э² E Э² E _n 2 ik — +---+---= 0.

Э z   Э x ²    Э y ²

В (2) ( x , y , z ) – декартовы координаты, k – волновое число монохроматического света. В общем случае функция f ( x ) может иметь счетное число нулей (корней) и тогда ТЗ пучка (1) будет бесконечный. Такие пучки с бесконечным ТЗ рассматривались, например, в [24]. Поэтому ограничимся далее рассмотрением структурно-инвариантных пучков (1) с конечным числом нулей интенсивности:

, X 1 I      r ² I

E (r, ф,z) = ,/'xP —T7T Ix q(z)    I w2 q (z) J n_ f-^ ф         i?i фm хПrme— I, m=i L wq (z)    w j

где ( r m , φ m ) – полярные координаты нулей интенсивности в начальной плоскости. Cветовое поле (3) имеет n простых (невырожденных) комплексных нулей, и поэтому его ТЗ равен n . Действительно, если подставить выражение (3) в формулу М. Берри для расчета ТЗ [25]:

1 г T I 2f     1 Э E ( r , ф , z ) , 1

TC = — lim Im <--- ——— d ф k ,    (4)

2 л r ⁴”     [ 0 E ( r , ф , z )      Эф J

где Im – мнимая часть числа, lim – предел при стремлении радиальной переменной r к бесконечности, то получим, что TC= n [26].

Световые поля (1) и (3) структурно устойчивы, так как при распространении в свободном пространстве вдоль оптической оси z распределение интенсивности в поперечном сечении сохраняет свой вид, изменяясь только масштабно (пучок расходится) и вращаясь вокруг оптической оси. Действительно, из (3) видно, что нули интенсивности при распространении пучка будут удаляться от оптической оси и поворачиваться против часовой стрелки согласно уравнениям:

z ²

r m ( z ) = m 1 + —, i                V z o ²

ф _m ( z ) = ф _m + arCtg

Из (5) видно, что нули интенсивности удаляются от оптической оси с ростом z так же, как и увеличивается радиус гауссова пучка:

z ²

w ( z ) = w q ( z ) = w (1 + — . z 0 ²

Другой тип структурно-устойчивых лазерных пучков описывается комплексной амплитудой в виде суперпозиции мод Эрмита–Гаусса (ЭГ) со специально подобранными индексами [26]:

E ⁽ x , y ^,0) = -1—exp q ( z )

r2 I ■ , , -----------I e - in ¥( z) x w2 q (z) J

'     2 y

_L ^wq ^{( z} ) _?

где ψ( z ) =arctg( z / z 0 ) – фаза Гоу, C k – произвольные комплексные коэффициенты, H m ( x ) – многочлены Эрмита. Орбитальный угловой момент семейства пучков (7) можно найти по общей формуле, полученной в [27]:

2 § ( m + 1)!( n - m )!Im ( C m * C_m + 1 )

J z _ m = 0 _______________________________

Wⁿ               2

A m!(n - m)! |Cm| m =0

где J z – продольная проекция вектора ОУМ скалярного поля (7), W – мощность (энергия) пучка (7). Топологический заряд для любых коэффициентов (7) найти не удается. Однако это можно сделать при специально подобранных коэффициентах. Например, когда коэффициенты в (7) являются биномиальными коэффициентами с дополнительным множителем степенного вида

C

m

i^mn !

m !( n - m )!

то ТЗ пучков (7) будет равен TC= n [26]. Заметим, что СУЛП (7), в отличие от СУЛП (1), (3), при распространении в свободном пространстве не вращаются, так как у всех пучков в суперпозиции одинаковая фаза Гоу, равная n ψ( z ).

Еще один тип СУЛП описывается комплексной амплитудой в виде осевой суперпозиции мод Лагерра– Гаусса (ЛГ):

^{E ( r ,} Ф ^{, z} ) =       ^x

q ( z )

I r2                z J x exp\--— - i (n + 1)ф(z) I x w2q(z)

[ n 2 ]

x A Cm m=0

reiф w q(z)

n-2 m        /

J^{n - 2 m} L_m

2 r ²

w ² q ( z ) ²

.

Суперпозиция (10) является модой (структурноустойчивая), то есть при распространении в свободном

пространстве распределение интенсивности сохраняет свой вид, изменяясь только масштабно и не вращаясь, так как фаза Гоу у всех пучков одинаковая. Орбитальный угловой момент суперпозиции (10) можно найти по формуле, аналогичной (8):

^[ ^ 21                                      .-..      2

E 4 m ( n - 2 m )( n - m )! ( m ! ) | C m|

Jz_ _ m =0 __________________________________

W~      ^[ П 2¹                    .-1.    ,2

^4m(n-m)!(m!) |Cm| m =0

Из (1) следует, что (14) получилось, когда в качестве аналитической функции f ( x ) был выбран комплексный многочлен степени n . Пучок (14) при распространении в свободном пространстве будет вращаться вокруг оптической оси против часовой стрелки. Действительно, интенсивность пучка (14) будет иметь вид:

.

Топологический заряд светового поля (10) при произвольных коэффициентах найти нельзя, так как задача сводится к нахождению ТЗ суперпозиции оптических вихрей [26]:

n

E ( r >>  1, ф , z = 0) = e -( ^r / w ^{)2 + in} v I — | x I w )

[n21    (-2)m x E C “—7“exp (-2imф). m=0     m!      4

Из (12) видно, что при больших r выражение для комплексной амплитуды (10) представляет собой комплексный многочлен от r exp(-2iφ) степени n при r = 1 . По основной теореме алгебры такой комплексный многочлен имеет столько корней с учетом их вырожденности, сколько их лежит в круге радиуса r = 1. Это число корней аналитически при произвольных коэффициентах C m получить нельзя. Можно найти ТЗ пучка (10) при некоторых специальных коэффициентах. Например, если n – четное число и коэффициенты в (12) равны

C

m

( n/ 2 ) !

(-2)m (n/2-m)!

то ТЗ светового поля (10) будет равен TC = n /2.

2. Структурно-устойчивые лазерные пучки в виде суперпозиции однокольцевых пучков Лагерра–Гаусса

В предыдущем параграфе мы рассмотрели разные типы структурно-устойчивых пучков (3), (7), (10) и показали, что у них нельзя одновременно найти аналитически ТЗ и ОУМ при произвольных комплексных коэффициентах. В этом параграфе мы рассмотрим еще одно семейство СУЛП, у которых можно одновременно аналитически определить и ТЗ, и ОУМ при произвольных комплексных коэффициентах. Если в (10) заменить все многочлены Лагерра на 1, то комплексная амплитуда будет иметь вид:

E ( r , ф , z ) = q ( z ) ¹ exp

— ²       I

—---I x w2 q (z) j

I ^{( r} , ф ^z ) = I E ^{( r} , ф , ^z )l = q ^{( z} ) exp ■

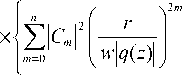
n

+ 2E CmCp| m < p

n x E C m=0

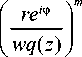
2 r ²

w ² q ( z ) ²

X

/        \ ^{m +} P

r

^ wq (z )l;

x (15)

x cos [ ( m - p ) ( ф-ф ( z ) ) + arg C m - arg C p ] > .

Из (15) видно, что распределение интенсивности будет сохранять свою структуру, если разность

ф - arctg( z / z ₀) = const

не будет зависеть от z . Уравнение (16) означает, что при смещении пучка (14) вдоль оптической оси азимутальный угол должен увеличиться на величину фазы Гоу, чтобы распределение интенсивности сохранило свой вид. Из (14) также видно, что в повернутых и от-масштабированных координатах

(        2       '

r ⁽ z ) = rw ^{- 1} I 1 ⁺ ^ I

I z o2 j

<

ф ( z ) = ф - arctg

пучок (14) будет сохранять свой исходный вид.

Топологический заряд пучка (14) равен n . Это следует из основной теоремы алгебры [28, 29], которая утверждает, что любой комплексный многочлен степени n имеет ровно n комплексных корней с учетом их вырожденности. Поэтому ТЗ структурно-устойчивого пучка (14) будет равен TC= n . ОУМ пучка (14) также можно найти из соотношения, аналогичного (8) и (11):

J z W

±m 2 ^- -m m !| C m |2

m = 0

n

E 2-m (m!) Cm I m=0

3. Примеры структурно-устойчивых пучков, амплитуда которых описывается ортогональными многочленами

В качестве многочлена в (14) можно взять любой из известных ортогональных многочленов (Якоби, Лежандра, Чебышева, Эрмита, Лагерра и т.д.) [30]. Рассмотрим для примера случай, когда многочлен в (14) является многочленом Лагерра.

Тогда коэффициенты в (14) примут вид:

С ^    ( - 1) m ( n + p )!

m !( n - m )!( p + m )!

где n и p – индексы многочлена Лагерра L_n^p ( x ). Тогда вместо (14) можно записать комплексную амплитуду структурно-устойчивого вращающегося лазерного пучка Лагерра–Гаусса вида:

E n , p , + ⁽ r , ф , z ) = —1- X q ( z )

X exp

ILI w2 q (z)J ^ wq (z)

Интересно, что у вращающегося пучка ЛГ (20) топологический заряд равен радиальному индексу многочлена Лагерра TC= n , а не азимутальному индексу, как у обычных пучков ЛГ:

E n , m , + ( Г , ф Z ) =

1-------T X q ( z )

В центре пучка (20) на оптической оси интенсивность всегда будет отлична от нуля, так как

L p (0) - ^ p^ n ! p !

.

Все указанные выше особенности вращающегося пучка ЛГ будут подтверждены в параграфе моделирования.

4. Результаты моделирования

Моделирование СУЛП проводилось по формулам (14) и (20). Параметры расчёта: длина волны λ =532 нм, радиус перетяжки w 0 = 1 мм, радиальный и азимутальный индексы многочлена Лагерра в (20): n = 5, p =2. На рис. 1 показаны интенсивность (рис. 1 а , в , д ) и фаза (рис. 1 б , г , е ) вращающегося пучка ЛГ (20) в начальной плоскости (рис. 1 а , б ), на расстоянии Рэлея z = z 0 (рис. 1 в , г ) и в дальней зоне на расстоянии z =5 z 0 (рис. 1 д , е ). Размеры кадров: | x |, | y | ≤ 2,5 мм (рис. 1 а , в ), | x |, | y | ≤ 10 мм (рис. 1 д ) и | x |, | y | ≤ 40 мм (рис. 1 б , г , е ).

I r2                                          I

X exp--- i (2 n + m + 1) ^ ( z ) X

I w ² q ( z )                     J

Из (20) следует, что с помощью изменения азимутального индекса p можно управлять ОУМ пучка, увеличивая или уменьшая расстояние между нулями интенсивности. При этом ТЗ пучка не будет изменяться. Орбитальный угловой момент вращающегося пучка ЛГ (20) находится с помощью (18), где коэффициенты берутся из уравнения (19). Многочлен Лагерра в (20) имеет n простых действительных корней. Чтобы определить, где они находятся, приравняем нулю мнимую часть аргумента многочлена Лагерра в (20), получим:

sin ф- arctg z = 0, Г    4 z 0 JJ

I z I ф = arctg     + та, s = 0,1.

I z 0 J

Из (22) видно, что при z =0 корни многочлена Ла-герра или нули интенсивности пучка (20) находятся на горизонтальной оси, а при больших z в дальнем поле нули интенсивности повернутся и будут располагаться на вертикальной оси. Причем все нули интенсивности будут лежать не на всей оси (горизонтальной при z =0 или вертикальной при большом z ), а только на положительной ее части, так как многочлен Лагерра при отрицательных значениях аргумента не имеет корней:

lp (-r) -1  ,,(p+n)!r; ,, > 0.

_{m - 0} m !( n - m )!( p + m )!

Рис. 1. Распределение интенсивности (а, в, д) и фазы (б, г, е) для вращающегося пучка ЛГ (20) при n = 5. Кружками отмечены оптические вихри

На рис. 1а, в, д видно, что интенсивность имеет вид асимметричного эллиптического гауссова пятна, смещенного с оптической оси, который при распространении вращается вокруг оптической оси. На расстоянии Рэлея интенсивность повернулась на 45 градусов, а в дальней зоне повернулась почти на 90 градусов. На рис. 1б видно, в начальной плоскости нули интенсивности (центры пяти винтовых дислокаций) лежат на горизонтальной оси справа от центра (оптической оси). Также видно на рис. 1б, что имеются пять линий скачков фазы на 2π. Это означает, что ТЗ пучка на рис. 1 равен 5. На рис. 1г центры оптических вихрей лежат на линии, которая проходит под углом 45 градусов к горизонтальной оси (выделены кружками). А на рис. 1е эти центры оптических вихрей лежат уже на почти вертикальной оси (тоже выделены кружками).

На рис. 2 показаны распределения интенсивности и фазы СУЛП в виде полинома (14) или в виде суперпозиции однокольцевых пучков ЛГ (степень многочлена равна n =5). Размеры кадров: | x |, | y | ≤ 2,5 мм (рис. 2 а , в ) и | x |, | y | ≤ 5 мм (рис. 2 б , г ). На рис. 2 а , б в показаны интенсивность и фаза в начальной плоскости для пучка (14) с коэффициентами: C n 1 = [1,0; 0,9; 0,8; 0,7; 0,6; 0,5], а на рис. 2 в , г показаны интенсивность и фаза в начальной плоскости для пучка (1) но с другими коэффициентами: C n 2 =[1,0; 0,9 e^{i π/6}; 0,8 e^{i 2π/6}; 0,7 e^{i 3π/6}; 0,6 e^{i 4π/6}; 0,5 e^{i 5π/6}]. Видно, что коэффициенты C n 2 отличаются от коэффициентов C n 1 только фазами, а амплитуды у них одинаковые. Поэтому интенсивности на рис. 2 а и рис. 2 в почти одинаковые и отличаются только поворотом на некоторый угол вокруг оптической оси. По фазовой картине на рис. 2 б , г видно, что у обоих пучков имеются 5 оптических вихрей (5 кривых линий скачков фазы на 2π) и ТЗ пучков равен 5.

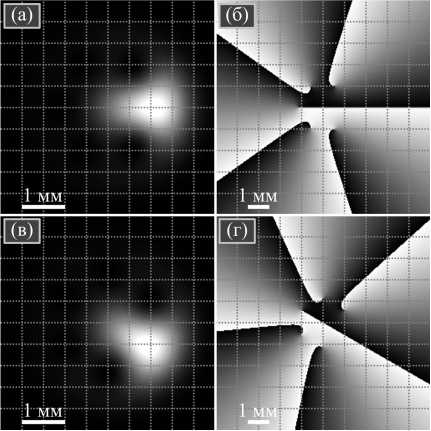
Рис. 2. Распределение интенсивности (а, в) и фазы (б, г) для СУЛП (14) с многочленом степени n = 5 и разными коэффициентами C n1 и C n2

Для распределений с рис. 2 был рассчитан нормированный ОУМ двумя способами: численно по общей формуле для ОУМ [9] и по аналитической формуле (18). Теоретические и численные значения ОУМ совпали и для рис. 2 а , б равны 2,5196 (теория) и 2,5143 (расчёт как в начальной плоскости, так и на расстоянии Рэлея). Для рис. 2 в , г были получены значения 2,5196 (теория), 2,5149 (расчёт в начальной плоскости), 2,5145 (расчёт на расстоянии Рэлея).

На рис. 3 показаны интенсивность (рис. 3 а , в ) и фаза (рис. 3 б , г ) в начальной плоскости пучка (14) также состоящего из суперпозиции 5 однокольцевых пучков ЛГ, но с другими коэффициентами: C n 3 = [1,0; 1,2; 1,4; 1,6; 1,8; 2,0] (рис. 3 а , б ) и C n 4 = [1,0; –1,2; 1,4; –1,6; 1,8; –2,0] (рис. 3 в , г ). Коэффициенты C n 3 и C n 4 отличаются только фазами, у последних коэффициентов фазы чередуются 0 и π. Поэтому интенсивности на рис. 3 а , в зеркально повернуты относительно вертикальной оси. Топологический заряд у пучков (14) не зависит от величины коэффициентов и равен n =5. На рис. 3 б , г видны 5 линий скачков фазы на 2π.

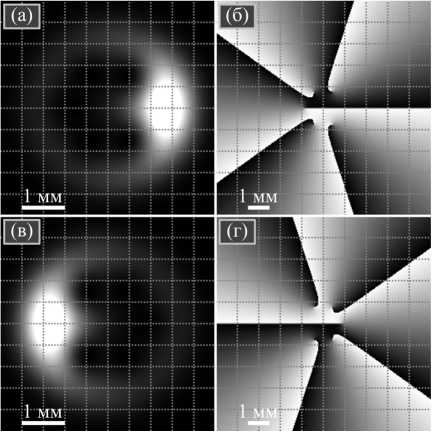
Рис. 3. Распределение интенсивности (а, в) и фазы (б, г) для СУЛП (14) с многочленом степени n = 5 и разными коэффициентами C n3 и C n4

Для распределений на рис. 3 также был рассчитан нормированный ОУМ двумя способами. Теоретические (18) и численные значения ОУМ для обоих полей одинаковы и равны 4,2026 (теория) и 4,1934 (расчёт, как в начальной плоскости, так и на расстоянии Рэлея). Расчетное значение нормированного ОУМ всегда немного меньше точного теоретического потому, что оно рассчитывается с помощью интегрирования не по всему сечению пучка, а только по его центральной части, которая имеет размер кадра (рис. 3).

На рис. 4 показаны интенсивности и фазы СУЛП (14) при n =5 и разных наборов коэффициентов. Кадры интенсивности имеют размер, как и ранее, |x|, |y| ≤ 2,5 мм, а кадры фазы имеют также размер, как и ранее, |x|, |y| ≤ 5 мм. Для пучка на рис. 4а, б коэффициенты равны Cn5=[0,1772;0,5715;0,4997;0,1300;0,9195;0,6661]. Видно, что интенсивность пучка на рис. 4а похожа на интенсивность пучка на рис. 3а. Коэффициенты для пучка на рис. 4в, г имеют вид: Cn6 = [0,4460; – 0,1817; 0,8461; –0,0655; 0,2935; –0,7292]. На распределении интенсивности пучка на рис. 4в уже видны области изолированных нулей интенсивности, но их пока 3, а не 5. А на рис. 4д, е показан СУЛП (14), у которого видны все 5 нулей интенсивностей, так как коэффициенты подобраны специальным образом: Cn7=[0,7159; 0,1559; 0,0066; 0,3692; 0,2428; 0,6799]. На рис. 4ж, з показаны интенсивность и фаза еще одного пучка (14) с коэффициентами Cn8=[0,7316; 0,1817; 0,8542; 0,4196; 0,7175; 0,3024]. Из рис. 4ж видно, что почти вся интенсивность сосредоточена в правой части сечения пучка, а кольцевой и круговой структуры интенсивности пучка уже нет. У всех пучков на рис. 2, 3 и 4 ТЗ равен n = 5.

Рис. 4. Распределение интенсивности (а, в, д, ж) и фазы (б, г, е, з) для СУЛП (14) с многочленом степени n = 5 и случайными коэффициентами C n5 , C n6 , C n7 и C n8 : C n5 = [0,1772; 0,5715; 0,4997; 0,1300; 0,9195; 0,6661] (а, б), C n6 = [0,4460; –0,1817; 0,8461; –0,0655; 0,2935; –0,7292] (в, г), C n7 = [0,7159; 0,1559; 0,0066; 0,3692; 0,2428; 0,6799] (д, е), C n8 = [0,7316; 0,1817; 0,8542; 0,4196; 0,7175; 0,3024] (ж, з)

Рассчитанные значения ОУМ для распределений на рис. 4 равны 4,2408 (рис. 4 а , б , теория) и 4,2316 (рис. 4 а , б , расчёт), 4,1592 (рис. 4 в , г , теория) и 4,1499 (рис. 4 в , г , расчёт), 3,8141 (рис. 4 д , е , теория) и 3,8054

(рис. 4 д , е , расчёт), 2,7479 (рис. 4 ж , з , теория) и 2,7424 (рис. 4 ж , з , расчёт). Численные значения ОУМ в начальной плоскости и на расстоянии Рэлея совпали.

Заключение

В данной работе получены следующие результаты. Рассмотрены разные типы структурно-устойчивых лазерных    пучков,    которые описываются аналитической функцией с вихревым аргументом x+iy (1), в виде произведения изолированных нулей интенсивности (3), суперпозиции пучков Эрмита– Гаусса (7) и суперпозиции пучков Лагерра–Гаусса (10). Для двух последних типов СУЛП получены выражения для расчета ОУМ при любых комплексных коэффициентах (8) и (11). Рассмотрен СУЛП с множителем в виде комплексного многочлена степени n (14), для которого показано, что он имеет ТЗ, равный n, при любых коэффициентах. Также получено выражение для расчета ОУМ такого пучка (18). В качестве примера полиномиальных СУЛП рассмотрен вращающийся пучок ЛГ с вихревым аргументом (20). У такого пучка все нули интенсивности расположены на луче, лежащем в поперечной плоскости, который исходит от оптической оси и вращается против часовой стрелки вместе с распределением интенсивности, когда пучок распространяется в свободном пространстве. В центре (на оптической оси) у вращающихся вихревых пучков ЛГ интенсивность всегда отлична от нуля.

Работа выполнена при поддержке Российского научного фонда (грант №  23-12-00236) в теоретической части и в рамках выполнения работ по Государственному заданию НИЦ «Курчатовский институт» в части моделирования.