Орбитальный угловой момент произвольного осесимметричного светового поля, прошедшего смещённую с оси спиральную фазовую пластинку

В [1, 2] А. Цайлингер предложил регистрировать фотоны, которые рождаются парами в ходе спонтанного параметрического рассеяния в перепутанном состоянии по орбитальному угловому моменту (ОУМ), с помощью смещения центров Гауссова пучка и голограммы «с вилочкой». Он предположил, что при малом смещении между центрами пучка и голограммы формируется линейная комбинация Гауссова пучка и пучка Лагерра – Гаусса. В [3] также экспериментально показано, что можно регистрировать перепутанные по ОУМ стоксовый и антистоксовый фотоны с помощью четырёхволнового смешения в ансамбле «горячих» атомов и при смещении центров Гауссова пучка и голограммы «с вилочкой». Известны также исследования трансформации оптических вихрей и в классическом свете. Под оптическим вихрем здесь понимается лазерный пучок с изолированным нулём интенсивности на оптической оси и спиральной фазой с целым топологическим зарядом. В [4] теоретически изучается влияние на оптический вихрь смещения вдоль оптической оси центра перетяжки Гауссова пучка от плоскости спиральной фазовой пластинки, совмещённой с дифракционной линзой (спиральная линза). В [5] экспериментально исследуется прохождение оптического вихря через набор малых отверстий в непрозрачном экране, центры которых лежат на окружности. Показано, что при этом вырожденный оптический вихрь n-го порядка распадается на n невырожденных оптических вихрей (1-го порядка). В [6] исследуется трансформация оптического вихря с помощью внесения в него разной степени эллиптичности. Эта работа [6] продолжает более ранние работы по исследованию эллиптических оптических вихрей [7, 8]. В [9] предложено формировать оптический вихрь с помощью набора малых отверстий в непрозрачном экране, центры которых расположены на спирали. Небольшие деформации направляющей спирали приводят к искажению формы оптического вихря.

Наиболее близкими по тематике к данной работе являются ранние статьи авторов [10– 12]. В них теоретически и экспериментально исследуются трансформации оптического вихря, которые получаются в результате комплексного смещения исходной функции комплексной амплитуды в декартовой системе координат. Такое смещение приводит к асимметрии оптического вихря: вместо светового кольца (или «пончика») формируется полумесяц. В [10] комплексное смещение координат применено для пучков Бесселя, а в [11] – для пучков Лагерра – Гаусса. В [12] оптический вихрь n -го порядка преобразуется в n оптических вихрей 1-го порядка с помощью использования эллиптического Гауссова пучка, падающего на спиральную фазовую пластинку. В [13] теоретически исследуется дифракция Гауссова пучка на смещённой с оси голограмме с «вилочкой». В [14, 15] получены формулы для полного относительного ОУМ Гауссова пучка со смещённым центром спирального фазового вихря.

Заметим, что при комплексном смещении координат ОУМ пучков Бесселя [10] и Лагерра – Гаусса [11] растёт. Растёт также ОУМ у эллиптического вихрево- го пучка Эрмита – Гаусса [12]. В отличие от них ОУМ асимметричного Гауссова вихря, описанного в [14, 15], убывает с увеличением расстояния между центрами Гауссова пучка и спиральной фазовой пластинки. В [16, 17] получены формулы для полного ОУМ для эллиптических Гауссовых вихрей.

В этой работе мы получили точное выражение для полного относительного ОУМ для случая произвольного (а не только Гауссова) радиально-симметричного распределения интенсивности, дифрагирующего на спиральной фазовой пластинке (СФП), центр которой смещён с оптической оси.

1. Расчёт полного орбитального углового момента

Рассмотрим начальное вихревое световое поле, комплексная амплитуда которого имеет вид:

En (r, ф) = Eо (r) exp (inф),(1)

где ( r , φ) – полярные координаты в начальной плоскости при z =0, n – целое число, равное топологическому заряду СФП с пропусканием:

Tn (ф) = exp (inф),(2)

а E 0 ( r ) – осесимметричная комплексная амплитуда светового поля, падающего на СФП (2) (в дальнейшем «падающая волна»), равная

Eо (г) = A(г)exp(iф(г)),(3)

м 2 п

W = JI E * ( r , ф ) E ( r , ф ) r d r d ф .                  (6)

Известно, что ОУМ зависит от расстояния от начала координат до точки «центра масс» светового поля. И если это расстояние равно нулю, то рассчитанный ОУМ будет минимальным. В нашем случае как раз «центр масс» пучка (3) совмещён с началом координат ( r , φ), а СФП смещена от начала координат на вектор ( r _о, ф _о). Для расчёта нормированного ОУМ подставим в (5) и (6) комплексную амплитуду вида

^E ( ^Г , ф ) = ^E о ( ^Г ) T n ( ^r , ^г о , ф , ф о ) . ⁽⁷⁾

Получим промежуточное выражение перед тем, как выполнять интегрирование по полярному углу:

М 2- I ( ^r ) ^г Г ^{г - г} о СО8 ( ф^-ф о ) ]

Jz = n ----2-----------7------rddгdф ■ о о г + го -2ггocos(ф-фо)

Интеграл по φ в (8) можно вычислить с помощью двух справочных интегралов [18] (выражения 2.5.16.61, 2.5.16.67, 2.5.16.68):

2[        d t        =   2п о г 2 + го2 - 2 ггоСО t   |го2 - г 2| ’

где A ( г ) и у ( г ) — соответственно модуль амплитуды падающей волны (3) и её аргумент, I ( r ) = A ² ( r ) – интенсивность падающего поля. Пусть далее центр СФП (2) смещён с оптической оси на вектор с полярными координатами ( г 0, ф ₀). Тогда пропускание СФП вместо (2) примет вид:

?      cos t d t

* г ² + г _о ² - 2 гг _о cos t

2п г го (го2 - г 2)

^{2 п г} о г ( г ² - г _о ² )

, ^г <  ^г о ,

, ^г >  ^г о .

После вычисления интеграла по φ для нормированного ОУМ светового поля (7) окончательно получим:

T n ( ^Г , ^r 0 , ф , ф о ) =

г exp ( i ф ) - Г о exp ( i ф о )

V r ² + r o ² - 2^ros (ф-ф о )

Далее мы получим простое выражение для ОУМ параксиального светового пучка, сформировавшегося после прохождения осесимметричного светового поля (3) через смещённую СФП (4). В параксиальном случае ОУМ можно заменить проекцией вектора ОУМ на оптическую ось, которую будем вычислять по формуле:

I м 2 n                d                        |

J = Im <[ [ E * ( r , ф ) — E ( r , ф ) r d r d ф^ , Го о          ^д ф

где Im – мнимая часть комплексного числа, E ^* – комплексно сопряжённая функция. Так как величина (5) является инвариантом для любого параксиального светового поля, то рассчитывать её можно в любой плоскости, перпендикулярной оптической оси, и в том числе в начальной плоскости при z =0. Мощность лазерного пучка будем рассчитывать по формуле:

- 1

J

WW = n J I ( г ) r d г J I ( г ) r d г .

м

r ₀

Из (11) видно, что ОУМ зависит только от длины вектора смещения r 0 и не зависит от полярного угла вектора смещения ф _о и от вида волнового фронта падающей волны у ( г ).

Кроме того, так как числитель в (11) всегда меньше или равен знаменателю, то ОУМ будет убывать до нуля при увеличении величины смещения СФП от «центра масс» падающего пучка r 0. Если смещение равно нулю r 0 = 0, то нормированный ОУМ равен топологическому заряду:

J , = n .

W

Заметим, что подынтегральное выражение в (8) равно плотности ОУМ в каждой точке сечения лазерного пучка (7) в начальной плоскости z =0:

nI ( г ) г Г г - ^cos ( ф-ф _о ) ] z г ² + г _о ² - 2 r ^cos ( ф-ф _о )

В начале координат ( r =0) плотность ОУМ (13) всегда равна нулю, так как «плечо» равно нулю. Из (13) следует, что нормированная плотность ОУМ пучка (7) при отсутствии смещения r 0 =0 также равна топологическому заряду, как и полный ОУМ (12):

j z

.

I

Из (18) видно, что с увеличением расстояния от центра СФП до центра перетяжки Гауссова пучка ОУМ уменьшается экспоненциально от n до нуля. Этот результат был получен ранее в [14].

2) Если смещённую с оптической оси СФП осветить плоской волной, ограниченной круглой диафрагмой, то есть интенсивность падающего пучка можно описать функцией

На бесконечности ( r >>  r ₀) плотность ОУМ тоже равна топологическому заряду (14) при любом конечном r ₀. Получается, что на бесконечности смещение центра СФП от «центра масс» пучка не проявляется. Из (13) также следует, что на окружности с радиусом r = r 0 независимо от величины r 0 значение плотности ОУМ равно

. x ( r I 1 1, r <  R , I(r ) = I _o circ — = I_o\

V 1    0     ( R J 0 10, r > R,

то из (11) следует, что ОУМ такого пучка будет равен выражению:

1к = n

I 2^,

во всех точках, кроме точки ф = ф 0 . В этой точке плотность j_z / I не имеет предела (плотность равна n /2 на окружности r = r 0 , стремится к + ^ с внешней стороны окружности и к - ^ с её внутренней стороны). На прямой линии, проходящей через начало координат ( r =0), и под углом ф = ф 0 плотность (13) имеет вид:

nr

L. = Jr - r

I nr

r + ro

, ф = Фо ,

, ф = фо + П.

Из (16) следует, что при r → r ₀, r <  r ₀ плотность ОУМ (13) стремится к - ^ , а при r ^ r ₀, r >  r ₀ плотность ОУМ (13) стремится к + ~ . В точке с координатами ( r ₀, ф ₀) при любом направлении подхода к этой точке плотность стремится к бесконечности, так как эта точка сингулярности. Интересно, что эта особенность плотности ОУМ (стремление к бесконечности в точке ( r ₀, ф ₀)) проявляется только при r ₀>0, а при r 0 = 0 плотность ОУМ в точке сингулярности равна топологическому заряду (14), так как «плечо» равно нулю. Интересно также отметить, что плотность ОУМ (13) может быть отрицательной. Например, из (16) видно, что на луче ф = ф ₀ при 0< r <  r ₀ плотность ОУМ меньше нуля. То есть поток энергии в этих точках вращается в обратную сторону.

Вернёмся к уравнению (11) для нормированного ОУМ и получим на его основе частные случаи.

1) Если смещённую СФП освещает несмещённый Гауссов пучок с радиусом перетяжки w и распределением интенсивности в перетяжке ( I ₀ – постоянная)

I 2 r2 I

I(r) = 10expl--у I, I w J

то из (11) следует, что ОУМ Гауссова лазерного пучка, прошедшего смещённую СФП, будет равен:

J

— = n exp W

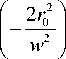
J ' = n 1 — r

W I   R2

.

Из (20) следует, что с ростом r 0 от нуля до R нормированный ОУМ уменьшается от n до нуля квадратично. При любом r 0 >  R из (11) следует, что ОУМ будет равен нулю.

3) Если ограничить плоскую волну, падающую на смещённую СФП, не круглой, а кольцевой диафрагмой с внешним радиусом R ₂ и внутренним радиусом R ₁, то интенсивность освещающего пучка будет равна:

I ( r ) = I0

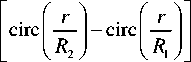
Нормированный ОУМ (11) такого пучка будет равен:

n , r <  R 1 ,

J=.

W

I R 2 n ²

I R ²

r ² I _

"Г2" I , ^R 1 <  ^r 0 <  ^R 2 , ^R 1 J

0, г >  R 2 .

Из (22) следует интересное свойство такого вихревого пучка. Если освещать СФП плоской волной, ограниченной кольцевой диафрагмой, то при любом расположении центра СФП внутри круга с внутренним радиусом R ₁ нормированный ОУМ пучка будет равен топологическому заряду n .

2. Численное моделирование

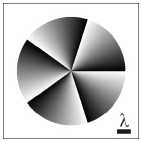
На рис. 1 показаны распределения фазы в начальной плоскости, рассчитанные по формуле (4) (с учётом ограничения круглой диафрагмой (19)), а также распределения интенсивности и фазы на расстоянии z = 15 X , рассчитанные методом распространения пучка ( Beam Propagation Method ) в программе RSoft BeamPROP, для следующих значений параметров: длина волны X = 532 нм, топологический заряд СФП n = 5, радиус диафрагмы R = 4 X , расчётная область -5 X < x , y < 5 X (в начальной плоскости) и -12,5 X <  x , y < 12,5 X (на расстоянии z = 15 X ), смещение СФП r ₀ = 0 (рис. 1 а - в ), r ₀ = 0,5 X (рис. 1 г - е ), r ₀ = X (рис. 1 ж - и ), r ₀ = 2 X (рис. 1 к - м ), r ₀ = 4 X (рис. 1 н - п ).

а)

д)

г)

н)

о)

б)

Рис. 1. Распределения фазы в начальной плоскости и распределения интенсивности и фазы на расстоянии z = 15λдля длины волны λ= 532 нм, топологического заряда СФП n = 5, радиуса диафрагмы R = 4λ, смещения СФП r0 = 0

(а – в), r₀ = 0,5 λ (г – е), r₀ = λ (ж – и), r₀ = 2 λ (к – м), r₀ = 4 λ

(н – п). Расчётная область –5 λ ≤ x, y ≤ 5 λ (в начальной плоскости) и –12,5 λ ≤ x, y ≤ 12,5 λ (на расстоянии z = 15 λ )

В табл. 1 приведены значения нормированного ОУМ для разных смещений СФП, вычисленные по формуле (20).

Табл. 1. Нормированный ОУМ для разных смещений СФП от центра круглой диафрагмы

r 0 / λ	0,00	0,50	1,00	2,00	4,00
J z / I	5,00	4,92	4,69	3,75	0,00

Из табл. 1 и из формулы (20) видно, что смещение центра СФП от центра диафрагмы на 10% от её радиуса меняет ОУМ лишь на 1 %, и кольцевая структура интенсивности сохраняется, несмотря на её асимметричность.

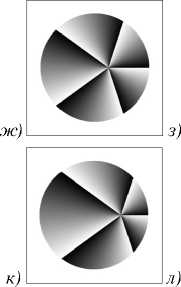
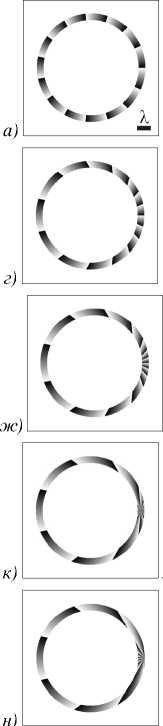
На рис. 2 показаны распределения фазы в начальной плоскости, рассчитанные по формуле (4) (с учётом ограничения кольцевой диафрагмой (21)), а также распределения интенсивности и фазы на расстоянии z = 15λ, рассчитанные методом распространения пучка (Beam Propagation Method) в программе RSoft BeamPROP, для следующих значений параметров: длина волны λ = 532 нм, топологический заряд СФП n = 15, внутренний и внешний радиусы диафрагмы R1 = 3,5λ и R2=4λ, расчётная область –5λ ≤ x, y ≤ 5λ (в начальной плоскости) и –25λ ≤ x, y ≤ 25λ (на расстоянии z = 15λ), смещение СФП r0=0 (рис. 2а – в), r0=2λ (рис. 2г – е), r0=3λ (рис. 2ж – и), r0 = 3,75λ (рис. 2к – м), r0 =4λ (рис. 2н – п).

б)

д)

з)

Рис. 2. Распределения фазы в начальной плоскости и распределения интенсивности и фазы на расстоянии z = 15 λ для длины волны λ = 532 нм, топологического заряда СФП n = 15, внутреннего и внешнего радиусов кольцевой диафрагмы R₁ = 3,5 λ и R₂ = 4 λ , смещения СФП r₀ = 0 (а – в), r₀ = 2 λ (г – е), r₀ = 3 λ (ж – и), r₀ = 3,75 λ (к – м), r₀ = 4 λ (н – п). Расчётная область –5 λ ≤ x, y ≤ 5 λ (в начальной плоскости) и –25 λ ≤ x, y ≤ 25 λ (на расстоянии z = 15 λ )

В табл. 2 приведены значения нормированного ОУМ для разных смещений СФП, вычисленные по формуле (22).

Табл. 2. Нормированный ОУМ для разных смещений СФП от центра кольцевой диафрагмы

r 0 / λ	0,00	2,00	3,00	3,75	4,00
J z / I	15,00	15,00	15,00	7,75	0,00

Из рис. 2а – и и табл. 2 видно, что, несмотря на разный вид интенсивности (кольцо и полукольцо), нормированный ОУМ этих полей одинаков и равен 15. Кроме того, эти поля обладают слабой дифракцией из-за того, что их амплитуда отлична от нуля на узком кольце (как у мод Бесселя в дальней зоне). Видно также, что при увеличении r0 первое светлое кольцо не только искажается и становится полукольцом, но и уменьшается его размер.

Заключение

В данной работе получена простая формула для относительного полного орбитального углового момента параксиального светового пучка с произвольной (не только Гауссовой) радиально-симметричной комплексной амплитудой, прошедшего через спиральную фазовую пластинку, центр которой смещён с оптической оси. Формула показывает, что ОУМ равен нулю, если падающая на СФП плоская волна ограничена диафрагмой, а центр СФП находится за пределами этой диафрагмы. Если падающая на СФП плоская волна ограничена кольцевой диафрагмой, то, в какой бы точке внутри затенённого круга кольцевой диафрагмы ни находился центр СФП, полный ОУМ пучка одинаковый. То есть целесообразно освещать СФП пучками с кольцевым распределением интенсивности, так как при этом неточное совмещение центра СФП и центра кольцевого распределения интенсивности не будет влиять на полный ОУМ пучка. Также получено выражение для плотности ОУМ такого пучка в начальной плоскости. Результаты работы могут найти применение в оптической передаче информации и манипуляции микрообъектами.

Работа выполнена при поддержке Федерального агентства научных организаций (соглашение № 007-ГЗ/Ч3363/26) в параграфе «Численное моделирование» и Российского научного фонда (грант 17-19-01186) в параграфе «Расчёт полного орбитального углового момента».