Орбитальный угловой момент структурно-устойчивых лазерных пучков

В последнее время уделяется большое внимание структурированному свету. Имеется несколько обзорных работ, в которых описываются генерация и детектирование такого света [1, 2]. Такой свет можно генерировать как с помощью лазеров [3, 4], так и с помощью оптических компонент вне резонатора (например, с помощью астигматического конвертора [5]). Структурированный свет – это свет, имеющий пространственную поперечную (например, пучки Эрмита–Гаусса (ЭГ) или Лагерра–Гаусса [6]), продольную (например, пучки Эйри [7]), поляризационную (например, пучки с радиальной или азимутальной поляризацией [8]) и временную (например, пространственно-временные оптические вихри [9, 10]) структуру. Структурно-устойчивые пучки являются частным случаем структурированных пучков и могут быть представлены разными способами. Например, с помощью множества смещенных оптических вихрей одного знака, внедренных в Гауссов пучок [11], или с помощью конечной суммы пучков ЭГ [12], или с помощью ряда [13]. Интересно, что в работе [14] авторы анализируют с помощью конечной суммы пучков ЭГ с комплексными коэффициентами возмущение моды Лагерра–Гаусса. Фактически в [14] исследуется специальный тип возмущений пучка Лагерра–Гаусса, а именно такой, что возмущенные пучки по-прежнему остаются структурноустойчивыми.

В данной работе мы рассмотрим структурноустойчивые лазерные пучки, комплексная амплитуда которых является конечной суммой пучков ЭГ. Мы получим общее выражение для орбитального углового момента (ОУМ) таких пучков и приведем несколько конкретных примеров выбора весовых коэффициентов у суперпозиции пучков ЭГ, при которых получаются разные значения ОУМ. Мы покажем, что максимальный нормированный на мощность пучка ОУМ равен максимальному номеру многочлена Эрмита, входящего в эту сумму.

• 1.    Орбитальный угловой момент

Под структурно-устойчивыми (их еще называют структурированными Гауссовыми) пучками будем понимать параксиальные пучки, комплексная амплитуда которых равна конечной сумме пучков ЭГ с номерами, сумма которых постоянна и равна N :

С x ² + V ² ^

SGn (x, V) = exp I--— IX

• V

x Y r н  ^{С x} )н ^{С V} 1

• X A CpHN-p       Hp,

• p = 0         V w ) V w )

где w – радиус перетяжки Гауссова пучка, C p – комплексные коэффициенты, H p ( x ) – многочлены Эрмита, удовлетворяющие рекуррентным соотношениям:

H n ( x ) = 2 xH n - 1 ( x ) - 2( n - 1) H n - 2 ( x ),               (2)

H 0 ( x ) = 1, H 1 ( x ) = 2 x .

Пучки ЭГ являются структурно-устойчивыми, то есть при распространении сохраняют свой вид, из- меняясь масштабно. Преобразование Френеля сохраняет пучок ЭГ:

XX

' ik Iff ' x 2 + y 2 I HG n , m fe n, z ) = l --— I     exp l — |x

I 2nz J-L-L I    w2 J

„ IV2x L 'V2y I

X Hn --- Hm --- X ww

где E ( x , y ) – комплексно сопряженная амплитуда, Im – мнимая часть числа. Подставляя (1) в (5) и (6) и пользуясь ортогональностью многочленов Эрмита и известными формулами для их производной

x exp 2z- ( x ² + y ² + c ² +n ² - 2 x £- 2 y n ) dxdy =

X

J exp ( - x ² ) H n ( x ) H m ( x ) = Vn 2 n n ! 5 n , m

-X dHn (x)

-------= 2nHn-i (x), dx

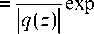
где δ n , m – символ Кронекера, получим общие формулы для ОУМ и мощности пучка (1):

I

^X exp

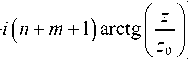
c ² +n ²

w ² q ( z ) ²

' У2 x '

X w\q(z )| ,

' y' X w\q ⁽z )| J

где q ( z ) = 1 + iz / z 0 , z 0 = kw ²/2 – длина Рэлея, k – волновое число света, ( x, y ) и ( ξ, η ) – поперечные декартовы координаты в начальной плоскости и на расстоянии z , z – третья декартова координата, направленная вдоль оптической оси пучка. Из (3) видно, пучки ЭГ, у которых сумма номеров постоянная n + m = N , распространяются с одинаковой фазовой скоростью (у них одинаковая фаза Гоу), и поэтому линейная комбинация таких пучков (1) будет структурно-устойчивой.

Если сложить пучки (3) с весовыми коэффициентами C p , получим комплексную амплитуду поля (1) на расстоянии z :

SG n ( x , y , z ) = exp

x2 + y2 + ik (x2 + y2) w2 |q (z)|       2R(z)

X

X

N

Y Ct p=0 q(z

N - p

V2x v wq(z)

и ² y

p

w\q ⁽ z 1’

где R ( z ) = z [1 + ( z 0 / z )²] – радиус кривизны волнового фронта.

Найдем далее общую формулу для расчета нормированного ОУМ структурно-устойчивых Гауссовых пучков (1). Для этого используем известные формулы для расчета ОУМ параксиальных световых полей J z и для расчета мощности пучка W :

XX      /

J_z = Im j J E ( x , y ) l x

-x -x         X

d E ( x , y ) d y

d E ( x , y ) Y, ^ _ze4

- y-------- dxdy , (5) d x   )

X X

W = J J E ( x , y ) E ( x , y ) dxdy ,                     (6)

-X -X

J z =n 2 ^N N ^ ( p + 1)!( N - p )!Im ( C p C p _{+ 1} ) , p = 0

W = n 2 ^{N - 1} ]T p !( N - p )! ( C p C p ) .

p = 0

Нормированный ОУМ (Im – мнимая часть числа) для поля (1) будет иметь вид:

J z W

2 ]T 1 ( p + 1)!( N - p )!Im ( C p C p + 1 ) p = 0

N

^ p !( N - p )! ( C_PC_P ) p = 0

Из (9) следует, что у структурно-устойчивого Гауссова пучка (1) ОУМ будет отличен от нуля, если коэффициенты С p комплексные. И даже достаточно, чтобы коэффициенты С p не все были комплексные, а через одного. Минимальное достаточное условие, чтобы пучок (1) имел ОУМ, – это отличие фазы хотя бы одного коэффициента в сумме (1) от фаз других коэффициентов.

Получим частные случаи из общей формулы (9). Рассмотрим простой случай, когда в сумме (1) отличными от нуля являются только первых два коэффициента C 0 = 1, C 1 = i γ. Тогда ОУМ (9) для такого структурного Гауссова пучка с амплитудой:

SG_n ( x , y ) = exp

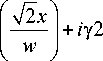
будет равен

Jz =   2y

W 1 + y 2 / N'

x ² + y ² w ²

^H N - 1 w

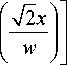
Из (11) видно, при большом N ОУМ пучка (10) определяется величиной γ: J z / W ≈ 2γ. Можно показать, что топологический заряд поля (10) равен N при любых γ >0.

Рассмотрим еще один простой пример, в котором ОУМ будет пропорционален номеру N =2 s + 1. Для этого выберем из суммы (1) отличными от нуля только два слагаемых с соседними номерами:

С ( N - 1)/2 — 1, С ( N + 1)/2 — i ^у ,   ^{N — 2 1 +} 1.              ⁽¹²⁾

Тогда ОУМ (9) такой суммы двух пучков ЭГ

f x ² + V ² J

SG n ( x , у ) — exp I--— IX

I + 1

будет равен

- — ( I + 1)

W

2 у f N + 1 J 2 у 1 + у ² = I 2 J1 + у ² .

Вихревой пучок (13) рассмотрен в [15], а его топологический заряд найден в [16] и равен N .

Приведем пример выбора коэффициентов в (1), при котором ОУМ достигает максимальной величины. Для этого выберем коэффициенты в (1) пропорциональными биноминальным коэффициентам:

С p

N !( i у ) p p !( N - p )!.

Тогда ОУМ (9) пучка (1) с весовыми коэффициентами (15) примет вид:

J — n 2y

W    1 + у ²

.

Структурно-устойчивый Гауссов пучок с коэффициентами (15) можно записать в более простом виде, используя свойство сложения многочленов Эрмита:

SG N ( x , у ) — exp

x ² + у ² J

X w2 I

.f N !( i у ) ^p H   f У2 x J H f V| y

p : 0 p !( N - p )! ^N - p I w I p I w

— exp

-Л ^У -J ( 1 -Y 2 ) N ^/2 H n w ² )

w 1 -у ² _? .

Пучки с амплитудой (17) называются вихревыми пучками Эрмита–Гаусса [17]. При γ = 1 пучок (17) становится модой Лагерра–Гаусса с нулевым радиальным числом ( p =0). При этом все оптические вихри с зарядом 1, находящиеся в действительных нулях многочлена Эрмита, «соединяются» в один оптический вихрь на оптической оси. При этом ОУМ пучка (17) становится максимальным и равным ОУМ пучка Лагерра–Гаусса J z / W = N = l . Топологический заряд пучков (17) найден в [16] и равен N для любого γ.

Если выбрать коэффициенты в (1) в виде:

G_p — C n • m ( a ) — i p cos " ^{- p} a sin m ^{- p} a P n ^{- p} • m ^{- p} ( - cos2 a ),

N — n + m, где Pp,M (x) - многочлены Якоби, то получим пучки Эрмита–Лагерра–Гаусса (ЭЛГ), зависящие от пара-

метра α и рассмотренные в [4]. Заметим, что для пучков ЭЛГ номер N определяет не один пучок, а семейство пучков с разными n и m ( N = m + n ) при заданном параметре α. В [18] найден нормированный ОУМ пучков с коэффициентами (18):

— — ( n - m ) sin 2 a . W

Номера n и m в (18) и (19) можно связать с азимутальным l и радиальным p номерами пучка ЛГ: N = n + m =2 p + l , n = p + l , m = p (смотри уравнение (11) в [14]). Тогда при α = π /4 и n – m = l пучок ЭЛГ с коэффициентами (18) преобразуется в пучок Лагерра– Гаусса с топологическим зарядом l и максимальным ОУМ, равным J z / W = l .

2. Моделирование

На рис. 1 показаны распределения интенсивности и фазы двух структурно-устойчивых суперпозиций пучков ЭГ (1) с квазислучайными весовыми коэффициентами.

Рис.1. Распределения интенсивности (а-в, ж-и)

и фазы (г-е, к-м) суперпозиций пучков Эрмита–Гаусса (1) и (3) со случайными весовыми коэффициентами при следующих параметрах: длина волны λ = 532 нм, радиус перетяжки Гауссова пучка w = 0,5 мм, суммарный порядок полиномов Эрмита N = 3, расстояния вдоль оптической оси z = 0 (начальная плоскость) (а, г, ж, к), z = z 0 (зона дифракции Френеля)(б, д, з, л) и z = 2z 0 (дальняя зона) (в, е, и, м); весовые коэффициенты C p = [0,77; 0,62i; – 0,23;

– 0,44i] (а-е) и C p = [0,55; 0,63i; – 0,84; – 0,07i] (ж-м). Топологический заряд рассчитывался вдоль пунктирной окружности

Из рис. 1 видно, что оба пучка при распространении сохраняют форму своего поперечного сечения интенсивности. Теоретическое значение ОУМ (9) пучка с рис. 1 а - е равно 1,4452. Численно по формулам (5) и (6) получены значения 1,4451 (для всех трёх поперечных плоскостей). Теоретическое значение ОУМ пучка с рис. 1 ж - м равно 2,2466. Численно получены значения 2,2463 (для всех трёх поперечных плоскостей). Топологический заряд рассчитывался по формуле Берри [16] и на рис. 1 а - е оказался равен TC =–1, а на рис. 1 ж - м – TC =3.

Заметим, что в случайных весовых коэффициентах фаза каждого из них отличается от фазы предыдущего на π /2. Если сделать задержку фазы равной – π /2, то ТЗ станет равным соответственно +1 и –3.

Из этих численных примеров видно, что максимальный по модулю ТЗ, который может быть у пучка (1), равен номеру N или – N , в сумме (1). При этом нормированный ОУМ меньше N .

Заключение

В работе получено общее выражение в виде конечной суммы для ОУМ структурно-стабильного поля, из которого следует, что отличный ОУМ у такого светового поля будет в случае, если хотя бы один из двух соседних коэффициентов в конечной сумме, состоящей из функций ЭГ, будет комплексный. Показано, что если число слагаемых в сумме из функций ЭГ четное и отличные от нуля коэффициенты есть только у двух соседних центральных слагаемых и одно из них чисто мнимое, а другое действительное, то ОУМ может быть равен половине полного числа слагаемых в сумме. Если коэффициенты в сумме выбраны как биномиальные коэффициенты, то ОУМ пучка может достигать максимума и быть равным полному числу слагаемых в сумме.

Работа выполнена при поддержке Российского научного фонда (грант 18-19-00595) в части «Орбитальный угловой момент», а также Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН в части «Моделирование».