Орбитальный угловой момент суперпозиции двух обобщённых лазерных пучков Эрмита–Гаусса

В 1992 L. Allen [1] показал, что моды Лагерра– Гаусса (ЛГ) обладают орбитальным угловым моментом. Таким же моментом обладают все оптические вихри или сингулярные лазерные пучки с фазовой особенностью или дислокацией волнового фронта [2]. У таких пучков вектор Умова– Пойнтинга (поток мощности) вращается по спирали вокруг точек фазовой сингулярности. Первая генерация лазерного пучка с фазовой сингулярностью была осуществлена в 1979 году [3]. Было показано, что две моды Эрмита–Гаусса HG 01 и HG 10 , складываясь интерференционно в резонаторе криптонового ионного лазера, формируют моду ЛГ LG 01 . В 1989 году в работе [4] был введён термин «оптический вихрь» (optical vortex). В 1990 году М.С. Соскин [5] cформировал оптический вихрь с помощью амплитудной дифракционной решётки с «вилкой», а в 1992 году сингулярный лазерный пучок был сформирован с помощью спиральной фазовой пластинки [6].

В 1991 году В.Г. Волостников с помощью астигматического модового конвертора преобразовал моду ЭГ высокого порядка в моду ЛГ, обладающую фазовой сингулярностью [7]. В [8] был рассмотрен интерференционный модовый π/2-конвертор. Орбитальный угловой момент лазерных пучков используется для вращения микрочастиц, в квантовой телекоммуникации, микроскопии, интерферометрии, метрологии и т.д. Современный обзор по ОУМ для света можно найти в [9]. Также многие применения вихревых лазерных пучков с ОУМ описаны в монографии [10]. Формированию оптических вихрей с помощью интерферометров посвящены работы [11 – 13]. В этих работах с помощью интерференции трёх плоских волн сформирована матрица оптических вихрей.

В [7] получена формула, позволяющая получить моду ЛГ как конечную сумму мод ЭГ. Например, для того чтобы получить моду ЛГ с топологическим зарядом 2, требуется сложить минимум три моды ЭГ с определёнными комплексными коэффициентами. В этой работе мы покажем, что можно получить световое по- ле с любым целым ОУМ, сложив только две моды ЭГ с определёнными номерами.

Заметим, что недавно с помощью алюминиевого отражающего дифракционного оптического элемента был сформирован лазерный оптический вихрь с наибольшим ОУМ и наибольшим топологическим зарядом, равным 5050 [14]. Известны различные методы формирования лазерных пучков с дробным ОУМ [15–17]. В [15] c помощью линейной комбинации мод ЛГ формировались лазерные пучки с полуцелым ОУМ. В [16] c помощью астигматического модового конвертора формировались пучки Эрмита–Лагерра– Гаусса, обладающие дробным ОУМ. В [17] c помощью конической дифракции гауссова пучка с круговой поляризацией формировался пучок Бесселя с ОУМ, меньшим единицы.

В данной работе рассчитан ОУМ для линейной комбинации из двух пучков ЭГ, двойные номера которых состоят из прямых и переставленных местами соседних целых чисел и которые (пучки) смещены по фазе друг по отношению к другу на π/2. Причём рассматриваются обобщённые пучки ЭГ, которые при определённых параметрах переходят в моды ЭГ и в элегантные пучки ЭГ. Показано, что модуль ОУМ для двух соответствующих мод ЭГ является целым числом, а модуль ОУМ для двух элегантных пучков ЭГ всегда равен единице. При сложении двух соответствующих гибридных пучков ЭГ модуль ОУМ всегда будет дробным числом. Исключением является тривиальный случай, когда складываются два обобщённых пучка ЭГ с номерами (0, 1) и (1, 0). В этом случае, как и для мод ЭГ, модуль ОУМ равен 1.

1. Обобщённые лазерные пучки Эрмита–Гаусса

Моды Эрмита–Гаусса известны в оптике давно [18]. Элегантные пучки ЭГ описываются функциями с комплексным аргументом. Эти пучки впервые рассмотрел в 1973 году A.E. Siegman [19].

Однако имеются пучки ЭГ, которые также являются решением параксиального уравнения распространения и имеют явный аналитический вид. Эти пучки при определённых параметрах переходят в моды ЭГ [18] и элегантные пучки ЭГ [19].

Рассмотрим комплексную амплитуду света в начальной плоскости z =0 вида E nm ( x , y ) = E 1 ( x ) E 2 ( y ), где

E 1 ( x ) = exp [–( x / a )²] H n ( x / b ) и

E2(y) =exp[–(y/c)2] Hm(y/d), где a, b, c, d – действительные числа. Так как ком-

плексная амплитуда является произведением двух функций, зависящих от разных декартовых координат, то распространение всего 2D пучка можно рассматривать как распространение 1D пучка по любой из поперечных координат. Комплексная амплитуда такого 1D светового поля на расстоянии z в параксиальном приближении вычисляется с помощью преобразования Френеля и равна:

где q ( z ) = (1 + iz / z 0 )^1/2. Заметим, что обобщённые (1) и элегантные (4) пучки ЭГ не являются модами свободного пространства и при распространении изменяют структуру поперечного распределения интенсивности. Понятно, что двумерные обобщённые пучки ЭГ образуются путём перемножения соответствующих функций (1), (3) и (4). Можно сформировать гибридный пучок ЭГ, который по одной координате будет являться модой ЭГ, а по другой декартовой координате – элегантным пучком ЭГ:

E h ( x , У , z = o ) = exp

x

a

y

1/2

I - iz„ 1

E 1 ( x , z ) = || i x

V z J

x

—

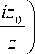
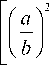
1 + z

n /2

где

x H

m

2xx )

Hn a

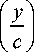
x exp

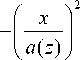
ka ²

2,

a ( z ) = a

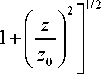
R ( z ) = z

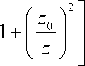
b ( z ) = b I — Il 1 — V ^z o J V

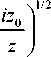
ikx ²

+--

2 R ( z )

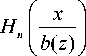
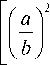
1 + z

1/2

.

z

Для комплексной амплитуды E ₂ ( y , z ) можно получить выражения, аналогичные (1) и (2), заменив x, n, a, b на y, m, c, d соответственно.

Из (1), (2) при a/b = c/d = 2 следует хорошо известное выражение для мод ЭГ:

E n ( x , ^z ) = i n

a      ^2x

a(z)] n [a(z).

x exp

x ²       ikx ²

a2 (z) 2 R (z)

— i ( n + 12 ) arctg | — V ^z o

В двумерном случае одномерные моды (3) перемножаются и получается двумерная мода ЭГ E nm ( x , y , z )= E n ( x , z ) E m ( y , z ).

Если выполняется условие, что a/b = c/d = 1, то вместо (1), (2) получим выражение для элегантных мод ЭГ [19]:

n +1

^Ee ⁽ x , ^z ) = ( q ^{( z} )K^v exp

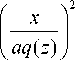
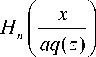
Пучки ЭГ (1) не имеют ОУМ. Линейная комбинация пучков ЭГ с действительными коэффициентами тоже будет иметь ОУМ, равный нулю. Отличным от нуля ОУМ может быть только для линейной комбинации пучков ЭГ с комплексными коэффициентами. В следующих разделах будет рассчитан ОУМ для суперпозиции из двух обобщённых пучков ЭГ с задержкой по фазе на π /2.

2. Орбитальный угловой момент линейной комбинации двух мод Эрмита–Гаусса

Пусть в начальной плоскости задана комплексная амплитуда света:

E ( x , У ,0 ) = exp

2 w у^{( x +} У )

x

^x f H 2 p ( cx ) H 2 s +1 ( СУ ) ⁺ i Y H 2 s +1 ( cx ) H 2 p ( СУ ) ] ,

где w, c, γ – действительные числа. Найдём ОУМ такого пучка по формуле [20]:

Jz =H E *

ℝ2

dEd xy — dyd

d x d y .

Строго говоря, в (7) показан не весь ОУМ, а только его проекция, определённая с точностью до константы, на оптическую ось, которая усреднена по поперечной плоскости. ОУМ (7) сохраняется по мере распространения пучка [20], и поэтому его можно вычислять в любой плоскости, например, при z = 0. Подставив (6) в (7), получим:

+x

J_z = 4 i y c j x exp ( — w ² x ² ) H _{2 p} ( cx ) H ₂ s _{+ 1} ( cx ) d x x

-да

x

+да

² P j exp ( ^- w ² У ² ) H 2 s +1 ( cy ) H 2 p -1 ( cy ) ^d У -

-да

+да                                               _]

^— ( ² s ⁺ 1 ) j exp ( ^— w ² У ² ) H 2 p ( cy ) H 2 s ( cy ) ^d У .

-да                                                        _

Так как в (8) под интегралами стоят многочлены, то интегралы можно вычислить и представить их через конечные суммы:

4 i лу[ ( 2 p ) ! ( 2 5 + 1 ) ! ]

J z =----

w ⁴ p ^{+ 5 + 1 )}

X

пример, при γ = 1/2 ОУМ (12) будет целым числом при p =2: J z / I =–4 i , при p =7: J z / I = –12 i и т.д.

Для линейной комбинации мод ЭГ вида

mi"^ ^{5 + 1 )} [ ( 5 + 1 ) c ² - kw ² ] (,

k =0

c ² - w ² ) p ^{+ 5} -2 ^k ( 2 c ² ) 2 ^k

( p - k ) ! ( 5 + 1 - k ) ! ( 2 k ) !

X

E ( x , y ,0 ) = exp

2 w

^- T^{( x +} y )

X

min ( ⁵ , p -i ) ( 2 c ² )     (

X Z

k =0

min ( p , 5 )

- Z k=0

• ~       ~ \ p + 5 - 2 k -1

. c ^- w )

( p - 1 - k ) ! ( 5 - k ) ! ( 2 k + 1 ) !

-

^{x[ H}n ( ^wx ) ^Hn +1 ( wy ) ⁺ i Y ^Hn +1 ( ^wx ) ^Hn ( wy ) ]

аналогично (14) можно получить нормированный ОУМ для любого целого n :

( 2 c² ) 2 ^k ( c² - w² ) p ^{+ 5} -2 ^k ( p - k ) ! ( 5 - k ) ! ( 2 k ) !

J z _ 2 i y ( n + 1) 7 ⁼ " Y

Выражение (9) громоздко, и из него трудно заключить, когда ОУМ будет целым, когда дробным и когда равен нулю. Можно только сделать определённые выводы при некоторых условиях. Например, если p >  s , c = w + 5, 5<< w , то при условии (p - c )(2 5 + 1) ¹ w > 5 в (9) Im( J z )>0. Если в (9) c = w , все суммы пропадают и остаются только слагаемые с максимальным номером k . Из (6) видно, что при c = w складываются две моды ЭГ с переставленными номерами. Из ортогональности мод ЭГ следует, что отличный от нуля ОУМ будет только для линейной комбинации мод с двумя последовательными номерами, то есть когда p = s . В этом случае вместо (9) получим:

2^{4 p + 2} i луГ ( 2 p + 1 ) ! l 2

J z =--•                      (10)

w ²

Для того чтобы ОУМ не зависел от мощности лазерного излучения, рассмотрим нормированный на интенсивность ОУМ. Мощность пучка (6) описывается выражением ( c = w , p = s ):

„             n ( 1 + y ² )

I = Д E*E d x d y = ^v 2 ² 2¹⁺⁴ p ( 2 p ) ! ( 2 p + 1 ) !. (11) ℝ ^{2                w}

Поэтому нормированный ОУМ (ОУМ, делённый на мощность пучка) для линейной комбинации двух мод ЭГ с переставленными соседними номерами равен:

7 ="( 2)² p ^{+ 1)1}                     (¹²⁾

Из (12) следует, что при γ = 1 ОУМ линейной комбинации двух мод ЭГ

^En , n +1 ( ^x , У ) = exp

2 w

^- у^{( x +} У )

X

^X [ ^H 2 p ( w ^X ) H 2 p +1 ( wy ) ^{+ iH} 2 p +1 ( w ^X ) H 2 p ( wy ) ]

равен по модулю целому числу:

J^ = - i ( 2 p + 1 ) .                                (14)

Заметим, что при некоторых значениях p ОУМ будет равен целому числу и при значениях γ≠ 1. На-

Заметим, что из-за того, что сумма номеров обеих мод в (15) одинакова, линейная комбинация (15) также будет являться модой (фазы Гоу ( m + n + 1)arctg ( z / z ₀ ) у обоих мод тоже одинаковые) и при распространении будет сохранять свой вид, меняясь только масштабно. Получается интересный результат: мода (15) обладает ОУМ, то есть вектор Умова–Пойнтинга локально описывает спираль в пространстве вдоль оптической оси, но пучок при этом не вращается, а распространяется без изменения своей структуры.

На практике пучок (6) или (15) при c = w можно сформировать с помощью интерферометра Маха– Цендера. Мода ЭГ E nm ( x , y ), сформированная на выходе из лазера, разделяется 50%-зеркалом на два одинаковых пучка, которые попадают в разные плечи интерферометра. В одном из плеч интерферометра с помощью призмы Дове мода ЭГ поворачивается на 90 градусов E_mn ( x , y ). На выходе из интерферометра обе моды совмещаются в один пучок с относительной задержкой по фазе на π/2.

3. Орбитальный угловой момент линейной комбинации двух элегантных пучков Эрмита–Гаусса

Рассчитаем ОУМ для линейной комбинации двух элегантных пучков ЭГ. Для этого в (6) положим c = w / V2 и p = 5 , получим:

E e ( x , у ) = exp

2 w

^- у^{( x + y} )

X

X

„ I wx 1.. I wy I

HJ    I H _, I    1 +

⁺ i Y H 2 p +1

wx

H 2 p

wy

Тогда нормированный ОУМ, аналогичный (12), будет иметь вид:

Jz I

I 2 i y 1

.

( 1 + y ² J

Из (18) видно, что линейная комбинация двух элегантных пучков ЭГ (17) будет всегда обладать ОУМ,

равным по модулю 1 (при γ= 1) при всех возможных

значениях номеров p .

Это очень неожиданный результат. Получается так, что ОУМ (14) для двух мод ЭГ определяется максимальным номером моды, участвующей в линейной комбинации. И поэтому чем выше номер моды ЭГ, тем больше ОУМ лазерного пучка (13). Для элегантных пучков (17) из (18) следует, что ОУМ оп-

Тогда нормированный ОУМ для пучка (22) будет иметь вид:

J = I 2iу | (2p +1)!

I   ( 1 + y ² J ( 4 p - 1 ) !!'

ределяется разностью двух номеров пучка, участвующих в линейной комбинации. А так как разность номеров пучков в (17) равна единице, то и ОУМ равен по модулю 1 (при γ= 1).

Для линейной комбинации элегантных мод с другими номерами (пусть k = 2 l + 1 – нечётное)

E e ( x , y ) = exp

2 w

— у (x + У )

X

X

H 2 p

wx I I wy ^ IH 2 p+k I ^

Так как в (23) в числителе из-за (2 p + 1)! всегда будут чётные и нечётные сомножители, а в знаменателе из-за (4 p – 1)!! всегда будут только нечётные сомножители, то ОУМ (23) при γ = 1 никогда не будет целым числом, кроме тривиального случая: γ= 1 и р =0. Например, при p =2 и γ= 1 из (23) получим J_z / I = i 8/7. Этот ОУМ по модулю немного больше единицы. Заметим также, что ОУМ из (23) имеет противоположный знак по отношению ко всем предыдущим рассчитанным ОУМ.

В другом случае, когда в сумме двух гибридных пучков ЭГ мода ЭГ имеет меньший номер, чем элегантный пучок ЭГ:

^Eh 2 ( x , У ) = exP

^{+ 1} Y H 2 p + k

wx

H 2 p

wy

2 w

- у(x + У )

получим ОУМ в виде

J_L = — J13 k (4 p + k ) Г ²(2 p + k /2)       ₍₂₀₎

I ( 1 + y ² Jr (2 p + 1/2) Г (2 p + k + 1/2), ¹ ’

где Г( x ) – гамма-функция. Выражение (20) совпадает с (18) при k = 1. При следующем номере k = 3 из (20) следует:

Jz

I

I 2 i у | 3(4 p + 1) ( 1 + y ² J (4 p + 5) .

При γ= 1 и при больших p модуль ОУМ (21) близок к 3, то есть близок к разности номеров элегантного пучка ЭГ (19).

4. Орбитальный угловой момент линейной комбинации двух гибридных пучков Эрмита–Гаусса

Под гибридными пучками ЭГ здесь понимается пучок, который по одной оси является модой ЭГ, а по другой координатной оси – элегантным пучком ЭГ. При этом возможны два варианта линейной комбинации гибридных пучков.

Рассмотрим сумму двух гибридных пучков ЭГ, у которой мода ЭГ имеет больший номер, чем элегантный пучок ЭГ:

E h 1 ( ^x , У ) = ^exP

2 w

— у(x + У )

X

X

TT I wx I rr /    \

H 2 p l I H 2 p +1 ( wy ) ⁺

^{+ 1} Y ^H 2 p +1 ( wx ) ^H 2 p

^{X H} 2 p ( ^wx ) ^H 2

wy|+

, . TT I wx I TT / X ^{+ 1} Y ^H 2 p +1 I      I ^H 2 p ( wy )

вместо (23) получим другое выражение для ОУМ:

J_z _ I 2 i Y I (2 p + 1)!(2 p + 1)( p² - 1) — —

I     ( 1 + y ² J         ( 4 p + 1 ) !!

Из (25) также следует, что ОУМ для пучка (24) всегда будет дробным числом, кроме тривиального случая: γ = 1 и р =0. Например, при p = 2 и γ= 1 из (25) получим J z / I = – i 40/21. Этот ОУМ по модулю немного меньше двойки. Заметим, что во всех рассмотренных случаях смена знака у параметра γ приводит к смене знака ОУМ. Заметим также, что общий сомножитель в (12), (18), (21), (23) и (24) 2γ /(1 + γ²) всегда меньше или равен единице.

5. Численное моделирование

Для моделирования рассмотрим линейную комбинацию двух обобщённых пучков ЭГ. Пусть в начальной плоскости ( z =0) световое поле имеет комплексную амплитуду

77/               I x + У I

E(x,у,0) — exp|--у |х

I w J

^X [ ^H 2 p ( bx ) ^H 2 _s +1 ( cy ) ^{+ 1} Y ^H 2 _s +1 ( cx ) ^H 2 p ( by ) ] -

Интенсивность такого светового пучка при длине волны X и значениях параметров p = 5 = 2 (т.е. используются полиномы Эрмита 4-й и 5-й степени) в начальной плоскости (в области -10 X <  x < 10 X , -10 X <  x < 10 X ) для некоторых значений масштабирующих множителей b и c показана на рис. 1 –4.

а)

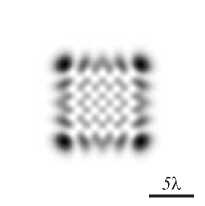
Рис. 1. Интенсивность пучка (26) без несущей частоты (а) и с несущей частотой (б) для значений параметров: w = 2X, b = c = 22/w (две моды ЭГ)

б)

Рис. 2. Интенсивность пучка (26) без несущей частоты (а) и с несущей частотой (б) для значений параметров: w = 2X, b = c = 1^w (два элегантных пучка ЭГ)

Рис. 3. Интенсивность пучка (26) без несущей частоты (а) и с несущей частотой (б) для значений параметров: w = 2X, b = 1/(7X), c = 1/(3X) (два обобщённых пучка ЭГ с разной шириной по осям)

б)

Рис. 4. Интенсивность пучка (26) без несущей частоты (а) и с несущей частотой (б) для значений параметров: w = 2X, b = 1/(5X), c = 1/(5X) (два обобщённых пучка ЭГ с одинаковой шириной по осям)

б)

На рис. 1 б –4 б показана интенсивность пучков (26), когерентно сложенных с наклонной плоской волной:

I ( x , y , z = 0) = | E ( x , y ,0) + C exp( i a x )|2,           (27)

где амплитуда C и пространственная частота a подбирались для лучшей наглядности картин на рис. 1–4. На рис. 1 б –4 б видны характерные «вилочки» среди интерференционных полос, в точке разветвления которых находятся изолированные нули интенсивности и фазовые сингулярности. Модули ОУМ для пучков равны: 5 (рис. 1 а ), 1 (рис. 2 а ), 0,95 (рис. 3 а ) и 0,92 (рис. 4 а ).

Заключение

В работе получены следующие результаты.

– Получено выражение для комплексной амплитуды обобщённых параксиальных пучков Эрмита– Гаусса (1). При определённых параметрах эти пучки переходят в известные моды ЭГ и элегантные пучки ЭГ.

– Рассчитан орбитальный угловой момент (ОУМ) линейной комбинации двух обобщённых пучков ЭГ с двойными номерами (в прямом и обратном порядке) из двух соседних целых чисел и с задержкой по фазе на π/2.

– Показано, что модуль ОУМ для суммы таких двух мод ЭГ – целое число, пропорциональное максимальному номеру моды ЭГ, для суммы двух элегантных пучков ЭГ – всегда единица, для суммы двух гибридных пучков ЭГ – дробное число.

Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации, ФЦП «Научные и научно-педагогические кадры инновационной России» (соглашение № 8027), грантов Президента РФ поддержки ведущих научных школ (НШ-4128.2012.9), молодого кандидата наук (МК-3912.2012.2) и молодого доктора наук (МД-1929.2013.2), а также грантов РФФИ (12-07-00269, 1207-31117, 13-07-97008).