Ординация пресноводных сообществ на основе анализа нечетких множеств

И дея использовать нечеткие множества (fuzzy sets) и нечеткую логику (fuzzy logic) появилась как эффективная практическая мера преодоления принципа несовместимости Неймана–Заде: «…повышение точности описания сложной системы становится несовместимым со здравым смыслом, поскольку сложность модели становится соизмеримой со сложностью самого объекта» [1, 2]. Впоследствие Б. Коско [3] доказал теорему о нечеткой аппроксимации (FAT), согласно которой применение элементарных логических высказываний и нечеткой формализации позволяет сколь угодно точно отразить произвольную взаимосвязь «вход-выход» без использования традиционного сложного математического аппарата. С конца 80-х годов, после бурного развития технических устройств на базе нечетких контроллеров и экспертных систем, концепция нечетких множеств стала важным обобщением классических математических теорий и неотъемлемой составной частью современных систем искусственного интеллекта.

Основные понятия нечетких множеств, впервые сформулированные американским ученым Лотфи Заде [1, 4], сводятся к следующему. Универсальное множество С является нечетким, если для его элементов x существует функция принадлежности (membership function) µ С ( x ), принимающая на этом множестве значения в интервале от 0 до 1: µ С ( x ) = 0 означает полную несовместимость, т.е. x ∉ С , a µ С ( x ) = 1 – истинную принадлежность, или x ∈ С. Нечеткое множество С задается множеством упорядоченных пар типа C = { x , µ С ( x )}; в частном случае, если функция принадлежности принимает значение только 0 или 1, то C становится «четким» или обычным множеством. Оценка степени сродства (grade) каждого произвольного анализируемого объекта x множеству С и конструирование функ-

ции µ С ( x ) осуществляется на основе экспертных заключений, либо подходящего формального метода обработки исходных данных.

Традиционные принципы анализа структуры сообщества и формирования эколого-ценотических групп предполагают, что выделяемые классы видов или местообитаний представляют собой детерминированные совокупности: т.е. каждый объект может принадлежать только к одному таксону. Результат четкой кластеризации представляет собой характеристическую матрицу U = [ ϕ ki ], ϕ ki ∈ {0, 1}, где каждый элемент равен 1, если объект x i принадлежит кластеру A k , или 0 в противном случае . Ограниченность такого подхода проявляется, например, при неизбежной трансгрессии отдельных видов в «непредназначенные» для них ареалы, что приводит к аналитической неопределенности и множественности выводов при сравнении сообществ.

Разумной альтернативой понятию абсолютной дискретности в классической таксономии является интерпретация компонентов экосистем как нечетких объектов в составе гибко настраиваемых орди-национных структур. Единственным отличием матрицы нечеткого разбиения F = [ µ ki ], µ ki ∈ [0, 1], от матрицы U является то, что метрика µ ki задает в масштабе от 0 до 1 непрерывную функцию принадлежности объекта x i (вида или местообитания) к каждому из выделенных классов A k , k = 1, 2, …, c . Расчет компонентов F с учетом минимизации критерия разброса может быть выполнен с использованием одного из алгоритмов нечетких C -средних (см. метод неопределенных множителей Лагранжа, процедуру Густавсона-Кесселя, «горный» алгоритм Ягера–Филева в монографии [5]).

Результаты использования алгоритмов нечетких множеств в биогеографии, экологии и численной систематике имеют давнюю историю [4, 6-12]. Предпринимались даже попытки представить новую концептуальную основу, объединяющую нечеткую математику и динамическую теорию систем, которая «позволит в математически строгой и экологически глубокой манере идентифицировать природу взаимодействия между ключевыми ком- понентами экосистем в гиперпространстве значимых факторов» [7]. Однако отсутствие стандартных методик конструирования нечетких экосистем не всегда приводили к повышению точности вычислений по сравнению с существующими вероятностными методами.

В наибольшей мере преимущества математики нечетких множеств были реализованы в методе ординации сообществ, разработанным Д. Робертсом [6, 11] и известном под аббревиатурой FSO (Fuzzy Sets Ordination). Метод использует данные о факторах окружающей среды непосредственно при проведении вычислений и относится к семейству процедур прямой ординации, таких как канонический анализ соответствия CCA или канонический анализ главных координат CAPC, которые, в свою очередь, основаны на линейной алгебре и геометрических представлениях [13].

Практически с использованием метода FSO моделируется распределение оптимумов относительной таксономической насыщенности разных местообитаний на шкале градиента фактора среды, т.е. оценивалась роль, которую играет переменная z в формировании или ограничении видовых композиций сообщества. Эта аналитическая процедура представлена К. тер Брааком [13, глава 4] как «калибровка».

Задачей калибровки является использование для экологической экспертизы целостных таксономических композиций сообществ на участках, включая как относительно редкие виды-биоиндикаторы, так и виды с более широкими экологическими амплитудами. Теоретической основой разработки конкретных дефиниций такого многомерного отклика является модель совместного распределения видов (species packing model), основанная на концепциях максимального правдоподобия и учитывающая различное положение экологических оп-тимумов каждого вида на шкале градиента фактора среды. Практически оценка отклика сводится к обоснованию различных полуколичественных биотических индексов, использующих, как правило, алгоритм среднего взвешивания или обратную регрессию [13]. Функцию принадлежности µ E ( x ) можно рассматривать как одну из версий количественного представления мультивидового отклика, оценивающего на интервале [0, 1] приведенную таксономическую изменчивость при различных значениях фактора среды z.

В настоящей статье представлены результаты ординации донных сообществ по продольному градиенту средней равнинной реки и обсуждаются достоинства и недостатки метода FSO по сравнению с широко используемым CCA-анализом.

МАТЕРИАЛ И МЕТОДИКА

Исходными данными для ординационного анализа явились результаты многолетней гидробиологической съемки, проведенной на станциях наблюдения, расположенных на всем протяжении рек Сок и Байтуган. Река Сок является не зарегулированной равнинной рекой II-IV класса качества (длина 375 км), берущей начало в отрогах Бугульминско-Белебеевской возвышенности и впадающей в Саратовское водохранилище выше г. Самара. Река Байтуган (22 км) относится к рекам предгорного типа, впадает в р. Сок в верхней его части, имеет родниковое питание и по качеству вод относится к эталонным водотокам региона.

Объектом исследований явились сообщества макрозообентоса, которые обладают признанными биоиндикационными свойствами и являются наиболее стабильным и разнообразным компонентом лотических экосистем [14-15]. Всего по результатам 147 гидробиологических проб в исходные таблицы было включено 214 видов и таксономических групп бентоса, которые встретились в 3 или более выборках из разных местообитаний.

С учетом гидрологических характеристик водотоков речная система была разделена на 13 экологически однородных участков (в том числе 4 участка в пределах р. Байтуган), включающих примерно одинаковое количество проб от 10 до 14. Таксономический состав макрозообентоса на участках оценивался по трем показателям: видовое богатство, частота встречаемости в пробах и средняя прологарифмированная численность особей каждого вида. Для оценки влияния факторов среды использовались среднемедианные значения гидрологических и гидрохимических показателей для каждого участка, а также их биотопические характеристики.

В общем случае механизм нечеткого логического вывода включает четыре этапа: введение нечеткости (фазификация), нечеткий вывод, композиция и приведение к четкости (дефазификация). На первом этапе метод FSO переводит данные экологического мониторинга в нечеткое топологическое пространство, где элементы связаны между собой на интервале [0, 1] функцией принадлежности ц . Рефлексивная и симметричная матрица любых мер подобия является примером такого нечеткого отношения близости между каждой парой элементов. На основании рекомендаций Р. Бойса и П. Элисона [9], рассмотревших множество индексов сходства на предмет их применения в FSO, нами использовался индекс Горна, дающий наиболее стабильные результаты для количественных признаков:

a

zk=/ tk+j )iog(t.+j) -zk=1 tk log tk-^k=1 tjk log tjk ij

SS      SS     S     SS     s k=1 ik      k=1 jk og    k=1 ik      k=1 jk        k=1 ik og   k=1 ik      k=1 jk og   k=1 jk где tik – частота встречаемости вида k (k = 1, …, S) в гидробиологических пробах, взятых на i-м участ- ке. Меры подобия были трансформированы в меры расстояния: dij = (1– aij).

Расчет компонентов нечетких множеств выполнялся на основе двух таблиц исходных данных: матрицы Z факторов среды для каждого из 13 участков водотока и симметричной матрицы D экологических расстояний Горна между этими биотопами. В случае одномерного FSO нами поочередно задавался один ключевой параметр среды z , который потенциально может оказаться ведущим градиентом. После этого реализовывалась последовательность операций на промежуточных множествах

µE(x) = {1 + [1 - µG(x)]2 – [1 – µC(x)]2}/2; µ (x)= где x и y – анализируемые экологические объекты (участки речной экосистемы); d(x,y) – сходство между этими объектами в соответствии с выбранной метрикой; µP(x), – функции принадлежности, задающие каждое из представленных нечетких множеств, P = {x, µP(x)}, P = E, C, G; µA(x) – набор нормированных значений фактора среды zx для всех классифицируемых объектов x: µ (x)= zx -min(z) .

^A      max( z ) - min( z )

Одномерный FSO, как и одномерный регрессионный анализ, позволяет оценить статистическую зависимость функций принадлежности размытых множеств только от одного фактора среды. Для анализа совместного влияния всего комплекса переменных была использована многомерная версия ординации нечетких множеств MFSO [11]. Для определения нечетких множеств в многомерном пространстве сначала выполнялось нахождение орди-национной оси относительно экологической переменной, которая в наибольшей мере объясняет вариацию композиций видов (т.е. имеет наибольший коэффициент корреляции). Вторая ось, связанная со следующим фактором, рассчитывалась как перпендикуляр к первой с использованием процедуры ортогонализации Грамма-Шмидта, а ее значения соответствовали остаткам регрессии на первую ось. Таким образом, второй градиент нечеткого множества соответствовал только той доле влияния второй переменной, которая не может быть объяснена первым фактором. Оси третьего и высших порядков, отражающие долю таксономической вариации, не связанную со всеми предыдущими осями нечет- кого множества, рассчитывали аналогично.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Многомерная ординация экологических сообществ, выполненная методом канонического анализа соответствий (CCA – Canonical Correspondence Analysis), позволила одновременно провести анализ распределений видов и местообитаний относительно векторов градиента факторов среды и эффективно представить графически полученные результаты на обобщенной ординационной диаграмме (рис. 1). Анализ совокупности из 12 различных

[6, 10], позволяющая преобразовать конфигурацию точек из нечеткого топологического пространства в евклидово пространство, где становятся доступными средства параметрической статистики.

Результирующее нечеткое множество E вычислялось с использованием оператора антикомму-тативной разности , оценивающего контраст двух полярных нечетких множеств C и G , соответствующих высоким и низким значениям изучаемого фактора среды z :

∑ _d ( _xy ) µ _A ( _x )           ∑ d ( xy )[1 - µ _A ( x )]

^{y ≠ x              ;} µ _G ( x ) = ^{y ≠ x                     ,}

∑ µ _A ( y )                ∑ [1 - µ _A ( y )]

• y ≠ x                                y ≠ x

гидрологических, геоморфологических и гидрохимических факторов среды в бассейне рек Байтуган– Сок показывает, что первая главная ось ординации, объясняющая 34,4% вариации данных, тесно связана с пространственным градиентом природных условий и объединяет высоту над уровнем моря, глубину и температуру воды в месте отбора проб, изменчивость состава грунтов и большинство гидрохимических показателей.

На рис. 1 можно выделить следующие характерные «зоны» водотока и соответствующие им группы видов макрозообентоса, подтвержденные результатами специальных гидробиологических исследований [15]:

• 1.    Река Байтуган (участки В_01 – B_08) с большим числом родников, каменистым субстратом и высоким содержанием кислорода), где основу донных сообществ составляют реобионтные и оксибионтные виды, характерные для «эталонно чистых» биотопов.

• 2.    Верхнее течение р. Сок (участки S_01 – S_02 с песчано-галечным субстратом и относительно чистой водой), где видовой состав макрозообентоса является типичным для «ритрали» водотоков, а основную долю фаунистического разнообразия составляют относительно немногочисленные таксоны литореофильных личинок амфибио-тических насекомых Diptera, Ephemeroptera, Trichoptera.

• 3.    Промежуточная «зона» р. Сок (участки S_03 – S_05), где происходит сукцессионая смена экоформ и видовая структура донных сообществ существенно изменяется за счет развития эвриби-онтных таксонов.

• 4.    Среднее течение р. Сок (участки Ѕ_08 – Ѕ_09 со смешанными грунтами, относительно высоким уровнем органического загрязнения и низким содержанием кислорода), представленное различными по своим аутэкологическим характеристикам эвритопными и эвриоксибионтными таксонами.

• 5.    Приустьевые участки (S_12 – S_13) с илистым дном, относительно высоким содержанием биогенных элементов, но достаточной концентрацией кислорода, где происходит развитие лимно-фильных моллюсков, пелофильных хирономид и

• ракообразных, обусловленное трансформацией р. Сок водами Саратовского водохранилища.

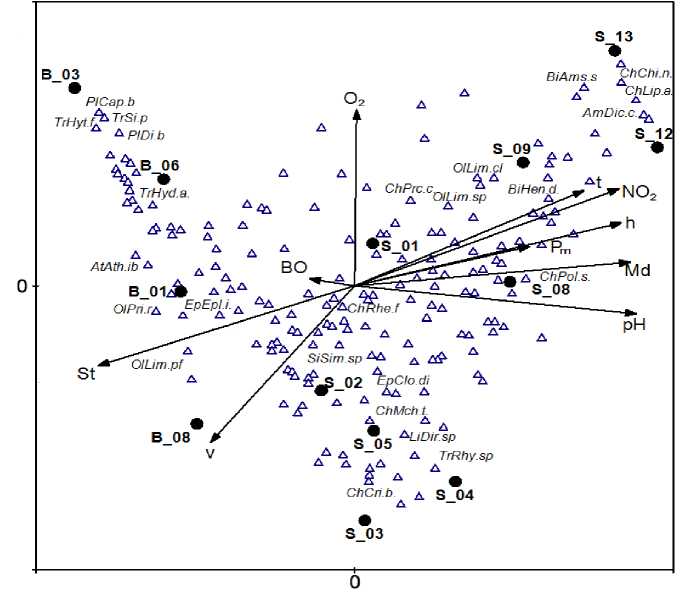
Рис. 1. Совмещенная ординационная диаграмма участков и видовой структуры сообществ макрозообентоса экосистемы рр. Байтуган-Сок с использованием канонического анализа соответствий CCA:

v – скорость течения, t – температура, h – глубина в местах отбора проб, pH – активная реакция среды, BO – бихроматная окисляемость, NO 2 – нитритный азот, О 2 – кислород, P m – фосфор минеральный, St – каменистость грунта, Md – заиленность грунта; AmDic.c. – Dikerogammarus caspius , AtAth.ib – Atherix ibis , BiAms.s – Amesoda scaldiana , BiHen.d. – Henslowiana dupuiana , ChChi.n. – Chironomus nudiventris , ChCri.b . – Cricotopus bicinctus , ChLip.a. – Lipiniella araenicola , ChMch.t. – Microchironomus tener , ChPol.s. – Polypedilum scalenum , ChPrc.c. – Procladius choreus , ChRhe.f. – Rheocricotopus fuscipes , EpClo.di – Cloeon dipterum , EpEpl.i. – Ephemerella ignita , LiDir.sp – Dicranota sp., OlLim.cl – Limnodrilus claparedeanus , OlLim.pf – Limnodrilus profundicola , OlLim.sp – Limnodrilus sp., OlPri.r – Pristina rosea , PlCap.b – Capnia bifrons , PlDi.b – Diura bicaudata , SiSim.sp – Simulium sp., TrHyd.a. – Hydropsyche angustipennis , TrHyt.f – Hydroptila femoralis , TrRhy.sp – Rhyacophila sp., TrSi.p – Silo pallipes

а

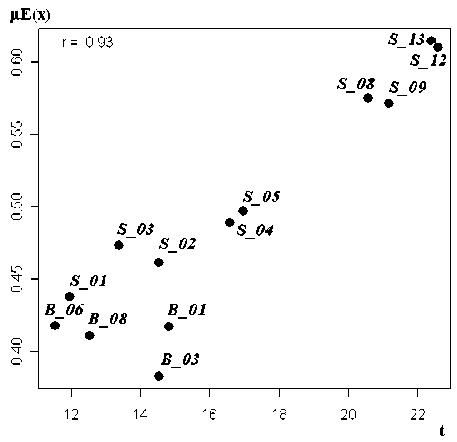
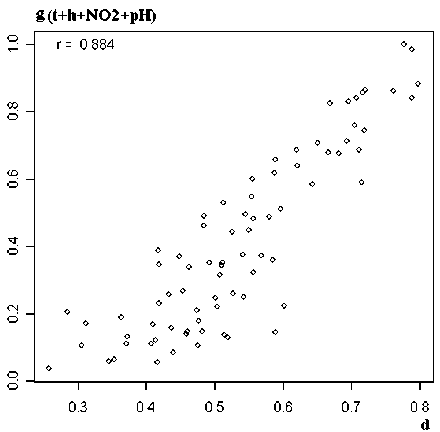
Рис. 2. Корреляционная связь функции принадлежности нечеткого множества µ E ( x ) с температурой воды t ( а ) и комплексного ординационного расстояния g (t+h+NO 2 +pH) с компонентами матрицы таксономических расстояний d ( б )

б

К сожалению, метод анализа нечетких множеств FSO в современной редакции не предоставляет таких разносторонних способов графической интерпретации, как классические алгоритмы ор-динации. Простым критерием значимости полученных осей нечетких множеств является корреляция между функцией принадлежности µE(x) и значениями соответствующей экологической переменной z и исследователю обычно предлагается проанализировать полученные корреляционные поля. На рис. 2а нетрудно заметить, что положение выделенных биотопов на шкале градиента температуры, оцененное по приведенной таксономической характерности донных сообществ, в целом совпадает с результатами CCA-ординации.

Если в распоряжении исследователя оказывается целый набор потенциальных параметров среды, определяющих закономерность распределения видов по местообитаниям, то можно последовательно провести сравнительный анализ всех факторов [10] и внешние факторы с высокой корреляцией будут считаться наиболее влияющими (табл. 1).

Таблица 1. Коэффициенты корреляции Пирсона ( r ) и Кендалла ( τ ), связывающие переменные среды с функциями µ E ( x ) принадлежности нечетких множеств (слева) и факторными нагрузками осей (справа, только для r >  ± 0,45); p n и p m – оценки статистической значимости r, найденные, соответственно, методами нормального приближения и рандомизации

Переменные среды	Метод FSO			Метод CCA
	r	p n	p m	Ось	r	τ
Температура воды (t)	0,929	4,18 ⋅ 10-6	0,001	1	0,833	0,658
Глубина в местах отбора проб (h)	0,921	7,55 ⋅ 10-6	0,001	1	0,827	0,649
Содержание нитритного азота (NO 2 )	0,828	4,72 ⋅ 10-4	0,001	1	0,744	0,763
pH	0,822	5,61 ⋅ 10-4	0,001	1	0,864	0,722
Каменистость грунта (St)	0,806	8,67 ⋅ 10-4	0,001	1	-0,805	-0,650
Высота над уровнем моря ( Н )	0,797	0,001	0,001	1	-	-
Заиленность грунта (Md)	0,778	0,0017	0,001	1	0,835	0,714
Pm – содержание минерального фосфора	0,641	0,018	0,007	1	0,582	0,348
				1	-0,450	-0,395
Скорость течения ( v )	0,412	0,16	0,077	2	-0,566	-0,369
Содержание кислорода (O 2 )	0,180	0,55	0,226	2	0,570	0,405
Площадь водосбора ( F )	0,044	0,88	0,323	1	-	-
Бихроматная окисляемость (BO)	-0,526	0,064	0,784	1	-	-

Поскольку оценки p -значений достоверности коэффициентов корреляции Пирсона r , вычисле-ные параметрическим путем нормального приближения, имеет очевидную тенденцию высокой ошибки первого рода [9], проверка статистических гипотез осуществлялась нами с использованием непараметрических процедур имитации. Для этого видовой состав всех участков экосистемы случайным образом 1000 раз перемешивался и рандомизированная оценка p соответствовала вероятности того, что имитируемый коэффициент корреляции превысит или будет равен эмпирическому значению r . Расчеты показали (табл. 1), что статистически значимым признается влияние 8 из 12 анализируемых факторов среды на таксономическую изменчивость донных сообществ. Можно также отметить тесную связь найденных коэффициентов корреляции с проекциями факторов среды на главную ось ординации, полученную нами по методу ССА.

При конструировании многомерных нечетких множеств методом MFSO вследствие применения ортогонализации Грамма–Шмидта предварительно проведится статистический анализ и тщательно исключаются те переменные среды, которые сильно коррелированны с другими факторами. В нашем случае все 8 отобранных признаков образуют сильно взаимосвязанный комплекс переменных: коэффициенты корреляции между парами статистически значимых векторов µE(x) варьируют от 0,982 до 0,999. Это подтвердилось при использовании шаговой процедуры FSO, которая оказалась полезной для быстрой селекции потенциальных осей ординации. Алгоритм стартует с фактора, имеющего наибольший коэффициент корреляции r(d, z), и последовательно включает в модель остальные переменные, оценивая их по приращению, вносимому ими в результирующее значение r.

Результаты шаговой процедуры (табл. 2 слева) позволили сразу исключить из дальнейшего рассмотрения три фактора среды, использование которых снижает общий коэффициент корреляции. Применение многомерной процедуры анализа нечетких множеств MFSO к оставшимся признакам (табл. 2 справа) дало возможность выделить две относительно некоррелированные и статистически значимые оси ординации донных сообществ, основанные на температуре воды и рН.

Считается, что «нечеткая математика обеспечивает более интуитивный подход ко многим экологическим вопросам» [6]. Действительно, в общем случае алгоритмы FSO предполагают априорный неформальный выбор параметров окружающей среды, основанный на экологических представлениях. У исследователя должны быть одна или несколько рабочих конкурирующих гипотез, которые могут быть проверены путем сравнения полученных результатов ординации на нечетких множествах. С одной стороны, это прекрасный шаг, активно включающий полевого эколога в процесс компьютерного моделирования, но вносящий, с другой стороны, определенную долю субъективизма.

Другое преимущество FSO состоит в том, что, сохраняя формальную логику и математику «четких» (евклидовых) метрик, он не зависит от каких-либо гипотетических распределений или предварительно задаваемых порогов, а основывается на нечетких функциях, оценивающих уровень принадлежности на множестве элементарных исходов.

В то же время предложенный Д. Робертсом алгоритм фазификации с использованием оператора антикоммутативной разности позволяет выделить только одну главную тенденцию в изменчивости экологических сообществ. Во многих случаях потенциальный интерес для исследователя может представлять более «объемная» картина ордина-ции сообществ в многомерном факторном про- странстве. Например, вторая главная ось на рис. 1 после «снятия» пространственной изменчивости определяет локальные флуктуации градиентов скорости течения и содержания растворенного кислорода, что позволяет легко ранжировать местообитания по этим интересным признакам. Метод FSO в нашем случае вторую и последующие шкалы полностью игнорировал.

Наконец, многомерная CCA-ординация экологических сообществ позволяет одновременно провести анализ распределений как видов, так и местообитаний относительно векторов градиента факторов среды и эффективно представить графически полученные результаты на обобщенной ординационной диаграмме (рис. 1). Средства визуализации, предлагаемые FSO, либо довольно примитивны (корреляционные поля парных взаимодействий разных нечетких множеств), либо излишне туманны для интерпретации (см. зависимость мер расстояний d от z на рис. 2б).

Несмотря на ряд отмеченных обстоятельств, использование методов нечеткой логики и других средств искусственного интеллекта представляется сегодня важной задачей экологии. Их развитие обещает как большие надежды на распутывание клубка скороспелых теоретических конструкций, так и может стать полезным инструментом в практической деятельности.

Таблица 2. Результаты шаговой процедуры селекции признаков и многомерного анализа нечетких множеств с выделением значимых осей ординации с использованием коэффициентов корреляции Пирсона ( r ); p – оценки статистической значимости приращений r, найденные методом рандомизации

Переменные среды	Шаговая процедура			Оси ординации
	r ( d , z )	Приращение	p	r (µ E ( x ), z )	Приращение	p
Температура воды ( t )	0,879			0,929		0,001
pH	0,8824	0,0034	0,07	0,9328	0,0038	0,017
Содержание нитритного азота (NO 2 )	0,8855	0,0031	0,14	0,9337	0,00095	0,055
Высота над уровнем моря ( Н )	0,8857	0,00017	0,17		-0,002
Глубина в местах отбора проб ( h )	0,8859	0,00024	0,18	0,9339	0,0002	0,071
Pm – содержание мин. фосфора	0,8859	-0,00002	0,34
Каменистость грунта (St)	0,8839	-0,002	0,23
Заиленность грунта (Md)	0,8831	-0,00079	0,25

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант № 07-04-96610) и в рамках программы Президиума РАН «Биологическое разнообразие», раздел «Динамика биоразнообразия и механизмы обеспечения устойчивости биосистем».

В расчетах использовались пакеты ординации и многомерного анализа для объектноориентированной статистической среды R, разработанные исследовательской группой Университета штата Монтана, США . Авторы благодарны ее руководителю проф. Д. Робертсу (David W. Roberts) за консультации и замечания, высказанные по ходу подготовки рукописи.