Организация мониторинга воздушного бассейна тепловой электрической станции с помощью лазерного зондирования

Для практического использования в поставленной задаче вполне применимо уравнение лазерного зондирования (УЛЗ) в приближении однократного рассеяния света на аэрозолях. Задача облегчается тем, что для примененного лазера на 2-й гармонике иттрий - алюминиевого граната (зеленый свет) практически полностью отсутствует поглощение света в атмосферных газах и аэрозолей. То есть все ослабление света зависит только от светорассеивающих свойств зондируемой среды. При таких условиях УЛЗ выглядит следующим образом:

x

P ( x ) = ^{P 0 c} τ ^{S 0} η ⋅ γ π ⋅ σ ( x )exp[ - 2 σ ( ζ ) d ζ ]                    (1)

2 ⋅ x ²                           ₀

Здесь P(x) – мощность эхо-сигнала, пришедшего на детектор лидара из точки, находящейся на расстоянии х от лидара;

• Р 0 – излученная лазером импульсная мощность;

• S 0 – площадь приемного телескопа;

• η – кпд всей оптической системы;

• σ(х) – распределенное вдоль трассы зондирования значение объемного коэффициента рассеяния излучения;

• γ π – значение индикатрисы рассеяния.

Экспоненциальный сомножитель представляет собой пропускание атмосферы по трассе от 0 до х и назад от нее до точки 0, т.е. до лидара. Если атмосфера не слишком мутная (т.е. это еще не облако и не дымовой шлейф), то этот сомножитель близок к единице.

Теоретически и экспериментально получено, что связь между массовой концентрацией гомогенного аэрозоля и коэффициентом рассеяния излучения τ имеет характер линейной регрессии:

M [ мг / м ³ ] = µ [ мг ⋅ км / м ³ ] ⋅ σ [ км ^{- 1} ]                           (2)

Коэффициент пропорциональности μ сложным образом зависит от вида функции распределения частиц по размерам. Дело в том, что величина σ связана со среднеквадратичным размером частиц, а М – со среднекубическим. Если заранее известен спектр размеров частиц, то коэффициент μ может быть рассчитан достаточно точно. Так, в [1] приведено измеренное в атмосфере промышленного центра (но не в дымах труб) р=(0,52 ± 0,34) [мг^км/м3]. Высокое значение стандартного отклонения (58%) обусловлено широким набором аэрозолей различного происхождения. Для аэрозоля с фиксированными свойствами, например дыма от источника, питаемого углем постоянного состава, этот разброс значительно уменьшается, и достоверность измерений массовой концентрации повышается.

Таким образом, в УЛЗ полезную информацию представляет объемный коэффициент рассеяния а. Он содержится в уравнении как непосредственно, так и через множитель экспоненциального ослабления сигнала. На малых расстояниях до дымового шлейфа (сотни метров при отсутствии тумана) этот множитель слабо отличается от единицы. И если ближняя к лидару граница шлейфа находится на расстоянии хь то коэффициент рассеяния дыма будет

P (xl) ' xl ст = ст( xl) = 2 ---------- (3)

P0 ' c 'т ' 50 ' П' Yn

Алгоритм прост, но требует калибровки лидара, т.е. знания величин Р0, т, S0, п. Необходимо также априорное знание индикатрисы обратного рассеяния уп. Это его уязвимые позиции.

Специально для тонких дымовых слоев может быть предложен еще один несложный алгоритм. Пренебрегая потерями излучения в атмосфере до шлейфа, запишем мощность сигнала от его ближней к лидару границы:

P ( Х 1 ) =

Po ' c'т '5 о ' П

2 ' x 2

' Yn 'ст(x 1)

Мощность сигнала от дальней границы облака при тех же условиях

P(x2) =

Po'c'т'50'П

2' x2

^x 2

' Yn 'ст(x2)' exp-2' Jct(Z) ' dZ]

x i

Поскольку толщина слоя дыма невелика, то x ₁ ния по шлейфу между точками х₂ и х 1

x ₂ , и среднее значение коэффициента рассея-

ст =--In

²⁽ x 2 ^- x 1 )

P ( x 1 )

P (x 2)

В тех ситуациях, когда слой дыма достаточно толст по пространству и плотен и выполняется ^x 2

условие

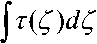
, применим асимптотический алгоритм определения пространственного распре- xi деления а(х):

P (x)' x2 ст( x) = —----------

2 J P ( Z ) • z ² d Z

x

Для интерпретации результатов лазерного зондирования полезным является использование поляризационных эффектов. Из теории рассеяния света следует, что ансамбль частиц, состоящих из идеальных сфер, при рассеянии строго назад должен сохранять состояние поляризации, присущее зондирующему пучку. Например, если лазерное излучение линейно поляризовано в какой-то плоскости, то и однократно рассеянное в направлении 1800 оно поляризовано в этой же плоскости. Поэтому наблюдающаяся в экспериментах деполяризация однократно рассеянного излучения обусловлена отклонением формы частиц от сферической. Так будет при зондировании дымов вблизи.

На более значительных дистанциях на приемник начнет попадать излучение, фотоны которого многократно испытали рассеяние на частицах дыма, капельках и тому подобное. В этом случае величина деполяризации эхосигнала будет возрастать по мере углубления в облака. Для светлого дыма, тумана над градирней деполяризация будет возрастать достаточно быстро. Для темного дыма этот процесс будет происходить медленнее, так как в темном веществе поглощается больше фотонов и снижается кратность излучения, отраженного в приемный телескоп.

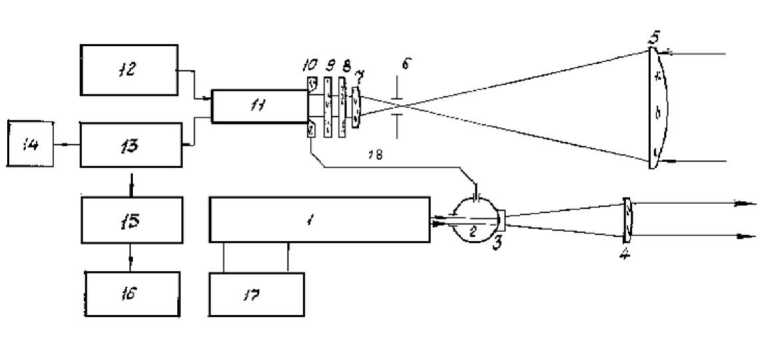
Рис.1. Принципиальная схема лидара

Принципиальная схема лидара приведена на рисунке 1.Здесь 1 – лазерный излучатель типа ИЛТИ – 405, работающий на кристалле иттрий – алюминиевого граната; 2 – фотометрическая сфера для усреднения излучения; линзы 3 и 4 образуют телескоп коллиматора; линзы 5 и 6 – приемный телескоп; 6 – сменная диафрагма; 8 – интерференционный светофильтр; 9 – поворотный поляроидный фильтр; 10 – стеклянное кольцо для подачи излучения от световода 18 на катод фотоумножителя (ФЭУ) 11; 12 – блок высоковольтного питания фотоумножителя; 13 – аналогово-цифровой преобразователь (АЦП) с телевизионным дисплеем 14; 15 – интерфейс связи с ЭВМ 16; 17 – блок обеспечения работы лазера.

Проходящий в атмосфере вдоль оптической оси лазера импульс света частично рассеивается на встречающихся на его пути частицах дыма, капельках воды и иных аэрозолях. Чем выше счетная концентрация аэрозолей и их размер (т. е. их массовая концентрация), тем больше мощность излучения, собираемая приемным телескопом 5–7.

АЦП преобразует непрерывный сигнал с ФЭУ 11, промодулированный атмосферными неоднородностями, в дискретный, цифровой вид, удобный для обработки на ЭВМ.

На телемониторе в реальном масштабе времени и в виде, близком к обычному телевизионному стандарту, представлены 256 эхосигналов лидара. При каждой последующей вспышке лазера один новый эхосигнал появляется на экране, а последний на данный момент исчезает с него. При этом можно вести зондирование дымов над срезами труб ТЭС как по вертикали, так и вдоль горизонтальной трассы в предположении, что атмосфера близка к однородной.

Калибровка лидара ставит в соответствие мощность принятого сигнала Р(x) мощности излученного импульса Р 0 . Последняя составляет миллионы ватт в импульсе и, естественно, не может быть прямо определена фотоприемником. Наиболее приемлема калибровка по свободной атмосфере, когда оценивается оператором лидара метеорологическая дальность видимости S M . Она связана с коэффициентом рас- 3.9

сеяния соотношением σ =           , когда

SM

σ ( x ) =

P ( x ) ⋅ x ² χ ⋅ T 0 ² - 2 ^x ∫ ² P ( ζ ) ⋅ ζ ² d ζ

Здесь x – расстояние, от которого начинается регистрация принимаемого сигнала; T ₀ ² = exp[ - 2 σ x ] – пропускание атмосферы до этой дистанции; χ – калибровочная постоянная, мультипликативно объединяющая все входящие в (1) константы, включая индикатрису атмосферы γ π . Если проводить зондирование по горизонтали в условиях, когда можно положить σ(x)=const, записать решение (8) для двух расстояний x 1 и x 2 и приравнять их друг к другу, то получим

2 χ = ₂

T ₀

⋅

F ( x 1 ) x 1^{2 x} ∫ ² F ( ζ ) ζ ² d ζ x ₁

F ( x ₁) x ₁ ² - F ( x ₂) x ₂ ²

При выполнении такого рода калибровки по результатам зондирования атмосферы с крыши административного здания Улан-Удэнской ТЭЦ-1 в восточном направлении было получено, что χ =2,1∙10⁹. Это значит, что величина 0,5∙Р 0 ∙с∙τ∙S 0 ∙η∙γ π =2.1∙10⁹ единиц кода аналогово-цифрового преобразователя

(АЦП) (в среднем). Мощность лазера эквивалентна 7,47∙1010 единиц кода АЦП.

В качестве эксперимента было проведено зондирование труб Улан-Удэнской ТЭЦ-1. Расстояние по трассе с наклоном 240 до границы дымового выброса равнялась 630 м. Луч лазера проходил в шлейфе на высоте 20-25 м над устьем трубы, высота которой составляет 180 м. Лидар располагался на высоте около 25 м над уровнем земли.

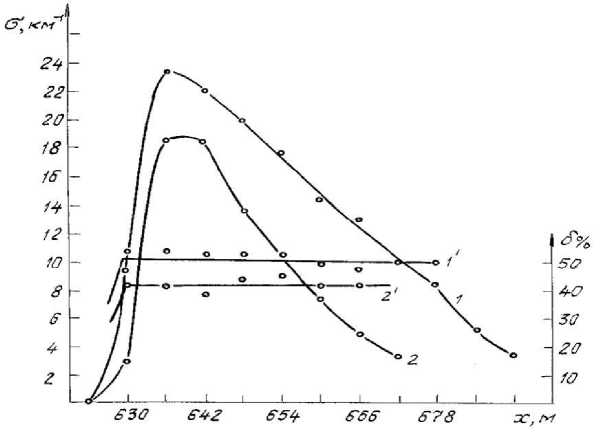
Рис.2. Результаты зондирования шлейфа

На рисунке 2 представлены результаты зондирования шлейфа, который визуально и по видеозаписи стабильно представлял собой довольно прозрачное образование.