Организация обзора пространства в многопозиционной радиолокационной системе с некооперируемым источником подсвета на основе комбинаторного принципа

– при использовании МПРЛС в условиях антагонистического конфликта обеспечение высокого качества канала информационного обмена будет затруднено из-за воздействий противостоящей стороны (уничтожение, повреждение, радиоэлектронное подавление и т.д.);

– при построении МПРЛС с НИП обеспечение качества за счет повышения требований к количественным характеристикам канала информационного обмена повышает уязвимость системы, отказ канала информационного обмена приведет к отказу всей системы.

Таким образом, по мнению авторов, основной принцип организации информационного обмена в МПРЛС с НИП можно сформулировать так: зависимость качества МПРЛС с НИП от количественных характеристик канала информационного обмена должна быть минимальна.

Данный принцип противоречив, решение противоречия может быть одним из подходов к развитию МПРЛС с НИП.

В настоящей работе предметом рассмотрения является возможная реализация обзора пространства МПРЛС с НИП, позволяющая снизить требования к количественным характеристикам канала информационного обмена за счет уменьшения объема передаваемой информации.

В пассивной радиолокации обзор пространства возможно реализовать поисковым и бес-поисковым способами.

При реализации поискового способа (рис. 1) обзор пространства обеспечивается электронным, механическим или комбинированным способом качания луча диаграммы направленности антенной системы (ДНА). При этом возникают ограничения на возможности обзора: необходимо решать задачи выбора периода обзора и синхронизации обзора пространства приемными пунктами, что достаточно трудно реализовать.

Беспоисковый способ пеленгации реализуется применением всенаправленных антенн, антенных устройств с многолучевыми статичными диаграммами направленности (рис. 2).

Рассмотрим МПРЛС, состоящую из трех приемных пунктов (ПП), с многолепестковыми (многолучевыми) ДН антенн в азимутальной плоскости (рис. 2). Каждый ПП МПРЛС, изображенный на рис. 2, имеет ДНА, состоящую из 32 лепестков с шириной каждого лепестка приблизительно 5,6 ° , данные значения выбраны в качестве примера.

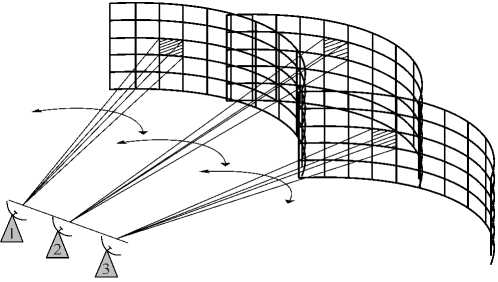
Рис. 1. Поисковый способ обзора пространства МПРЛС

Fig. 1. Search method of the survey space multi-radar system

D2 [км]

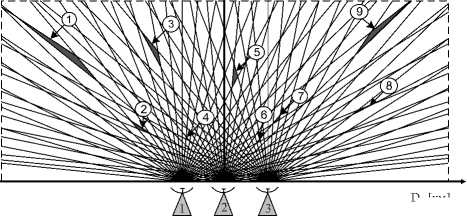
D1 [км]

Рис. 2. Беспоисковый способ обзора МПРЛС с многолучевыми ДНА ПП

Fig. 2. A searchless way to review a multi-position radar system with multipath antenna patterns of receiving points

Если каждому лепестку ДН ПП присвоить номер от 1 до N (где N – число лепестков ДНА) и разместить ПП на некотором удалении друг от друга, то каждой точке оцениваемого пространства можно поставить в соответствие комбинацию чисел – номеров лепестков ДН ПП, то есть сформировать своего рода систему координат.

Например, на рис. 2 представлены 9 закрашенных областей пространства, выбранных случайным образом и обозначенных цифрами. Данные области получаются следующим образом: если многолепестковые ДНА 1-го, 2-го и 3-го ПП принять соответственно за генеральные совокупности множеств статичных секторов обзора ПП (1):

А = { a 1 , a ₂, a₃,..., a n }, n = ( в / в л + 1) - целое ,

B = ^{ b 1 ,b 2 ,a ^3,...^, b n }, n = ^{( в} / ^в л + 1) ^- целое ,                                    (1)

C = {C1, c 2, c 3,..., Cn}, n = (в / вл +1) - целое , где А – множество статичных секторов обзора ПП А; β – сектор обзора ПП; βл – ширина одного лепестка ДНА; n – количество лепестков ДНА ПП; В – множество статичных секторов обзора ПП В; С – множество статичных секторов обзора ПП С, то взаимные пересечения лепестков ДНА ПП образуют области пространства, которые будем называть объемами взаимного разрешения. Множество объемов взаимного разрешения обозначим

X = ⁽ x 1 , X 2 , x 3 ,..., x k ), k ^- целое.                                                      ⁽²⁾

Множество X получается на основе пересечений множеств А, B и С, М - число возможных пересечений ДНА всех ПП (мощность множества X ).

А = A I B I C .. Xi. ak, ak e A, к e {^Д..., N} л л Xi. bs, bs e B, s e W,..., N} л                                             (3)

л x i e c u , c u e C , u e {1,2,3,..., N } .

Выбранные области принадлежат множеству Х.

Если обозначить номера лепестков каждого из трех ПП справа налево (рис. 3), то x_k, k e {1,^,9} (закрашенные области) соответствуют комбинации чисел, представленных в табл.

Таблица

Table

Номер ПП	Номер оцениваемой области
	1	2	3	4	5	6	7	8	9
1	9	10	15	19	22	28	27	28	27
2	8	6	23	9	18	24	23	27	23
3	6	5	9	6	13	14	18	26	23

Таким образом, если в одной из областей пространства, характеризуемой множеством x i , будет воздушный объект, то определение его местоположения возможно по анализу в пункте совместной обработки информации комбинации номеров каналов ПП, в которых осуществлен прием сигнала от воздушного объекта.

За счет передачи между приемными пунктами и пунктом совместной обработки только служебной информации и номеров каналов, в которых получены сигналы, снижаются требования к количественным характеристикам каналов информационного обмена. По комбинации каналов можно отождествить воздушный объект и однозначно определять положение воздушных объектов в пространстве.

Число возможных комбинаций каналов ПП, без учета пространственного расположения, составит:

m = n^Q ,

где Q – число ПП в МПРЛС; n – число лепестков в ДНА каждого ПП (при условии, что ДНА ПП одинаковы).

Для рассматриваемого примера число возможных комбинаций – размещений, исходя из теории комбинаторики формулы (4), составит m = 32768, но такого числа взаимных пересечений лепестков ДНА не будет за счет пространственного разноса ПП и ДНА в пространстве. Например, 1-й лепесток первого ПП не имеет взаимных пересечений с 32-м лепестком третьего ПП.

Проведем оценку комбинаторного подхода в организации обзора пространства в МПРЛС, в качестве количественных показателей выберем:

– число объемов взаимного разрешения, мощность множества: | X | = M ;

– максимальную площадь сечения объемов взаимного разрешения ДНА: max(|xi|), ie{1,2,3,^, M};                                                           mM

Z,=

- среднюю величину площади сечения объемов взаимного разрешения ДНА: ———-

M

В качестве аргументов при оценке указанных выше показателей выберем: ширину одного лепестка ДНА ПП по азимуту ( б ) и удаление одного из ПП от центрального (R₁₃ - для системы из трех и R₁₄ – для системы из четырех ПП).

На рис. 4 приводится результат оценки мощности множества | X | в зависимости от выбранных аргументов: ширина луча диаграммы ДНА: 5 ° , 10 ° , 15 ° , 20 ° , удаление ПП от центрального:

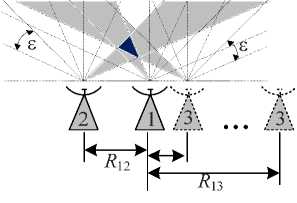
а

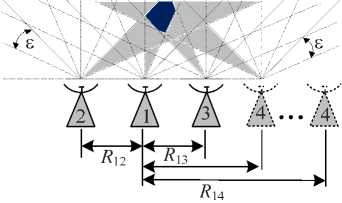
б

Рис. 3. Методика оценки показателей МПРЛС при беспоисковом способе обзора: а – из трех ПП (R13 – аргумент пространственной конфигурации системы); б – из четырех ПП (R14 – аргумент пространственной конфигурации системы)

Fig. 3. Methodology for estimating the performance of a multi-position radar system with a searchless survey method: a – of 3 receiving points (R13 is the argument of spatial configuration of the system); б – of 4 receiving points (R14 is the argument of spatial configuration of the system)

л

^

R 14 = 60 [км]

для 3- х ПП R 13 = 14 .. – 60 км R ₁₂ = –10 км

R 14 = 14 [км]

R 13 = 60 [км]

для 4- х ПП R 14 = 14 .. – 60 км R 12 = –10 км R 13 = 10 км

R 13 = 14 [км]

20 ε [ град .]

Рис. 4. Кривые оценки мощности множества объемов взаимного разрешения от ширины луча ДНА ПП и аргументов пространственной конфигурации МПРЛС (R 13 , R 14 )

Fig. 4. Curves for estimating the power of a set of volumes of mutual resolution of the beam width of the antenna of receiving points and spatial configuration arguments (R13, R14)

– системы из трех ПП (рис. 3 а ) R₁₃=14÷60 км с шагом в 2 км, при R₁₂=10 км;

– системы из четырех ПП (рис. 3 б ) R 14 =14÷60 км с шагом в 2 км, R 12 =10 км, R 13 = –10 км;

– оцениваемая область пространства имеет размеры (рис. 2): D₁= –300÷300 км, D 2 =0÷300 км.

Полученные результаты позволяют сделать следующие выводы:

– зависимость | X |(ε, R 1 x ) носит нелинейный характер;

– для случаев трех и четырех позиций ПП зависимости | X |(ε, R ₁₃) и | X |(ε, R ₁₄) имеют одинаковую закономерность. За счет увеличения числа ПП и уменьшения ширины лепестков ДНА происходит увеличение | X |. При этом большее влияние оказывает ширина лепестка ДНА ( ε );

• -    при значении ширины лепестка ДНА £>15° число ПП, их взаимное расположение не оказывают существенного влияния на | X | и, как следствие, на точность таких систем;

• -    при ширине лепестка ДНА £<10° число ПП, их взаимное положение существенно влияют на | X |;

• -    при малых значениях ширины ДНА за счет оптимального размещения ПП можно добиться увеличения | X |.

Следует отметить, что системой из трех ПП можно добиться такого же показателя | X |, как и для системы из четырех ПП, за счет оптимального размещения ПП.

На рис. 5 представлен результат оценки максимальной площади сечения объема взаимного разрешения max(| x i |(е, R 1 _x )), i e {1,2,3,..., M }, в зависимости от ширины лепестка ДНА в азимутальной плоскости при перемещении одного из ПП относительно центрального при 0 , 300-300 км, D₂ 0-300 км: а) - система из трех ПП, б) - система из четырех ПП. Полученный результат представлен в нормированном, прологарифмированном виде по значению максимальной площади сечения объема взаимного разрешения Хтах при ширине лепестка ДНА ПП £=20°, для удобства визуального представления и оценки малых диапазонов изменения исследуемых зависимостей.

Полученные зависимости на рис. 5 позволяют сделать выводы:

• -    для системы из трех ПП их расположение оказывает влияние на значение max(| x i |(e, R ₁₃)). Явно это проявляется при малых значениях ширины лепестков ДНА: так, при £=5° увеличение наблюдается в диапазоне R ₁₃=25>38 км. При £=10° увеличение начинается с R =45 км . При значениях £=15° и £=20° отмеченного увеличения нет, так как оно не по- i3

падает в оцениваемый диапазон дальностей D 1 и D₂ (рис. 2);

тттт

• –    для системы из трех ПП на всех четырех зависимостях можно отметить оптимальное (наименьшее) расстояние удаления третьего ПП от центрального. Так, при £=5° удале-

  
  

  -2

  -4

  -6

  
  

  -8

  -10

  -12

  -14

  -16

  
  

  10 lg(max ( ^x i (^Е, R 1з )) X тax

  
  
  
  
  
  
  

  НА ПП . плоск.

  
  

  0 [км]

  
  

  ¹⁸ 10   15   20   25   30   35   40   45   50   55   60 R 13

  
  

  [км]

  
  

  а)

  
  
  

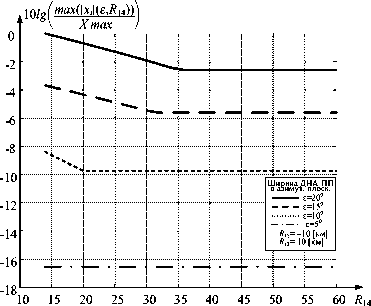
  [км]

  б)

  
  

Рис. 5. Оценка максимальной площади сечения объемов взаимного разрешения МПРЛС для оцениваемого пространства D=600*300 км: а – МПРЛС из трех ПП; б – МПРЛС из четырех ПП

Fig. 5. Estimation of the maximum cross-sectional area of volumes of mutual resolution of a multi-position radar system for the estimated space D = 600*300 km: a – from 3 receiving points; б – from 4 receiving points ние составляет R13=10 км, при 8=10° R13 =20 км, при 8=15°R13 =33 км, при 8=20° R13 =35 км. Можно утверждать, что с дальнейшим увеличением ширины лепестков ДНА приращения уменьшаются;

• -    для системы из четырех ПП зависимость max(| x i |(е, R ₁₄)) уменьшается. При малой ширине лепестков ДНА (8=5°) зависимость в оцениваемом диапазоне дальностей отсутствует. При больших значениях ширины лепестков ДНА (8=10°' 20°) можно отметить оптимальные, минимальные удаления, причем они совпадают с показателями, указанными выше для системы из трех ПП.

Однако полученные результаты были рассчитаны для оцениваемого пространства размерами 600 км на 300 км. Если провести оценку МПРЛС по тому же критерию, но для меньшего оцениваемого пространства, то получится результат, представленный на рис. 6, 7. На рис. 6 изображен результат оценки max(| x i |(е, R 1 x )), i е {1,2,3,..., M } при размерах оцениваемого пространства D ,   150-150 км, D₂ 0-300 км.

На рис. 7 видим результат оценки max(| x i |(e, R ₁₃)), i е {1,2,3,..., M } МПРЛС из трех ПП при размерах оцениваемого пространства D 1 = -75-75 км, D₂=0-150 км.

Полученные зависимости указывают на то, что при оценке необходимо вводить еще один аргумент: D = [ D 1 , D ₂], но оптимальное удаление ПП друг от друга выбирать по правилу

R хопт . = min(max(*, R х ))), при R i_х ^ 0.                         (5)

На рис. 8 представлен результат оценки зависимости средней площади сечения объемов взаимного разрешения МПРЛС из трех и четырех ПП от ширины лепестка ДНА в азимутальной плоскости при перемещении одного из ПП относительно центрального, при D 1 = -300-300 км, D 2 =0-300 км.

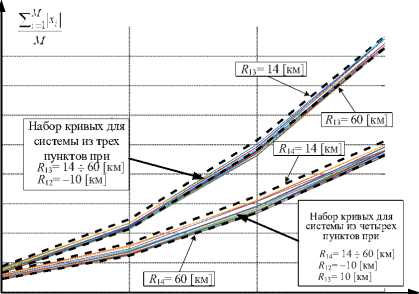
На рис. 9 изображен результат оценки зависимости средней площади сечения объемов взаимного разрешения МПРЛС из трех ПП от ширины лепестка ДНА в азимутальной плоскости

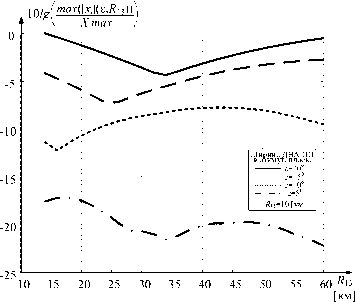
а)

Рис. 6. Оценка максимальной площади сечения объемов взаимного разрешения МПРЛС для оцениваемого пространства D=300*300 км: а – МПРЛС из трех ПП; б – МПРЛС из четырех ПП

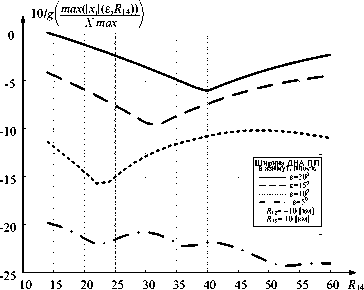
[км]

б)

Fig. 6. Estimation of the maximum cross-sectional area of volumes of mutual resolution of a multi-position radar system for the estimated space D = 300*300 km: a – from 3 receiving points; б – from 4 receiving points

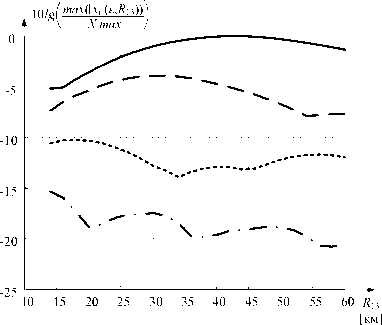
Рис. 7. Оценка максимальной площади сечения объемов взаимного разрешения МПРЛС из трех ПП для оцениваемого пространства D=150*150 км

Fig. 7. Estimation of the maximum cross-sectional area of volumes of mutual resolution of a multi-position radar system of 3 receiving points for the estimated space D = 150*150 km

20 ^£

[град.]

Рис. 8. Кривые средней площади сечения объемов взаимного разрешения МПРЛС

Fig. 8. Curves of the average cross-sectional area volumes of the mutual resolution of the multi-position radar system при перемещении одного из ПП относительно центрального: а) D1= –300÷300 км, D2=0÷300 км;

• б) D1= –150÷150 км, D2=0÷300 км; в) D1= –75÷75 км, D2=0÷150 км.

Анализ полученных результатов показывает:

• -    изменение аргумента R 1 x влияет незначительно на среднюю площадь сечения объема взаимного разрешения. По диапазону семейства кривых можно утверждать, что данная зависимость увеличивается при увеличении числа ПП (семейство кривых для четырех ПП шире, чем семейство кривых для трех ПП);

• -    изменение аргумента £ оказывает большее влияние на оцениваемую величину относительно R 1 x . Величина средней площади сечения объемов взаимного разрешения изменяется в 10 раз при £=20° относительно величины при £=5° ;

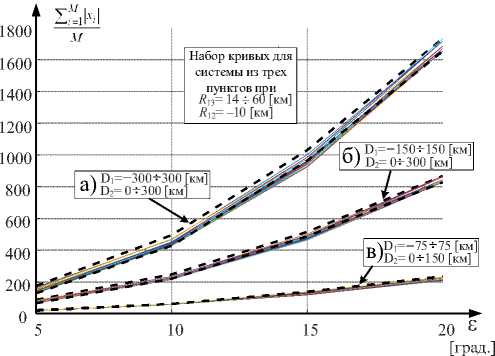
Рис. 9. Кривые средней площади сечения объемов взаимного разрешения МПРЛС

Fig. 9. Curves of the average cross-sectional area of volumes of mutual resolution of a multi-position radar system

• –    закон изменения средней площади сечений объемов взаимного разрешения для систем из трех и четырех ПП имеет нелинейный характер. Если данную зависимость аппроксимировать параболой

_∑ M _{x i}

—i r! ( е ) = а е ,                                                                    (6)

M то относительно результатов на рис. 9 а3ПП = 4,5, а4ПП = 2,6, а отношение a3ПП = 1,7. Данная a4ПП пропорция показывает выигрыш системы из четырех ПП относительно системы из трех ПП. Пропорция подтверждается и результатами, полученными при ограничении оцениваемого пространства для значений:

_D1=         км, D        км; D i =       км, D ⁵ км.

Таким образом, приведенные выше оценки могут дать минимальные характеристики по точности для решения радиолокационных задач. Если необходимо измерить три координаты в, e, r воздушного объекта (ВО), то, используя показатели, можно выработать правило:

^тах( А У , ^^в, A г) = s ^up( X ⁽ Л 1 x , ^е, D)), X = { x ^{1 ,} x 2 , x ₃,...,| X },                 (7)

где ∆ θ – неопределенность в измерении азимута ВО; ∆ β – неопределенность в определении угла места ВО; ∆ r – неопределенность в определении дальности ВО.

Исходя из сформулированного правила, можно сделать вывод: ширина луча ДНА должна стремиться к минимуму, оцениваемая область пространства (D[D 1 ,D₂]) - задаваемая величина (const), R 1 x - регулятор пространственной конфигурации МПРЛС - оптимально настраиваемая величина.