Организация передачи данных по гидроакустическому каналу в подземных водопроводных сетях

Трубы подземных водопроводных сетей подвержены нагрузкам, вызванных комбинацией действующих внешних и внутренних сил. Внутренние силы обусловлены действием давления воды, а внешние силы непосредственно воздействием грунта. Подземные труба подвержена действию радиальных нагрузок сжатия и круговых нагрузок сдвига, также вызываемых окружающим грунтом. Радиальные нагрузки вызывают деформацию трубы и кратковременное уменьшение диаметра. Обычно радиальные нагрузки не однородны и за счет этого подземная труба подвержена кольцевому прогибу. Если труба закопана в слабом, вязком грунте с небольшой жесткостью по сравнению с жесткостью трубы, то кольцевой прогиб зависит непосредственно от характеристик трубы. Если труба проложена в уплотненном (гранулированном) грунте, то кольцевой (боковой) прогиб будет зависеть от взаимодействия трубы и грунта [1 – 3].

Для труб в подземных водопроводных сетях внешние силы – это нагрузка грунта и временные нагрузки. Внутреннее давление может увеличивать или уменьшать напряжения или деформации, возникшие за счет действия внешних сил (рисунок 1).

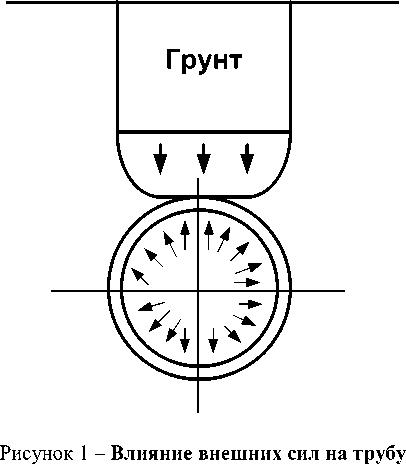
Когда труба закопана в слабом, вязком грунте с маленькой жесткостью или без нее по сравнению с жесткостью трубы, кольцевой прогиб в основном зависит от характеристик трубы. С другой стороны, при уплотненном, гранулированном грунте засыпки, боковой прогиб зависит от взаимодействия трубы и окружающего грунта. Жесткость грунта обычно характеризуется коэффициентом пассивного сопротивления, мерой совместной жесткости грунта и трубы. Радиальная нагрузка сжатия и кольцевой прогиб или изгибание, которые имеют место у гибких труб, вызывают деформацию и напряжение стенок трубы. Если труба помещена в плотный грунт, она подвержена действию радиального давления грунта, на стенках трубы возникает круговое напряжение сжатия. Обычно радиальное давление грунта, вызывающее напряжение не является однородным.

В работе проведем оценку гидроакустического канала связи в подземных водопроводных сетях, при этом предположим, что радиальное давление грунта однородно и равно вер- тикальному давлению грунта на верхнюю точку трубы.

Результаты расчетов

Рассмотрим случай, когда труба не является упругой с внутренним радиусом r и внешним радиусом r 2 , тогда акустическая волна излучается в грунт и в стенки трубы (рисунок 2). Часть переданного сигнала будет распространяться в водном потоке, а также через стенку трубы и грунт. В городских условиях скорость волн сдвига меняется в интервале от 30 до 300м/с, редко (для линий глубокого заложения до 450м/с) [1 - 3]. Скорость распространения продольных волн в грунте меняется в пределах от 600 до 1000м/с (для твердых грунтов до 1500м/с). Водонасыщенность грунта приводит к росту скорости продольных волн и практически не изменяет скорости поперечных волн. Плотность грунта меняется слабо от 1600 до 1900кг/м³ и не является определяющей характеристикой при расчетах.

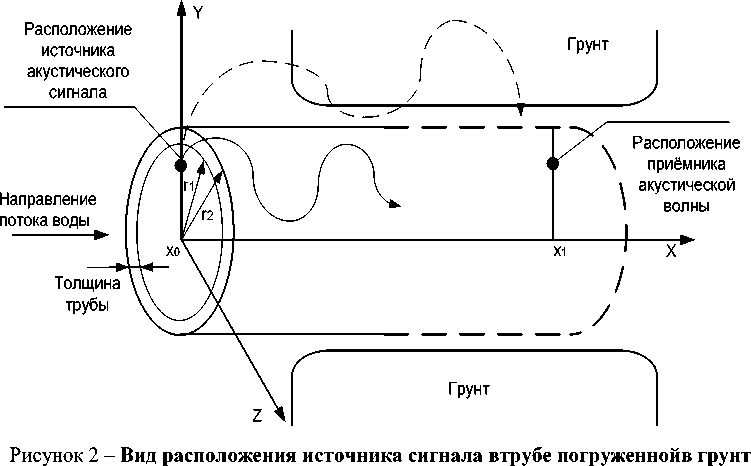
Рассмотримпередаточнуюфункцию, связывающую параметры акустического давления в радиальном направлении p_r и радиальной скорости v_r во внутренних и внешних гра-

ницах	трубы	(	r = r	и	r =	r 2 )
"P r 2 "	L i L 2	"pr "			p
=			,    где	L 1	____        ' 2
L v J	_ L з L 4 _	L V r i _			P r i	vr 1 = 0
p		v		v
L 2 =	, L 3	=	, L 4	= ^2.	•
v r	P r = 0	P r i	v r = 0	v r i	P r = 0

Запишем выражения для акустического давления в радиальном направлении и радиальную волновую скорость в виде [4 - 5]:

P_r( п, ю, r ) = - i юр [ aH ° (n r ) + bH 2 (n r )];

vr(П,Юr) = — [aHо (Пr) + bHо2 (Пr)] , юр где: H1(nr) - функция Ханкеля первого рода, для волн, распространяющихся в направлении грунта; H2(nr) - функция Ханкеля второго рода, для отраженных волн, распространяю- щихся во внутреннюю область трубы; a, b константы.

Тогда в матричной форме

–

P 1 . v r

I a =4 „

;

Pr. . k

г , 1 a r2 lb ’

где:

— i юр H 0 ( n , 1 )

¹ M ^] = i ¹ H 11 ( n , 1 ) L^юр

— i юр H 02 ( n , 1 )

— H ²(n , 1 ) юр

• ••

• ••

11    *П

—

1    r14 _ i юр H0(n ,2)

[ M > 2T H J ( n r , )

Ltop

— i юр H 0 ( n , 2 )

— H ²(n , 2 ) юр

•••

•••

21 ^r 22

•

^r 24 _

Значения констант

a

b

pr

v

pr

v

•

Умножаем части полученного выражения матрицу[m,2 ] и Ml:

на

p

v

v

p

v

pr

v

;

•

Произведение [ M ] [ m, ]^{— 1}

- матрица

передачи от внутренней области во внешнюю

область и соответственно [ M ' ] [ M ₂ ]^{— 1}

–

мат-

рица передачи от внешней области во внутреннюю область.

Проведем замены в матрицах:

21 ^r 14

—

23 r 14

—

^Г22 ^Г13 )   ^{( Г}21^Г12 + ^Г22 ^, 11⁾

^Г24 ^Г 1з )   ^{( —} r 23 r 12 + r 24 ^Г 11 )

A ,

,

где

[ M ,._r2] - матрица передачи в направлении от радиуса , до ^r 2 ; ^A , = ^r n^4 ^— r _i2 ^r ,3•

Тогда коэффициенты матрицы

^L 1 ^L - 2

^L 3 L 4

^L1 = ^— i П n ^r 1 [ ^{H 1 (} n ^r 2 ) ^H 1² ( n r ) ^— H 0² ( n ^r 2 ) H ¹ ( n ^r 1 ) ] ;

L 2 = П n , 1 рю[ H 0 ( n , 2 ) H 0² ( n , 1 ) — H 0² ( n , 2 ) H ¹ ( n , 1 ) ] ;

L 3 = ⁿ ^ [ H ^{1 (} n ^r 2 ) H ^{2 (} n r ) ^— H 1 ^{2 (} n ^r 2 ) H ^{1 (} n ^r 1 ) ] ;

4 рю

^L 4 = ^— i П n ^r 1 ^{[ H} 1^{2 (} n ^r 2 ) ^H 0 ⁽ n ^r 1 ) ^{— H 1 (} n ^r 2 ) ^H 0^{2 (} n ^r 1 ) ] •

Полученные расчетным путём коэффициенты L — L ₄, и далее через матрицу передачи, позволяют определить величину акустического давления в радиальном направлении через область стенок трубы и грунта в направлении приёмника акустической волны.

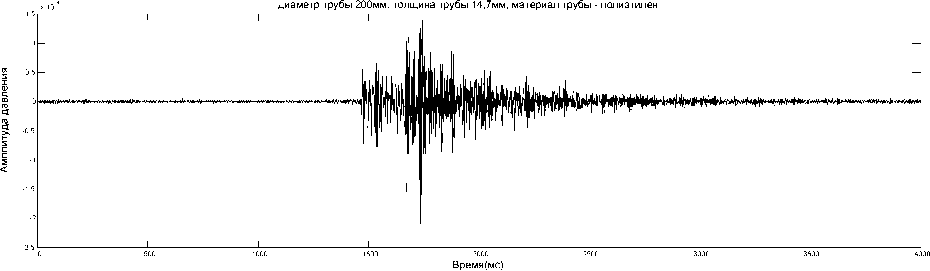
Проведем расчет акустического давления, распространяемого внутри водопроводной напорной трубы из полиэтилена (ГОСТ 185992001, ТУ 2248-016-40270293-2002, рабочее давление 1,0МПа, диаметр 200мм, толщина 14,7мм), и стальной водопроводной трубы бесшовной горячедеформированной (ГОСТ Р53383-2002, диаметр 199мм, толщина 2,0мм). Частота исходного импульса 55кГц; расстояние до приёмника акустического сигнала 400м; плотность стали от 7700 до 7900кг/м3; скорость звука в стальной трубе 5740м/с; плотность полиэтилена от 950 до 960кг/м3; скорость продольных волн звука в полиэтиленовой трубе 2000м/с; постоянная затухания для продольных волн в полиэтилене 0,23непер/см [6÷8]. Временные области распространения акустического давления, приведены на рисунках (3÷5).

Акустическая скорость распространения волны зависит от сопротивлений материалов (вода, полиэтилен, сталь, грунт и т.д.), которые распределяют энергию волны.

На рисунке 3, приведены формы импульсов, прошедшие в грунт через различные материалы труб. Импульс, прошедший в грунт через трубу из полиэтилена ослаблен на 28,5дБ по сравнению с импульсом прошедшим в грунт через стальную трубу. По форме импульса видно, что в грунте не распространяется плоская волна, поэтому можно предположить, что данный импульс в виде шума будет накладываться на плоскую волну, распространяемую внутри трубы.

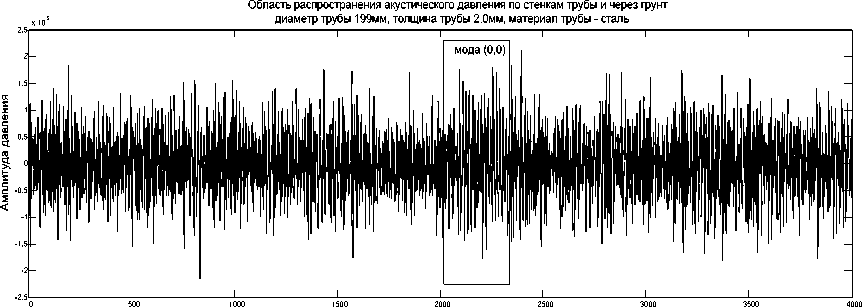
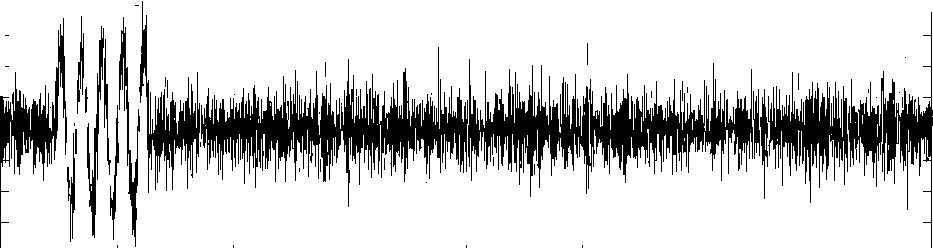
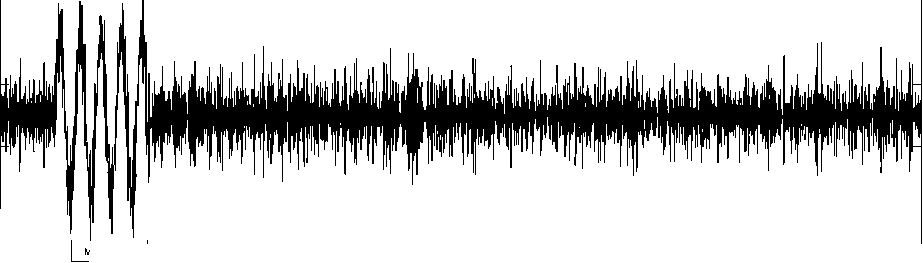
На рисунках 4и 5 видно, что на вход приёмника поступают более быстрые моды, чем плоская волна, прибывшие по стенкам стальной трубы. Наблюдаются и другие моды, распространяющиеся через более длинные пути передачи, включая возможные отражения от стенок стальной трубы и прошедшие через грунт различной плотности. При уменьшении частоты исходного импульса до 5кГц не изменяя диаметр трубы, наблюдаем затухания отраженных сигналов, прошедших через стенки стальной трубы и области грунта на 14дБ (рисунок 5). Импульс с частотой 55кГц возбуждает

Определение диагностических параметров технического состояния дросселей … большее количество мод, что приводит к серь-  этом, высокочастотные режимы затухают бы-

ёзной реверберации сигнала (рисунок 4), при  стрее, чем низкочастотные.

Область распространения акустического давления через трубу в грунт

Область распространения акустического давления через трубу в грунт

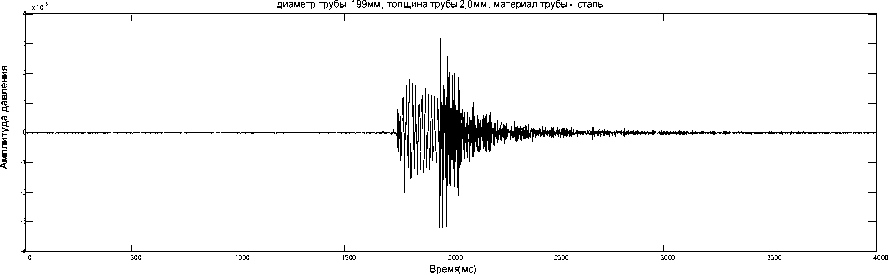
Рисунок 3 – Области распространения акустического давления

Область распространения акустического давления по стенкам трубы

x 10

1.5

диаметр трубы 199мм, толщина трубы 2,0мм, материал трубы - сталь мода (0,0)

0.5

-0.5

-1

-1.5

Время(мс)

Время(мс)

Рисунок 4 – Области распространения акустического давления

-8 0

мода (0,0)

Область распространения акустического давления по стенкам трубы и через грунт частота сигнала 5кГц, диаметр трубы 199мм, толщина трубы 2,0мм, материал трубы - сталь x 104

-2

-4

-6

Время(мс)

Область распространения акустического давления по стенкам трубы частота сигнала 5кГц, диаметр трубы 199мм, толщина трубы 2,0мм, материал трубы - сталь x 104

-2

-4

-6

-8

мода (0,0)

Время(мс)

Рисунок 5 – Области распространения акустического давления

-10

Выводы

• 1.    Отражения акустической волны на границе раздела нескольких сред (вода – стенки трубы – грунт),имеющих разную плотность, будет уменьшать энергию распространяемого акустического давления внутри трубы и увеличивать многолучевое распространение волн.

• 2.    В подземной водопроводной трубе основной волной будет являться плоская волна.

• 3.    Большая часть энергии передаваемого импульса приходится на волны, распространяющиеся через более длинные пути передачи, включая возможные отражения от стенок стальной трубы и прошедшие через грунт различной плотности.