Организация полностью самопроверяемой схемы встроенного контроля на основе метода логического дополнения до равновесного кода "2 из 4"
Автор: Ефанов Д.В., Сапожников В.В., Сапожников вЛ.В., Пивоваров Д.В.
Журнал: Труды Института системного программирования РАН @trudy-isp-ran
Статья в выпуске: 2 т.30, 2018 года.
Бесплатный доступ
Рассматривается задача синтеза самопроверяемой схемы встроенного контроля с оптимизацией структурной избыточности на основе использования метода логического дополнения до равновновесного кода «2 из 4». Разработан способ доопределения значений контрольных функций, позволяющий пошагово устанавливать их вид и при этом обеспечивать решение задачи тестирования соответствующих элементов сложения по модулю два и схемы тестера. При этом в значения функций вводятся неопределенности, что позволяет минимизировать сами функции, и соответственно, упрощать схему блока контрольной логики.
Схема встроенного контроля, логическое дополнение, равновесный код, код
Короткий адрес: https://sciup.org/14916576
IDR: 14916576 | DOI: 10.15514/ISPRAS-2018-30(2)-6
Текст научной статьи Организация полностью самопроверяемой схемы встроенного контроля на основе метода логического дополнения до равновесного кода "2 из 4"
При построении отказоустойчивых компонентов систем автоматического управления широко применяют самопроверяемые схемы встроенного контроля, организуя для объекта диагностирования систему функционального контроля [1-3]. В такой системе реализуется стратегия рабочего диагностирования, когда входные рабочие воздействия на объект диагностирования одновременно являются и тестовыми, а отключение его от работы не является необходимым [4].
Системы функционального контроля в реальных приложениях должны обеспечивать 100%-ное обнаружения ошибок из заданного класса. Причем схема встроенного контроля в составе системы функционального контроля должна быть полностью само проверяемой: любая неисправность из заданного класса должна обнаруживаться в момент первого ее проявления на контрольных выходах в виде формирования защитной комбинации [5, 6].
При синтезе систем функционального контроля используются равномерные блочные коды с избыточностью, не превышающей количества рабочих выходов объекта диагностирования. К таким кодам относятся различные коды с суммированием (коды Бергера [7] и их модификации) и равновесные коды [8]. В процессе синтеза системы функционального контроля используют особенности обнаружения ошибок выбранным равномерным кодом. Например, классические коды Бергера и равновесные коды обладают свойством обнаружения любых монотонных и асимметричных ошибок.
Это свойство позволяет использовать данные коды в процессе построения системы функционального контроля следующим образом [9]:
1) осуществлять поиск групп монотонно (или и монотонно, и асимметрично) независимых выходов объекта диагностирования с последующим их контролем на основе соответствующего кода и объединением контрольных выходов получаемых подсхем контроля на входах самопроверяемой схемы сжатия парафазных сигналов;
2) преобразовывать структурную схему объекта диагностирования в схему с единой группой монотонно (или и монотонно, и асимметрично) независимых выходов с последующим контролем их на основе соответствующего кода.
2. Контроль логических устройств на основе 2/4-кода
Такой способ, как показано в современной мировой литературе по синтезу контролепригодных компонентов систем управления [10-13], применяется довольно часто.
В системе функционального контроля объект диагностирования Fix) снабжается самопроверяемой схемой встроенного контроля в составе блока контрольной логики G(x) и полностью самопроверяемого тестера TSC [14]. Схема блока контрольной логики строится таким образом, чтобы на выходах обоих блоков F(x) и G(x) в процессе нормальной эксплуатации формировались только кодовые слова заранее выбранного блочного кода. Тестер контролирует принадлежность поступающего на его входы кодового слова выбранному коду, и при его нарушении формирует сигнал ошибки [15].
В [16, 17] описана структурная схема системы функционального контроля, включающая еще один блок, помимо обозначенных выше, - блок логического дополнения, образованный каскадом сумматоров по модулю два (XORs). Структура системы функционального контроля, полученная на основе метода логического дополнения, является более «гибкой», чем классическая структура [14], с точки зрения обеспечения самопровсряемости схемы контроля и структурной избыточности получаемого дискретного устройства.
В [23] отмечены существенные преимущества использования 2/4-кода при организации контроля логических устройств автоматики и вычислительной техники по сравнению с другими равновесными кодами. Прежде всего, они заключаются в следующем:
-
1) тестер 2/4-кода (2J4-TSC) имеет простую структуру (рис. 1) и требует для полной проверки всего четырех комбинаций: {ООП; 1100; 1001; 0110} [24];
-
2) Для преобразования любого четырехбитного вектора, формируемого на выходах блока Ffx\ в кодовое слово 2/4-кода потребуется изменение максимум двух функций, а значит, блок логического дополнения будет иметь наименьшую сложность, а блок контрольной логики - всего два выхода [25];
-
3) эксперименты [26, 27] показывают, что использование 2/4-кода для контроля многовыходных логических устройств дает меньшую по сложности схему контроля, чем любых других равновесных кодов.
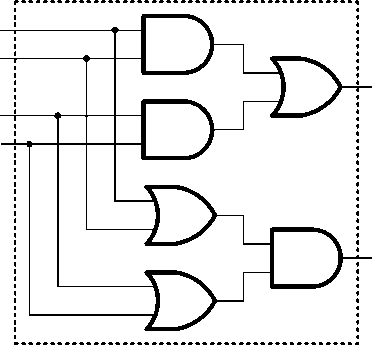
Рис. 1. Наиболее простая структурная схема 2/4-TSC Fig. 1. The simplest structural circuit of 2/4-TSC
Структурная схема системы функционального контроля на основе метода логического дополнения до равновесного 2/4-кода изображена на рис. 2. Эта структура является базовой и используется при контроле группы из четырех выходов. Информационный вектор <Д /з^ /і> преобразуется в кодовое слово 2/4-кода <һд һз hi h\> следующим образом: h\ =fy hi =fi, h3 =f3 ф g3, һд =/д ф g4. Таким образом, в блоке логического дополнения преобразуются только две
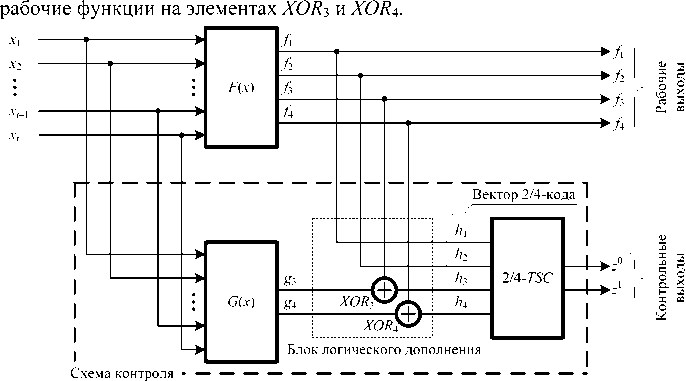
Рис. 2. Структурная схема системы контроля комбинационного логического устройства на основе 2/4-кода
Fig. 2. The structural scheme of the control system of the combination logic device based on 2/4-code
Для обеспечения полной самопровсрясмости системы функционального контроля необходимо обеспечивать формирование хотя бы по разу всех кодовых слов 2/4-кода, а также формирование хотя бы по разу всех тестовых комбинаций каждого элемента XOR - комбинаций {00; 01; 10; 11} [28]. Кроме того, блоки F(x) и G(x) должны быть проверяемыми, то есть любая неисправность из заданного класса должна проявляться на выходах в виде искажений значений. Далее приводится способ построения системы функционального контроля, учитывающий обозначенные выше особенности тестирования ее компонентов.
3. Способ построения ССВК на основе 2/4-кода
Рассмотрим следующий подход к построению самопроверяемой схемы контроля на основе 2/4-кода, ориентированный на доопределении значений двух контрольных функций пошагово, исходя из обеспечения условий тестируемости элементов XOR блока логического дополнения и 2/4- TSC.
Будем рассматривать способ на примере организации схемы контроля для комбинационного логического устройства, заданного в виде таблицы истинности (табл. 1). Устройство имеет четыре входа x1, x2, x3 и x4 и четыре выхода f1, f2, f3 и f4.
Шаг 1. На начальном этапе выбираются две рабочие функции, которые не будут дополняться и будут напрямую соединены с входами тестера. Эти функции выбираются из соображений обеспечения формирования тестового множества для 2/4- TSC {0011; 1100; 1001; 0110}, а именно: хотя бы на одном входном наборе должны быть сформированы хотя бы по разу информационные векторы < f 1 f 2 f 3 f 4 > = < 0 0 ~ ~>, < 0 1 ~ ~>, < 1 0 ~ ~>, < 1 1 ~ ~>. В противном случае окажется невозможным формирование всех тестовых комбинаций для 2/4- TSC . В рассматриваемом примере в качестве не дополняемых функций могут быть выбраны функции f 1 и f 2 . Таким образом, h 1 = f 1 и h 2 = f 2 .
|
Шаг 2. Определяются условия |
дополнения |
функции f 3 , которые должны |
|
учитывать и предыдущий шаг алгоритма. выбираться исходя из выражения J°, если h 3 = к если _~, если Шаг 3. Из предыдущего шага следует, что: f f3, если |
Значение функции h 3 должно h1 h 2 = 1; h1 v h2 = 0; h1 ® h 2 = 1. h 3 = 0; |
|
|
g 3=i f •• , |
если если |
h 3 = 1; h 3 = ~ . |
Выполнение третьего шага для рассматриваемого примера представлено в табл. 1.
Табл. 1. Первый этап получения значений контрольных функций
Table 1. The first stage of obtaining the values of check functions
|
No. |
x 1 |
x 2 |
x 3 |
x 4 |
f 1 |
f 2 |
f 3 |
f 4 |
h 1 |
h 2 |
h 3 |
h 4 |
g 3 |
g 4 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
~ |
~ |
||
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
||
|
2 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
~ |
~ |
||
|
3 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
~ |
~ |
||
|
4 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
||
|
5 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
||
|
6 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
~ |
~ |
||
|
7 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
||
|
8 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
~ |
~ |
||
|
9 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
|
10 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
||
|
11 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
~ |
~ |
||
|
12 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
~ |
~ |
||
|
13 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
||
|
14 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
||
|
15 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
Шаг 4. Частично определенная функция g 3 минимизируется, например, по методу Карно (рис. 3). Миним изиро ванная функция g 3 имеет вид:
g 3 = x 1 x 2 V x 2 x 3 V x 2 x 3 x 4.
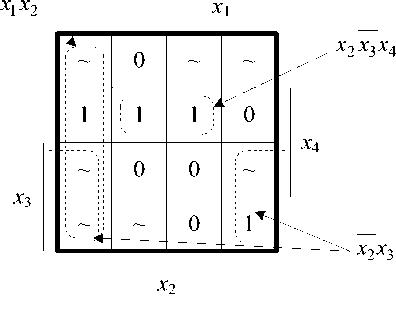
Рис. 3. Минимизация частично определенной функции g 3
Fig. 3. The minimization of a partially defined function g 3
Шаг 5. Вычисляется функция h 3 = f 3 ⊕ g 3 . Результат занесен в таблицу 2.
Табл. 2. Второй этап получения значений контрольных функций
Table 2. The second stage of obtaining the values of check functions
|
No. |
x 1 |
x 2 |
x 3 |
x 4 |
f 1 |
f 2 |
f 3 |
f 4 |
h 1 |
h 2 |
h 3 |
h 4 |
g 3 |
g 4 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
|
2 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
|
3 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
4 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
|
5 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
6 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
7 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
|
8 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
|
9 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
||||
|
10 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
||||
|
11 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
||||
|
12 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
||||
|
13 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
||||
|
14 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
||||
|
15 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
Шаг 6. Необходимо проверить, все ли тестовые комбинации для XOR3 сформированы после выполнения процедуры однозначного определения функции g3. Для этого следует вычислить четыре проверяющие функции, устанавливающие наличие или отсутствие входных наборов, на которых формируются тестовые комбинации элемента сложения по модулю два:
3 г рх = /3g3 = Х[Х2Х3Х4 V XjX2X3X4 V Х[Х2Х3Х4 V
V Х[ Х2Х3 х4 V Х[ Х2Х3Х4 V Х[Х2 х3х4
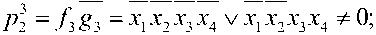
Рз = /з^з =
V Х[Х2 х3 х4 V Х[Х2Х3 х4 V Х[Х2Х3Х4
*0.
Так как все четыре функции не равны 0, то элемент XOR3 тестируется.
Если же проверка показала отсутствие какой-либо тестовой комбинации для элемента XOR3, то выполняется коррекция функции g3.
Шаг 7. Коррекция функции g3 требует доопределения данной функции на неопределенных значениях в соответствии с требуемой тестовой комбинацией. Для этого по формуле g, = hx © /z 2 находятся те входные наборы, на которых функция g3=~. Далее осуществляется доопределение функции g3 на установленных входных наборах для обеспечения формирования соответствующей тестовой комбинации элемента XOR3.
В случае если процедура коррекции значения функции g3 не дает возможности формирования всех проверяющих комбинаций, осуществляется замена функции g3 на gA. Действия шагов 2-7 повторяются. В случае, если результат также не достигнут, в качестве не дополняемых функций выбирают другие функции и процедура повторяется.
Шаг 8. Определяются значения функции g^:
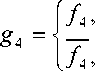
если hxh2 v hxh3 v h2h3 = 1;
если hxh2 v hxh3 v h2h3 * 1.
Условия выбора значений функции g4 определяются исходя из проверки наличия в уже определенных значениях разрядов кодового слова < Ai Аг Аз ~ > наличия двух единичных значений. Так как функция g3 однозначно определена, функция g4 также определяется однозначно (см. табл. 2).
Шаг 9. Выполняется процедура проверки формирования полного множества тестовых комбинаций для элемента XOR^.
Px=hg^ = ххх2х3х4 0;
4 г
Pi = Л
g4 = хх х2х3 х4 V хх х2 х3 х4 V
v хх х2 х3х4 v хх х2х3х4 v ххх2 х3 х4 0;
Рз = Рд§4 = ххх2х3х4 v ххх2х3х4 v ххх2х3х4 Ф 0.
V хх Х2Х3 х4 V ХхХ2 Х3Х4 V ХхХ2Х3Х4
Поскольку все проверяющие функции не равны нулю, элемент XOR4 полностью тестируется.
Шаг 10. Проверяется наличие среди кодовых слов < h\ Аг Аз ^4> всех тестовых комбинаций 2/4-TSC. В рассматриваемом случае они формируются.
Таким образом, представленная последовательность действий по доопределению значений контрольных функций, позволяет однозначно установить значения контрольных функций на всех входных наборах, а значит, полностью позволяет синтезировать схему контроля.
6. Заключение
Представленный способ построения схемы встроенного контроля для комбинационных логических устройств позволяет достичь свойства ее самопроверяемости за счет последовательного доопределения значений контрольных функций.
Недостатком способа следует признать большое количество операций по доопределению и ограниченность реальным числом входных переменных (не более 30 - 35 - это пределы мощности современных вычислительных систем). При большом количестве входных переменных (более 35) следует применять декомпозицию устройства и выделение отдельных подсхем в его составе. Еще одним недостатком является то, что способ ограничен для его использования при построении схем контроля для логических устройств с малых числом входов (например, при 3 входах), так как имеется малое число вариантов дополнений.
Способ построения схемы контроля по методу логического дополнения для 2/4-кода универсален, и с учетом того факта, что 2/4-7SC имеет простую структуру, позволяет синтезировать схемы встроенного контроля со структурной избыточностью, не превышающей избыточность схемы контроля при использовании метода дублирования. Такое заключение может быть сделано на основании большого количества экспериментов по применению равновесных кодов при организации самопроверяемых схем контроля, в том числе, опубликованных в известных источниках [26].
Список литературы Организация полностью самопроверяемой схемы встроенного контроля на основе метода логического дополнения до равновесного кода "2 из 4"
- Kubalík P., Kubátová H. Parity Codes Used for On-Line Testing in FPGA. Acta Polytechnika, 2005, Vol. 45, No. 6, pp. 53-59.
- Ubar R., Raik J., Vierhaus H.-T. Design and Test Technology for Dependable Systems-on-Chip (Premier Reference Source). -Information Science Reference, Hershey -New York, IGI Global, 2011, 578 p.
- Borecký J., Kohlík M., Kubátová H. Parity Driven Reconfigurable Duplex System. Microprocessors and Microsystems, 2017, Vol. 52, pp. 251-260, DOI: 10.1016/j.micpro.2017.06.015
- Objects and Methods of On-Line Testing for Safe Instrumentation and Control Systems/A.V. Drozd, V.S. Kharchenko, S.G. Antoshchuk, Ju.V. Drozd, M.A. Drozd, Yu.Yu. Sulima. Kharkov, National Aerospace University "KhAI", 2012, 614 p..
- Parkhomenko P.P., Sogomonyan E.S. Technical Diagnosis Fundamentals (Diagnostic Algorithm Optimization, Apparatus Means). Moscow: Energoatomizdat, 1981, 320 p..
- Sogomonyan, E.S., Slabakov E.V. Self-Checking Devices and Fault-Tolerant Systems. Moscow: Radio & Communication, 1989, 208 p..
- Berger J.M. А Note on Error Detecting Codes for Asymmetric Channels. Information and Control, 1961, vol. 4, issue 1, pp. 68-73, DOI: 10.1016/S0019-9958(61)80037-5
- Freiman C.V. Optimal Error Detection Codes for Completely Asymmetric Binary Channels. Information and Control, 1962, Vol. 5, Issue 1, pp. 64-71, DOI: 10.1016/S0019-9958(62)90223-1
- Efanov D.V., Sapozhnikov V.V., Sapozhnikov Vl.V. Conditions for Detecting a Logical Element Fault in a Combination Device under Concurrent Checking Based on Berger`s Code. Automation and Remote Control, 2017, Vol. 78, Issue 5, pp. 891-901, DOI: 10.1134/S0005117917050113
- Sogomonyan E.S., Gössel M. Design of Self-Testing and On-Line Fault Detection Combinational Circuits with Weakly Independent Outputs. Journal of Electronic Testing: Theory and Applications, 1993, Vol. 4, Issue 4, pp. 267-281, DOI: 10.1007/BF00971975
- Busaba F.Y., Lala P.K. Self-Checking Combinational Circuit Design for Single and Unidirectional Multibit Errors. Journal of Electronic Testing: Theory and Applications, 1994, Vol. 5, Issue 1, pp. 19-28, DOI: 10.1007/BF00971960
- Matrosova A.Yu., Levin I., Ostanin S.A. Self-Checking Synchronous FSM Network Design with Low Overhead. VLSI Design, 2000, Vol. 11, Issue 1, pp. 47-58, DOI: 10.1155/2000/46578
- Ostanin S. Self-Checking Synchronous FSM Network Design for Path Delay Faults. Proceedings of 15th IEEE East-West Design & Test Symposium (EWDTS`2017), Novi Sad, Serbia, September 29 -October 2, 2017, pp. 696-699, DOI: 10.1109/EWDTS.2017.8110129
- Nicolaidis M., Zorian Y. On-Line Testing for VLSI -А Compendium of Approaches. Journal of Electronic Testing: Theory and Applications, 1998, Issue 12, pp. 7-20, DOI: 10.1023/A:1008244815697
- Piestrak S.J. Design of Self-Testing Checkers for Unidirectional Error Detecting Codes. -Wrocław: Oficyna Wydawnicza Politechniki Wrocłavskiej, 1995, 111 p.
- Sapozhnikov V.V., Sapozhnikov Vl.V., Dmitriev A.V., Morozov A.V., Göessel M. Organization of Functional Checking of Combinational Circuits by the Logic Complement Method, Yelektronnoje modelirovanije , 2002, Vol. 24, Issue 6, pp. 51-66..
- Goessel M., Morozov A.V., Sapozhnikov V.V., Sapozhnikov Vl.V. Logic Complement, a New Method of Checking the Combinational Circuits. Automation and Remote Control, 2003, Vol. 64, Issue 1, pp. 153-161, DOI: 10.1023/A:1021884727370
- Saposhnikov Vl.V., Dmitriev A., Goessel M., Saposhnikov V.V. Self-Dual Parity Checking -a New Method for on Line Testing. Proceedings of 14th IEEE VLSI Test Symposium, 28 April -1 May 1996, Princeton, NJ, USA, pp. 162-168, DOI: 10.1109/VTEST.1996.510852
- Dmitriev A., Saposhnikov V., Saposhnikov Vl., Goessel M., Moshanin V., Morosov A. New Self-Dual Circuits for Error Detection and Testing. VLSI Design, 2000, Vol. 11, Issue 1, pp. 1-21, DOI: 10.1155/2000/84720
- Göessel M., Ocheretny V., Sogomonyan E., Marienfeld D. New Methods of Concurrent Checking: Edition 1. -Dordrecht: Springer Science+Business Media B.V., 2008, 184 p.
- Sen S.K. A Self-Checking Circuit for Concurrent Checking by 1-out-of-4 code with Design Optimization using Constraint Don’t Cares. National Conference on Emerging trends and advances in Electrical Engineering and Renewable Energy (NCEEERE 2010), Sikkim Manipal Institute of Technology, Sikkim, held during 22-24 December, 2010.
- Das D.K., Roy S.S., Dmitiriev A., Morozov A., Gössel M. Constraint Don’t Cares for Optimizing Designs for Concurrent Checking by 1-out-of-3 Codes. Proceedings of the 10th International Workshops on Boolean Problems, Freiberg, Germany, September, 2012, pp. 33-40.
- Sapozhnikov V.V., Sapozhnikov Vl.V., Efanov D.V. Design of Self-Checking Concurrent Error Detection Systems Based on "2-out-of-4" Constant-Weight Code. Problemy upravlenija , 2017, Issue 1, Pp. 57-64..
- Sapozhnikov V.V., Sapozhnikov Vl.V. Self-Checking Discrete Devices. St. Petersburg: Energoatomizdat, 1992, 224 p..
- Sapozhnikov V., Sapozhnikov Vl., Efanov D. Concurrent Error Detection of Combinational Circuits by the Method of Boolean Complement on the Base of «2-out-of-4» Code. Proceedings of 14th IEEE East-West Design & Test Symposium (EWDTS`2016), Yerevan, Armenia, October 14-17, 2016, pp. 126-133, DOI: 10.1109/EWDTS.2016.7807677
- Pivovarov D.V. Formation of concurrent error detection systems in multiple-output combinational circuits using the Boolean complement method based on constant-weight codes. Avtomatika na transporte , 2018, Vol. 4, Issue 1, pp. 130-148..
- Sapozhnikov V.V., Sapozhnikov Vl.V., Efanov D.V., Pivovarov D.V. Synthesis of concurrent error detection systems of multioutput combinational circuits based on Boolean complement method. Vestnik Tomskogo gosudarstvennogo universiteta: Upravlenije, vychislitel`naya technika I informatika , 2017, Issue 4, pp. 69-80, DOI: 10.17223/19988605/41/9
- Aksjonova G.P. Necessary and Sufficient Conditions for Design of Completely Checkable Modulo 2 Convolution Circuits. Automation and Remote Control, 1979, Vol. 40, Issue 9, pp. 1362-1369.


