Организация решения задачи исследования операций в MS Excel

Key word: linear and integer programming, transport and problem of assign.

• 1.Задача линейного программирования [1,2].В MS Excel решим задачу:

L ( x ) = 3 x_T + 4 x ₂ ^ max, x_T + 2 x ₂<  4, x_x + x ₂<  3,2 x _t + x ₂<  8, x >  0, i = 1,2

В окне электронной таблицы построим таблицу:

	А	B	C	D	Е	F
1	Задача лин прог-я
2	Переменные	x1	x2
3	значения переменных	2	1
4	целевая функция	3	4		10	0
5	ограничение 1	1	2		4	4
6	ограничение 2	1	1		3	3
7	ограничение 3	2	1		5	8

В ячейки E4,E5,E6,E7 записываем следующие формулы:

E4:=3*B3+4*C3 (целевая функция), E5:=B3+2*C3, E6:=B3+C3, E7:=2*B3+C3 (ограничения ). В ячейках F5:F7 записываем правые части ограничений.

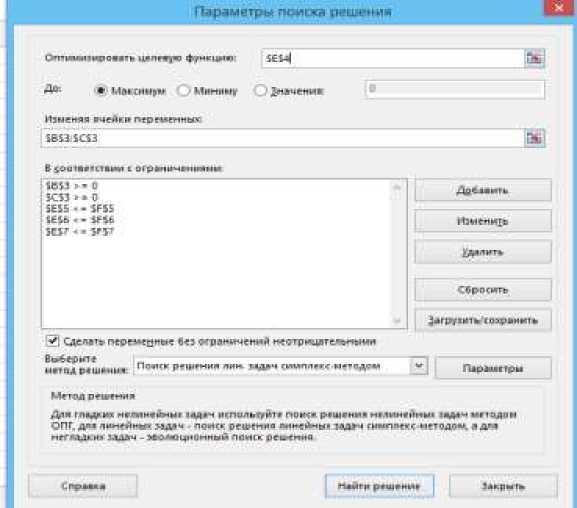
В диалоговом окне Поиск решения задаём значения параметров.

• 1)    в площадке “оптимизировать целевую функцию” задаем ячейку-E4( $E$4).

• 2)    в площадке “изменяя ячейки переменных” указываем ячейки -$B$3:$C$3.

• 3)    в площадке “в соответствии с ограничениями”задаём ограничения задачи.

Нажимая кнопку Найти решение получаем решение задачи. В ячейках В3:С3 даны оптимальное решение, а оптимальное значение L(x) дано в ячейке Е4.

В окне “Выберите метод решение” имеется список трёх методов:

• 1)    Поиск решения задачи линейного программирования симплекс методом.

• 2)    Поиск решения методом ОПГ-для гладких задач,

• 3)    Поиск решения эволюционным методом-для негладких задач..

  

• 2 .    Решение задачу целочисленного линейного программирования. При задании ограничений в диалоговом окне Поиск решение можно потребовать значения переменных, чтобы они были целочисленными. Это требование можно задавать после нажатия кнопку Добавить. Рассмротрим следующую задачу целочисленного программирования:

• 3 .Транспортная задача . Рассмотрим следующую задачу:

L ( x ) = 2 x_x + 4 x ₂ ^max,2 x_x + x ₂<  19/3, x_x + 3 x ₂< 3, x > 0 — целое,i = 1,2

Эта задача решается как и предыдущая задача, с той указанной разницей.

	А	B	C	D	Е	F
1	Задача лин прог-я
2	Переменные	x1	x2
3	значения переменных	1	3
4	целевая функция	2	4		14
5	ограничение 1	2	1		5	6,33
6	ограничение 2	1	3		10	10

В окне Параметры поиска решения задаём следующие параметры:

№	Основные операции	Значения в ячейке таблицы
1	Ячейка значения целевой функции	$E$4
2	Максимум или минимум	Максимум
3	..изменяя значения ячеек	$B$3:$C$3
4	ограничения	$B$3=целое,$B$3>=0,$C$3=целое,$C$3>=0, $E$5<=$F$5,$E$6<=$F$6
5	Способ решения	Симплексный метод

Решение получилось целочисленным: x = ( x , x ₂) = (1,3), L ( x ) = 14 .

L ^{( x} ) = j^ 1L^cu ^x: y ^ ^min, 1L^xy = a i ,1 L ^x ij = b j ,x j >  ⁰ • i = 1 j = 1                        j = 1                i = 1

Здесь принимаем m=3,n=4. В таблице MS Excel имеются 3 пункта отправления (ПО) и 4 пункта прёма (ПП), m<=10,n<=10.

Таблица MS Excel и окно Поиск решения заполняетсяя следующим образом:

• 1)    Матрица платежей рассполагается в диапазоне B3:K12.

• 2)    В ячейках B13:K13 записаны возможности пунктов отправления.

• 3)    В ячейках L3:L12 записаны возможности пунктов приёма (ПП).

• 4)    В диапазоне B14:K23 записаны компоненты плана.

• 5)    В ячейку B24 запишем формулу =сумм(В14:B23), и скопируем ё в ячейки С24:К24.

• 6)    В ячейку L14 запишем формулу =сумм(В14:K14), и скопируем ё в ячейки L15:L23.

• 7)    Значения целевой функции суммируется в ячейке H2: =суммпроизв(В3:К2;В14:К23).

• 8)    Входим в диалоговое окно Данные►Поиск решение , где выбираем значения параметров так: “оптимизировать целевую функцию $H$2 до минимума, изменяя ячейки переменных $B$14:$K$23. В соответствии с ограничениями

$B$24:$K$K24=$B$13:$K$13,$L$3:$L$12:$L$14:$L$23”.

• 9)    На вопрос “Выберите метод решения” выбираем “Поиск решения лин.задач симплекс методом” и нажимается кнопка “Найти решение”. Решение задачи появляется в окне электронной таблицы. Оптимальное значение целевой функции возникает в ячейке H2. Оптимальное решение плана перевозок пояляется в диапазоне В24: К23.

• 4 . Задача о назначении. Эта задача отличается от транспортной

Диалоговое окно Поиск решения заполняется согласно следующей таблице:

№	Основные операции	Значение ячейки
1	Ячейка значения целевой функции	$H$2
2	Максимум или минимум	Минимум
3	..изменяя значения ячейек	$B$14:$K$23
4	Ограничения	$B$24:$K$24=$B$13:$K$13, $L$3:$L$12:=$L$14:$L$23
5	Метод решения	Симплексный метод

Электронная таблица имеет следующий вид:

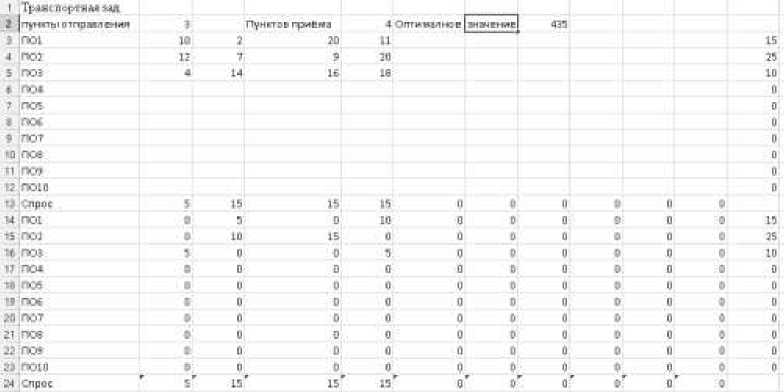
Оптимальное решение получено в ячейках В14:K23, H2.

задачи, тем что здесь a = 1, b = 1, i = 1.. m . j = 1.. n .Изобразим решение на экране:

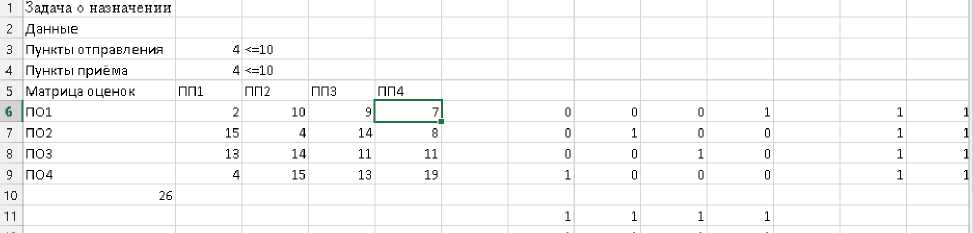
Диалоговое окно Поиск решения заполняется следующим образом:

№	Основные операции	Значение ячейки
1	Ячейка значения целевой функции	$I$A10
2	Максимум или минимум	Минимум
3	..изменяя значения ячеек	$G$6:$J$9
4	ограничения	$G$11:$J$11=$G$12:$J$12, $L$6:$L$9:=$M$6:$M$9
5	Метод решения	Симплексный метод