Организация штамповочного производства при использовании области компромисса

сотрудников в увеличении объёма производства – нужно рассмотреть структуру, в которой будет отражаться взаимосвязь между исследуемыми объектами организационной системы в КТПП.

Для нахождения оптимального финансирования разработаем математическую модель организационной структуры для управления ресурсами, которая представляет матричную структуру взаимодействия (рис. 1).

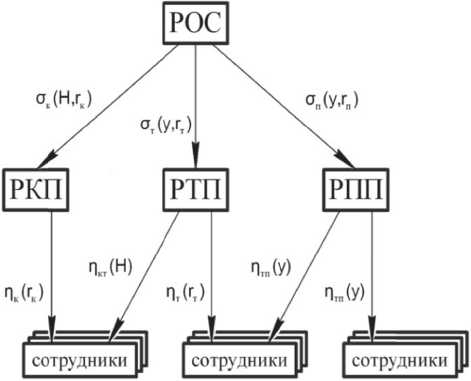
Рис. 1. Матричная структура взаимодействия в КТПП

За основу для моделирования взаимосвязей в организационной системе возьмем работу [10], в которой целевые функции участников, имеют вид:

Фо (^к ( Н . Гк ) ^т ( У . rm ) >^ ( У - Г ) - rK - rm . Г ) =

= D(H, У) -^K ( Н- rK )-^m ( У- rm ) - ^У- rn )- (1)

^Ф к ( ^ к ( ^Н . Г к ) > % ( Г к ) , ^Н >  Г к ) = ^ к ( ^Н , Г к ) - ]^ П К ⁽ У - r K ^ - C K ⁽ Г к ). (2) i = 1

^Ф т ( ^ т ( У^- r m ) ^-П т ( r m ) ^- У ^- Г , ) = ^ т ( У^- r m ) - Т.П т ⁽ r » ⁾ - ^C m ⁽ r m X (3) i = 1

^ф„ ( ^ ( у , г, ) , п „ ( r ) ^, у , r ) = а „ ( у , r „ ) - £ n s ( r , ^{) -} S С , ⁽ r s ), (4) s = 1                 s = 1

f i M ( r i ) ,nL ( H ) , H , r i ) = M ( r i )+C ( H ) - C ( h , t ), i e i , (5)

^f m ( M m ( j M ^j ( У ) ^{, H ,} 1^ =

= n L ( r my n L, ( H )^{- c}m ⁽ H ^, j ^{j e} J^,   (6)

slss  slssslsl fn (nn ( у, rn ) , у, rn ) Mn ( y, rn ) C: (rn ), ^ e ^ ,(7)

где D ( H, y ) - функция дохода организационной системы;

°" , ( ^{Я ,} r : ) ^{, a} m ( У ^, r m ) ^{, O} n ( У ^, r n ) ^- бюджетные Ресурсы, выделяемые конструкторскому (КП), технологическому (ТП) и производственному (ПП) подразделениям со стороны руководителя организационной системы (РОС);

n , ( r : ) ^, M l ( r m ) ^, ^SL C( У ^, r n ) - функции стиму- s = 1

лирования КП, ТП и ПП;

M , _l ( H ) — функция стимулирования i -того конструктора со стороны ТП;

m L _n ( у ) — функция стимулирования j -того технолога со стороны ПП;

n n ( г , ) - функция стимулирования сотрудников s –того ПП;

C : ( Г : ), C m ( Г „ ), S С , ( г , ) - функции затрат КП, s = 1

ТП и ПП соответственно;

c ^sl ( r sl )

^{n v n} ' - функции затрат l -того сотрудника s –того подразделения;

Н – качество (надёжность) изделия;

у – количество изделий;

r_: , r_m , r_n - квалификация, соответственно, конструктора, технолога, сотрудника ПП.

В рассматриваемой модели матричной структуры задача взаимодействия, решаемая с точки зрения руководителя организационной системы, заключается в определении РОС бюджетных средств, побуждающих руководителей функциональных и производственных подразделений выбирать такие стратегии, которые максимизировали бы целевую функцию РОС (1). В свою очередь, руководители функциональных и производственных подразделений при заданных со стороны РОС объёмах бюджетных средств решают задачу определения систем стимулирования своих сотрудников, побуждающих их выбирать такие стратегии, которые максимизировали бы целевые функции РКП (2), РТП (3), РПП (4).

Основная трудность при решении задач взаимодействия заключается в том, что модели принятия решений по выбору параметров организационной системы в ограничениях содержат модели оптимизационных задач нижних уровней. В связи с этим рассмотрим задачи согласованного взаимодействия нескольких двухуровневых систем иерархических систем – задач верхней и нижней иерархии.

Решением задачи взаимодействия является область параметров функции стимулирования, которая наиболее выгодна для РОС. В то же время, эта область позволяет ставить и решать задачи выбора параметров, оптимальных с точки зрения функциональных подразделений и их сотрудников.

Рассчитаем математическую модель задачи согласованного взаимодействия в рассматриваемой организационной системе, на примере машиностроительного предприятия.

Исходными данными для расчёта математической модели послужили данные, полученные в конструкторском (таблицы 1 и 2) и технологическом (таблица 3) отделах машиностроительного предприятия, а также в производственных подразделениях ОАО «Волгабурмаш» (таблица 3).

Таблица 1. Исходные данные для расчёта математической модели принятия решений в конструкторском отделе

Обозначение	Числовое значение	Условные доли
y , шт.	120 шт.	1,2
y 0 , шт.	100 шт.	1
Ay y ,шт.	20шт.	0,2
c , руб.	51000 руб.	1
H	-	0,5
H 0	-	0,4
H - H 0 =Л Я	-	0,5-0,4=0,1

Таблица 2. Исходные данные для расчёта математической модели принятия решений РКП

Обозначение		Числовое значение
Коэффициент правильно принимаемых решений	Р к 1	0,7
	Р к 2	0,5
Уровень квалификации	Г к 1	0,2
	r K 2	0,1
Начальный уровень квалификации	Г к *0	0,15
	Г к 20	0,1
Коэффициент уровня квалификации	b K 1	0,2
	b K 2	0,1
Коэффициент начального уровня квалификации	b l »	0,2
	b /»	0,1
Начальные затраты при базовом уровне надежности	c 1 к 0	0,15
	c 2 ^K 0	0,1

Модель задачи принятия решений РКП:

^Фк ^{( о} к ( H ^{, Г}к ⁾П к ^{( Г}к ^), H ^{, Г}к ⁾ = О_к ( H ^, r_K ) - ^ Х ⁽ H i , ^rK ⁾ - C K ^{( Г}к );

i = 1

о = ^{Р к 1 + в к 2} = ^0,7 + ^0, 5 =

Р к 22

Г н + г_и 0,2 + 0,1

r = _k i    k ² = _z----^ = 0,15;

k 22

,    bk\ + bn 0,2 + 0,1

b =   ---и = _j----_L = 0,15;

k 22

О ( H , r„ ) = в H / r , + br = 0,6 • 0,1/0,15 + 0,15 • 0,15 = 0,4225; K K K K K K

П к 1 ( r k 1 ) = Р к 1 •A H / r k 1 + b k 1 • r k 1 = 0,7 • 01/0,2 + 0,2 • 0,2 = 0,39;

П к 2 ( r k 2 ) = P k 2 •A H / r k 2 + b k 2 • r k 2 = 0,5• 0,1/0,1 + 0,1 • 0,1 = 0,51;

E n K ( H i , r K ) = П к 1 ( r k 1 ) + П к 2 ( r k 2 ) = 0,39 + 0,51 = 0,9;

i = 1

C k 1 ( Г к 1 ) = C K ₀ - b K ₀ ( Г к 1 - r ¹ к 0 ) = 0,15 - 0,2 • (0,2 - 0,05) = 0,12;

C k 2 ( Г к 2 ) = C K ₀ - b 2₀ ( Г к 2 - r ² к 0 ) = 0,1 - 0,15 • (0,1 - 0,025) = 0,08;

C k ( Г к ) = C k 1 ( Г к 1 ) + C k 2 ( Г к 2 ) = 0,12 + 0,08 = 0,2;

E n K ( H i , r K ) + C k ( Г к ) <  О к ( H , Г к );

i = 1

0,9+0,2=1,1>0,4225 - условие не выполняется.

Таблица 3. Исходные данные для расчёта математической модели принятия решений РТП

Обозначение	Числовое значение
Р „ 1	0,5
Р „ 2	0,3
r m 1	0,15
r m 2	0,1
r m 0	0,05
Г2 r m 0	0,025

bm 1	0,2
b m 2	0,1
b m 0	0,1
b m 0	0,05
c 1 m 0	0,2
c 2 m 0	0,1

Модель задачи принятия решений РТП:

^ m ^{( o} m ⁽ y ^, r m ^{) n} m ⁽ r m ^), y ^, r m ⁾ = ^O m ⁽ y ^, r m ^{) -} ^ ^ m ⁽ y ^, r m ^{) -} C m ⁽ r m ⁾;

i = 1

P m =

P m 1 + P m 2 = 0,5 + 0,3

2          2

r m 1 ⁺ r m 2    0,15 ⁺ 0,1

rm = —;— = —;— = 0,125, bm1 + bm 2   0,2 + 0,1

⁷ m =—;— = —;—

O m ( У , r m ) = P m A У / r m + b m r m = 0,4 • 0,2/0,125 + 0,15 • 0,125 = 0,659;

n m 1 ( r m 1 ) = P m 1 ' A У / m + b m 1 ' r m 1 = 0,5 • 0,2 /0,15 + 0,2 -0,15 = 0,7;

n m 2 ( r m 2 ) = P m 2 ' A У / r m 2 + b m 2 ' r m 2 = 0,3 • 0,2/0,1 + 0,1 • 0,1 = 0,61;

E ^ m ⁽ y , r m ⁾ = ⁿ m 1 ⁽ r m 1 ^{) + n} m 2 ⁽ r m 2 ⁾ = ⁰,^{7 + 0},⁶¹ = V¹; i = 1

C m 1 ( r m 1 ) = C m ₀ + b m ₀ ( r m 1 - r ¹ m 0 ) = 0,2 + 0,1 • (0,15 - 0,05) = 0,205;

C m 2 ( r m 2 ) = ^о + b m ₀ ( r m 2 - r ² m 0 ) = 0,1 + 0,05 • (0,1 - 0,025) = 0,104;

C m ( r m ) = C m 1 ( r m 1 ) + C m 2 ( r m 2 ) = 0,205 + 0,104 = 0,309;

E ^ m ⁽ H ^, r m ^{) +} C m ^{( r} m ⁾<  ^O m ^{( H , r} m ^ i = 1

Таблица 4. Исходные данные для расчёта математической модели принятия решений РПП

Обозначение	Числовое значение
Д , 1	0,3
P n 2	0,2
rn 1	0,2
rn 2	0,1
г1 r n 0	0,2
2 r n 0	0,1
bn 1	0,05
b n 2	0,2
b\	0,1
b2n0	0,1
c 1 n 0	0,4
C n 20	0,2
Pn0	0,2
p^	0,1

1,31+0,309=1,619>0,659 - условие не выполняется.

Модель задачи принятия решений РПП:

2                 2

^ n ^{( o} n ( y , r n ^{) П} П ( y , r n ⁾ , y , r n ⁾ = ^O n ( y , r n ⁾ - Z ^ n ( y , r n ⁾ - Z C n ( r n )’ i = 1                  i = 1

2                  2

O n ⁽ У ^, r n ⁾ = Z P n A y ^/ r n ⁺ Z b n r n = 0,75; s = 1                   s = 1

П п 1 ( r n 1 ) = в n 0 ■ ( r n 1 - r ¹ n 0 ) = 0,2 ■ (0,2 - 0,1) = 0,02;

П 2 ( r n 2 ) = в ²¹ n 0 ■ ( r n 2 — r ²¹ n 0 ) = 0,1 ■ (0,1 - 0,05) = 0,005;

Z П п ( r n ) = П п 1 ( r n1 ) + П п 2 ( r n 2 ) = 0,02 + 0,005 = 0,025;

i = 1

C n 1 ( r m 1 ) = C П ₀ + b П ₀ ( r n 1 - r ¹ n 0 ) = 0,4 + 0,1 ■ (0,2 - 0,1) = 0,41;

C n 2 ( r n 2 ) = C 2₀ + b n ₀ ( r n 2 - r ² n 0 ) = 0,2 + 0,1 ■ (0,1 - 0,05) = 0,205;

Z C n ( r n ) = C n 1 ( r n 1 ) + C n 2 ( r n 2 ) = 0,41 + 0,205 = 0,615;

s = 1

2              2

Z ^{n (}^⁺ Z C n ⁽ r n ⁾ <  O ⁽ y ^, r n ⁾ ;

i = 1               s = 1

0,025+0,615=1,64>0,75 - условие выполняется.

При анализе матричной модели принятия решения РКП и РТП было выявлено, что для выполнения условия принятия решения не нужен сотрудник высокой квалификации, так как с задачами сможет справиться менее опытный специалист.

Произведем расчет с уменьшенными значениями коэффициентов квалификации.

Таблица 5. Исходные данные для скорректированного расчета математической модели принятия решений РПП

Обозначение	Числовое значение
Р к 1	0,1
Р к 2	0,075
Г к 1	0,175
Г к 2	0,15
Ь к 1	0,15
Ь к 2	0,1

П к 1 ⁽ r k 1 ) = P к 1 ■ ^{A H/} r k 1 ^{+ b}k 1 ■ Г ! =

= 0 , 1 ■ 0 , 1 / 0 , 175 + 0 , 15 ■ 0 , 175 = 0 , 0834 ;

П к 2 ⁽ r k 2 ) = P к 2 ■ ^A H ^/rk 2 ⁺ b k 2 ■ Г 2 =

= 0 , 075 ■ 0 , 1 / 0 , 15 + 0 , 1 ■ 0 , 15 = 0 , 065 ;

Z ^ К (Ht^) = П к 1 ⁽ Г 1 ) ⁺ П к 2 ⁽ Г 2 ) =

= 0 , 0834 + 0 , 065 = 0 , 1484 ;

Z n К (H , ,r K ) + С к (r) к (Н,Г к ); = 1

0,1484+0,2=0,3484≤0,4225 - условие выполняется.

Таблица 6. Исходные данные для скорректированного расчета математической модели принятия решений РТП

Обозначение Числовое значение Рт1 0,1 Рт 2 0,075 Ьт 1 0,1 Ьт 2 0,05 n m 1 ( rm 1) = P m 1 'Ay/rm 1 + bm 1 ■ rm 1 =

= 0 , 5 ■ 0 , 2 / 0 , 15 + 0 , 2 ■ 0 , 15 = 0 , 7 ;

П m 2 ⁽ r m 2 ) = P m 2 '^A У / r m 2 ^{+ b} m 2 ■ r m 2 =

= 0 , 3 ■ 0 , 2 / 0 , 1 + 0 , 1 0 , 1 = 0 , 61 ;

]E П m ⁽y^,r m ) = n m 1 ⁽r m 1 ) ⁺ n m 2 ⁽Г п 2 ) =

= 0 , 7 + 0 , 61 = 1 , 31 ;

Z n 'm (H.r‘) + € m (r , ) , (H,r , );

i = 1

0,303+0,309=0,612<0,659 - условие выполняется.

Полученные в ходе расчетов результатов сведем в таблицу 7.

Таблица 7. Сводная таблица результатов

Значение	σ k	σ m	σ n
Расчетное значение	0,4225	0,659	0,75
Скорректированное значение	0,3484	0,612	0,64

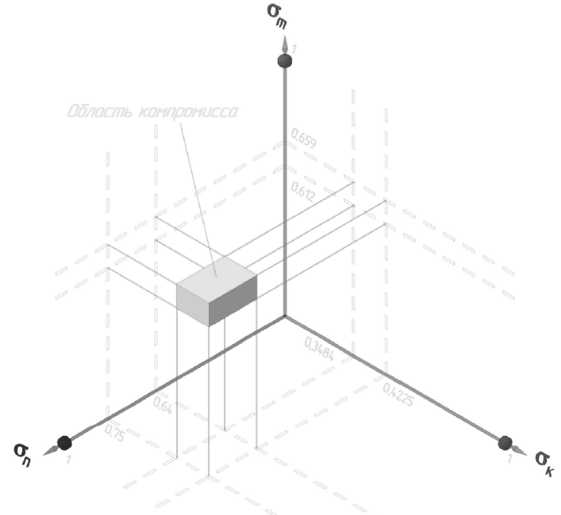
Рис. 2. Область компромисса при принятии согласованных решений в КТПП

По данным значениям построим график (рис. 2), где определим область, которая будет яв-   2.

ляться для всех оптимальной (область компромисса) при принятии согласованных решений в конструкторско-технологической подготовке производства (КТПП) на уровне руководителей подразделений.

Разработанная модель согласованного вза-   3.

имодействия участников КТПП является удобным средством для принятия решений при повышении надёжности изделий. Она позволяет

устранить противоречия между конструкторским, технологическим и производственным подразделениями на уровне руководителей. На 4 графике наглядно видны значения бюджетных . ресурсов (средств), выделяемых руководителем организационной системы (РОС). Обозначена область компромисса, выход из какого-либо подразделения влечет затруднения и появления противоречий при принятии согласованных ре-  5.

шений в целях повышения надежности.