Осаждение двух твердых частиц, покрытых жидкой оболочкой

В многочисленных работах [4] в стоксовом приближении рассматривается задача об осаждении двух жидких сфер или двух твердых сфер в вязкой жидкости. На практике часто встречаются составы, в которых твердые частицы находятся в жидкой оболочке. Поэтому представляет интерес случай, когда под действием силы тяжести осаждаются твердые частицы, покрытые слоем жидкости, вязкость которой отлична от вязкости несущей среды.

Пусть в вязкую несжимаемую жидкость вязкости Д/ помещены две твердые сферические частицы А и В одинакового радиуса Ь, окруженные слоем другой несжимаемой жидкости с вязкостью r]d. Жидкая оболочка имеет сферическую форму радиуса а. Остановимся на случае, когда вектор г, соединяющий центры частиц А и В, параллелен вектору ускоре ния свободного падения д (частицы двигаются вдоль линии, соединяющей их центры). Используя результаты [1 — 3], получим, что скорость частицы А иА'---L-

4^ К

. L

1--Е +

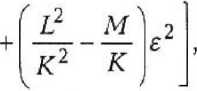
где ( — сила, действующая на частицу; К, L, М — коэффициенты, вычисленные в [2]; е — отношение радиуса жидкой оболочки к расстоянию между частицами.

Ввиду громоздкости выражений для скалярных коэффициентов рассмотрим частные случаи движения частиц. Зададим следующие значения параметров: а = 10“² см, b = 0,5 10^-2 см, ?^ = = 1 г/(см с), ^ = 0,5 г/(см с),

Pl = 1 г/см³, p_d = 0,8 г/см³, p_p = 5 г/см³ Здесь введены обозначения: р[ — ллот-тюстыгесущей жидкости, p_d — плотность жидкой оболочки, окружающей частицу, рр — плотность частицы.

Чтобы установить величину силы тяжести, найдем среднюю плотность частицы р Из выражения следует, что р = pd + ^рр - Pl ^ а

Для принятых значений параметров имеем р = 1,325 г/см³

Сила, действующая на частицу, равна по величине разности силы тяжести и силы Архимеда:

f = (р - pi)g - —ля³ = 1,335491 -10”⁸ Н.

Для заданных выше значений параметров получим, что скорость частицы А в этом случае

С/^л|1 = 0,0084536 + 0,0130271 е +

+ 0,0221584 f 2 см/с.

На рис. 1 представлена зависимость скорости частицы А от е. Анализ численных результатов показывает, что скорость осаждения частиц, покрытых жидкой оболочкой, больше скорости осаждения твердых частиц, по меньше скорости жидких капель того же размера.

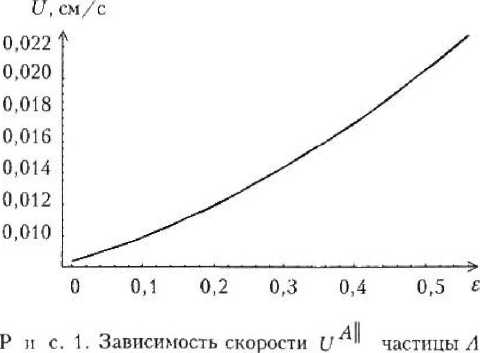
от параметра £

Возьмем случай, когда вектор г перпендикулярен вектору ускорения свободного падения д (частицы двигаются перпендикулярно линии, соединяющей их центры). Скорость частицы А с точностью ДО Е

U^A1 = --(1- — fl   (2)

4miiN\ N J где А, ^ — коэффициенты, вычисленные в [3].

Рассмотрим частные случаи движения частиц. Зададим те же значения параметров: а = 10~² см, b = 0,5 10~² см, Ц/ = 1 г/(см • с), g_d = 0,5 г/(см с), Pl = 1 г/см³, p_d = 0,8 г/см³, Рр = = 5 г/см³ Средняя плотность частицы найдена выше и составляет р = = 1,325 г/см³ Сила, действующая на частицу в этих условиях,

/= 1,335491 10"8Н.

Для заданных значений параметров скорость частицы А

U ^{л 1} = 1,335491 Ю^О.06330 +

+ 0,06581с) см/с.

На рис. 2 приведена зависимость скорости частицы А от расстояния между частицами Е. Согласно анализу численных результатов скорость осаждения частиц, покрытых жидкой оболочкой, больше скорости осаждения твердых частиц, но меньше скорости жидких капель того же размера.

U, см/с

0,0120 “

0,0115 .

о.оыо :

0,0105

0,0100

0,0095

0,0090

0,0085 Vz—----------------------------^.

0          0,1       0,2        0,3     0,4 е

Рис. 2. Зависимость скорости Ц частицы А от параметра г

В случае произвольного расположения частиц, скорость осаждения можно представить в виде двух составляющих — движения вдоль и перпендикулярно линии, соединяющей центры частиц. Каждая из составляющих вычисляется по формулам (1), (2), где вместо силы тяжести ( подставляется составляющая, направленная вдоль или перпендикулярно вектору г.

БИБЛ И О ГР АФИЧ ЕСКИЙ СПИСОК

• 1.    Мартынов С. И. Гидродинамическое взаимодействие двух капель, содержащих твердые частицы / С. И. Мартынов, О. А. Петухова / / Тр. Средневолж. мат. о-ва. Саранск, 2002. Т. 3 — 4, № 1. С. 246 - 249.

• 2.    Петухова О. А. Математическая модель взаимодействия частиц, покрытых жидкой оболочкой / О. А. Петухова; Средневолж. мат. о-во. Саранск, 2002. 35 с.

• 3.    Петухова О. А. Обтекание линейным потоком двух капель, содержащих твердые частицы / О. А. Петухова // Вести. Морд, ун-та. 2002. № 1 —2. С. 122 — 125.

• 4.    Хампель Дж. Гидродинамика при малых числах Рейнольдса / Дж. Хаппель, Г. Бренер. М.: Мир, 1971. 631 с.

Поступила 18. / 0.04.