Oscillation of bonds in solid and liquid phases of substance and phase transitions
Автор: Cheredov V.N., Askhabov A.M.
Журнал: Вестник геонаук @vestnik-geo
Рубрика: Научные статьи
Статья в выпуске: 9 (285), 2018 года.
Бесплатный доступ
We propose a new approach to describe the structure of substance suggesting an oscillatory nature of interatomic (intermolecular) bonds. This approach develops a model of thermal oscillations and significantly expands possibilities for analysis and understanding of phase transitions. We revealed a temperature dependence of dynamics of the lattice of the bonds and its change in the process of phase transitions. By example of water we obtained data for the quantitative characterization of stable bonds at various temperatures.
Intermolecular bonds, phase transitions, crystallization, lattice structure, model of oscillating bonds
Короткий адрес: https://sciup.org/149128718
IDR: 149128718 | УДК: 548.52 | DOI: 10.19110/2221-1381-2018-9-46-49
Текст научной статьи Oscillation of bonds in solid and liquid phases of substance and phase transitions
Introduction A situation may occur, when a part of the bonds be-
The problems of the structural organization of substance attract attention of physicists, chemists and material scientists. These problems are particularly relevant because of recent intervention of science into the world of nanostructures and need to develop new ideas to describe the nanoscale substance. In recent years, original models of the organization of substance at the nanoscale have been developed to solve a wide range of problems in crystallography, mineralogy and related sciences. Such an approach proved to be especially effective to analyze a wide range of problems associated with phase transitions, nucleation and growth of crystals [1].
In this paper we suggested a model of intermolecular oscillating bonds to study the bond structure of crystalline and liquid phases of substance, the first order phase transitions. This model significantly expands our ability to analyze phase transitions, to understand the nature and structure of the condensed state of substance.
Oscillating bond model
We shall consider a homogeneous section of a solid or liquid phase in a hypothetical state, when all bonds between molecules (atoms) are stable. Let this area of the substance receives a certain small amount of heat Δ Q . Then the internal energy of the molecules increases by the same amount Δ Ei= Δ Q . It is quite natural to assume that the increase of the internal energy of molecules can lead to breaking certain in-termolecular bonds.
Generally the breaking of a bond can be represented as a temporary redistribution of the electron density of the atoms, forming molecules and participating in the bond, to the state of lack of bond. For example, for hydrogen and van der Waltz bonds, the breaking of bonds between molecules means a temporary change of the electron density, at which one of the molecules, participating in the bond, loses dipole properties for some time [2].
tween molecules in the structure of substance is in a stable state, and a part — in a broken state. If the substance is in a state with constant temperature and pressure, i. e. with the same total internal energy of the molecules, the part of the intermolecular is always in a broken state. Broken bonds are restored and transit into a stable state, and other stable bonds are broken at the same time. There is, as it were, a «flicker-ing» of breaking bonds or oscillation of bonds within the substance. Earlier, we considered the oscillating character of interatomic bonds as a property inherent only to nanoscale clusters and impossible for the macrostate of substance [1, 2].
From the homogeneity of space it follows that the distribution of broken bonds in space and time should be homogeneous. Each intermolecular bond in the volume of substance breaks from time to time and then occurs again, i. e. oscillates.
With further increasing internal energy of the molecules, the number of broken bonds of H molecule increases and, accordingly, the number of stable bonds of F molecule decreases ( F + H = Km , where Km is the coordination number of the molecule).
A specific intermolecular bond is in two states. Part of the time τ f the bond is stable, while part of the time τ g it is unstable or broken, while the bond flickering time τ m= τ f+ τ g. In this model, all intermolecular bonds oscillate. The internal energy of substance at a specific moment of time is determined solely by the number of stable or the number of broken bonds, and the state of substance itself or its internal energy is determined by the instantaneous «snapshot» of all lattice bonds (Fig. 1). At each subsequent moment of time, the structure of the bonds of substance changes.
This model presents objects of substance, which entire volume is in the same thermodynamic state, excluding heterogeneities of both the substance and its state. In other words, if the entire object is heated (or cooled), then all
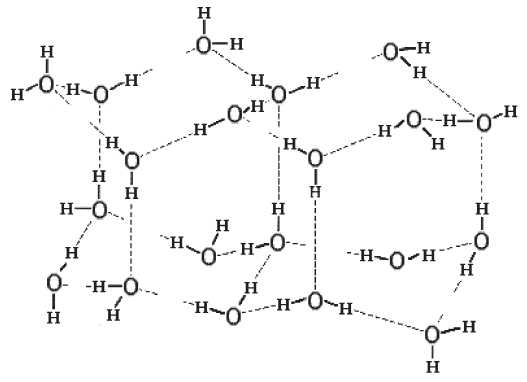
Fig. 1. Instantaneous structure of ice with a hexagonal lattice with oscillating bonds. Intramolecular, intermolecular and broken intermolecular bonds are shown by a straight line, dotted and broken by a dashed line, respectively. This figure has been taken from minor work [3]
Ðèñ. 1. Ìãíîâåííàÿ ñòðóêòóðà ëüäà ñ ãåêñàãîíàëüíîé ðåøåò-êîé ñ îñöèëëèðóþùèìè ñâÿçÿìè. Âíóòðèìîëåêóëÿðíûå, ìåæìîëåêóëÿðíûå è ðàçîðâàííûå ìåæìîëåêóëÿðíûå ñâÿçè ïîêàçàíû ïðÿìîé, ïóíêòèðíîé è ðàçîðâàííîé ïóíêòèð-íîé ëèíèåé ñîîòâåòñòâåííî. Äàííûé ðèñóíîê ñ íåáîëüøèìè èçìåíåíèÿìè âçÿò èç ðàáîòû [3]
parts of the object are heated (or cooled) equally. If the object moves from one phase of substance to another, then each part of it simultaneously moves from the same phase to another. This limits the objects of consideration to areas of one phase during phase transitions or to the value of thickness of the phase transition boundary (crystallization front), i. e. to nanoscale.
On the surface of a solid and liquid phase of substance, the number of broken bonds of molecules is much greater than in the volume of substance. Accordingly, the number of stable bonds of molecules in the surface layer of a substance is less than that of volume molecules. This results in the difference in the thermodynamic properties of substance on surface and in volume. In particular, the melting point of thin films is lower than in the volume of substance. Accordingly, the solid body begins to melt on its surface.
In the solid aggregate state of substance, each molecule (atom) has at least 3 stable intermolecular bonds at a given time. Three unbroken intermolecular bonds for one molecule is quite sufficient for its stable position in the structure of a solid and for the structure to maintain a stable lattice. If there are molecules with a number of stable intermolecular bonds of less than 3, a phase transition from the solid state to the liquid state can occur and vice versa. Generally the converse is not true.
In the liquid aggregate state of substance, each molecule (atom) has at least 2 stable intermolecular bonds. If there are molecules with the number of stable intermolecu-lar bonds of less than 2, a phase transition of the liquid aggregative state of substance into the gaseous one occurs and vice versa.
Depending on how many bonds of the molecule at a given time are in the stable and how many are in the broken state, the molecule occupies a more or less excited equilibrium state (position in the structure), characterized, respectively, by a greater or smaller value of the internal energy of the molecule. At that under the influence of remain- ing bonds of the neighboring molecules, the molecule itself slightly shifts in space. When restoring the bond, i. e. when acquiring a stable bond, the molecule again occupies its original spatial position and transits into a less excited state with less energy.
The same happens when all the other bonds of the given molecule oscillate. It should be considered that the molecules, which the selected molecules have bonds with, also oscillate around the equilibrium position during oscillation of their bonds. This gives the vibrations of a molecule a chaotic character with degrees of freedom corresponding to the degrees of freedom of thermal vibrations.
The temperature of substance affects the oscillation of bonds of molecules of the liquid and solid phases. Hence we assume that the number of oscillating bonds in the broken state in the total number of bonds is constant and determined, first of all, by temperature T and, accordingly, by internal energy of molecule Åi . The more T, the more H and the less F .
For molecules of substance at Ò = 0 K , to be released from intermolecular bonds, it is necessary to impart energy, referred to as sublimation energy Es and equal to:
i E
Es= 2^B^b ~*~ ^Qm + ^Qb = Km^- , (1)
where i — number of degrees of freedom of the sublimated molecule, kB — Boltzmann constant, Tb — boiling point, Δ Qm — heat of fusion per one molecule, Δ Qb — heat of vaporization per one molecule, Km — coordination number of the molecule in the solid phase, Em — energy of breaking of one bond at T = 0 K .
Formula 1 shows what energy the substance in the solid phase should gain at the absolute zero temperature, so that all molecules become free and the molecule from the solid phase transits into gaseous, that is, it becomes free from in-termolecular bonds. The sublimation energy is equal to the bond energy of the molecule at zero temperature. The division by 2 on the right side of Formula 1 arises due to breaking of one bond refers directly to two molecules. According to Formula 1 we can calculate energy of breaking of one bond of a molecule.
The binding energy of molecule Eb= FEm= (Km– H) Em will be determined by the formula:
-
F -^- = Eb = Es — Ei = Km—--Ei . (2)
For the solid phase the internal energy of molecules is determined by the energy of their thermal vibrations (energy of formation and dynamics of defects in the crystal lattice [4] are neglected, since it is much less than the latter). To determine the energy of thermal vibrations of molecules we use the Debye model [5].
Then, the bond energy of molecules of the solid phase is determined by the following formulas:
where F sp — amount of stable molecular bonds in the solid phase at temperature Ò , Θ D — Debye temperature.
At the melting temperature T = Tm Formula 3 allows calculating the number of stable bonds of the molecule in the solid phase at the melting temperature Fm from the expression for the bond energy:
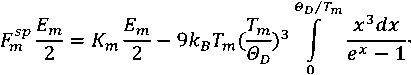
where — number of stable bonds of the molecule in the solid phase at the melting temperature T = Tm .
Substituting the constants and known data into Formula 4 we obtain the number of stable bonds of the molecule in the solid phase at the melting point At the melting point in the solid phase the molecule has stable bonds, and therefore bonds are broken.
In the liquid phase at the melting point (crystallization), the heat of melting (reduced to one molecule) should be subtracted from the expression of the bond energy in Formula 4. Accordingly we obtain the number of stable bonds of the molecule in the liquid phase at the melting point :
, (5)
where — number of stable bonds of the molecule in the liquid phase of water at the melting point
Tm
.
For the gaseous phase it is necessary to take into account the heat of vaporization, reduced to one molecule. To do this we substitute Formula 1 into Formula 2. We obtain the formula for the bond energy of the gaseous phase molecule at the boiling point
Ò = Tb
:
F F i , (6)
where — number of stable bonds of the molecule in the gaseous phase at the boiling point
Ò = Tb ( = 0)
.
In the liquid phase at boiling point: , (7)
where — number of stable bonds of the molecule in the liquid phase at the boiling point
Ò = Tb
.
In the liquid phase, for
Tm< T < Tb
the number of stable bonds of the molecule varies in the following range , at that with increasing temperature the number of bonds decreases. Since thermodynamics lacks a complete model of the internal energy of liquid molecules, therefore we approximate the function of the internal energy of the liquid phase with temperature by a linear dependence, especially since in real liquids, for example, water, it is close to linear. Then for the number of stable bonds of the molecule we obtain the following formula:
F1^ = Flp — 1 1 m T — T 1 1m ,
where — number of stable bonds of the molecule in the liquid phase at temperature
Tm Formula 8 introduces the value of characteristic tem- perature difference of the liquid phase of substance, which is determined by the following relationship: A0 C^ 17^ _ T7^ b The characteristic temperature difference of the liquid phase of substance is the temperature difference, with the increase by which the temperature of liquid from the temperature of melting, exactly one intermolecular bond of the molecule should break. This characteristic temperature difference is also introduced in the present work and is a unique parameter for each substance.
For convenience and clarity we introduce two indicators: fraction of stable bonds of molecules
f = F/Km
and fraction of broken bonds of molecules
h = H/Km.
The coordination number corresponds to the coordination number of molecules in the corresponding phase, i. e. for molecules of the solid phase
Km
, in the liquid phase (may be more and less than
Km
), in the gaseous phase = 0. The range of change of the indices
f
and
h
is defined from 0 to 1. AT that always
f + h = 1
.
The results for water are presented in the graph (Fig. 2).
Fig. 2.
Phase transitions and temperature dependence of the number of stable bonds of
F
molecules for
Í2Î
molecules: à — crystals of hexagonal ice, á — water, â — pairs, where
Kp
is the percolation threshold of water molecules, — the number of stable molecular bonds in liquid phase of water at the melting temperature
Tm
Ðèñ. 2.
Ôàçîâûå ïåðåõîäû è òåìïåðàòóðíàÿ çàâèñèìîñòü êîëè-÷åñòâà óñòîé÷èâûõ ñâÿçåé ìîëåêóë
F
äëÿ ìîëåêóë
Í2Î
: a — â òâåðäîé ôàçå, b — â æèäêîé ôàçå, c — â ãàçîîáðàçíîé ôàçå, ãäå
Kp
— ïîðîã ïåðêîëÿöèè ìîëåêóë âîäû, — êîëè÷åñòâî óñòîé÷èâûõ ñâÿçåé ìîëåêóëû â æèäêîé ôàçå âîäû ïðè òåìïå-ðàòóðå ïëàâëåíèÿ
Tm
The necessary quantitative data on water are taken from [6–8]. Calculations on formulas 4, 5, 7 give for water the following values of number of stable bonds for ice at the melting temperature = 3.64. At the melting temperature in ice, the molecule has 3.64 stable bonds, and therefore 0.36 bonds are broken. In the liquid phase at the melting temperature (crystallization) for water, we get = 3.22. In the liquid phase, at boiling point for water, value = 2.84 is obtained. Conclusion For the first time we present a model of oscillating bonds, within which a model of the structure of a crystal and liquid is constructed as a continuous oscillating network of bonds, which is homogeneous by the number of stable inter-molecular bonds. We revealed the temperature dependence of number of stable molecular bonds for the solid and liquid phases, changes during the first order phase transitions «solid-liquid» and «liquid-gas». By example of water we showed the dependence of number of stable intermolecular bonds on the temperature and phase of substance, its change during phase transitions.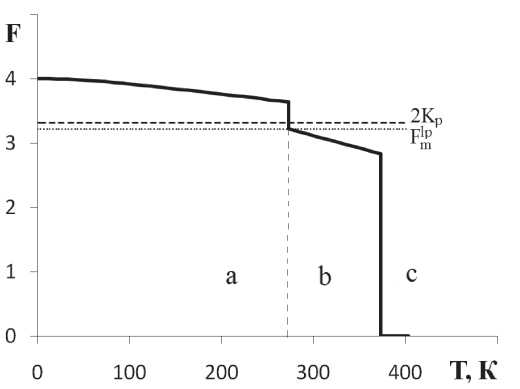
Список литературы Oscillation of bonds in solid and liquid phases of substance and phase transitions
- Ashabov A. M. Nanoklasternaya model obrazovaniya zhidkoi vody (Nano-cluster model of formation of liquid water). Proceedings of Komi Science Center UB RAS, 2016, No. 1(25), pp.62-67.
- Kaplan I. G. Mezhmolekulyarnye vzaimodeistviya. Fizicheskaya interpretatsiya, komp'yuternye raschety i model'nye potentsial (Intermolecular interactions. Physical interpretation, computer calculations and model potentials) Moscow: BINOM. Laboratorija znanij, 2012, 400 pp.
- Finkelstein A. V., Ptitsin O.B. Fizika belka (Physics of the protein). Moscow: KDU, 2012, 456 pp.
- Cheredov V.N. Statika i dinamika defektov v sinteticheskih kristallah flyuorita (Statics and dynamics of defects in synthetic fluorite crystals) Saint-Petersburg: Nauka, 1993, 112 pp
- Landau L. D., Lifshitz E. M. Statisticheskaya fizika (Statistical physics). Part 1. Moscow: Fizmatlit, 2010, 616 pp.
- Enochovich A. S. Spravochnik po fizike i tehnike (Reference book on physics and techniques) Moscow: Prosveshenie, 1989, 224 pp
- Zatsepina G. N. Fizicheskie svoistva i struktura vody (Physical properties and structure of water) Moscow: Moscow State University, 1998, 184 pp.
- Eisenberg D., Kautsman V. Struktura i svoistva vody (Structure and properties of water). Moscow: Direct-Media, 2012, 284 pp.


