Осцилляции поперечной магнитопроводимости графена

В последнее время ведется интенсивное теоретическое [1;2;3] и экспериментальное [4;5;6;7] исследование свойств графена, представляющего собой монослой углерода. Связано это, во-первых, с тем, что графен обладает рядом необычных свойств, обусловленных особенностями его зонной структуры [8;9], а во-вторых, с тем, что этот материал получен в лаборатории совсем недавно [10]. Возможность проявления ряда нелинейных кинетических эффектов в графене связана с непараболичностью и неаддитивностью его энергетического спектра. Например, нелинейный электромагнитный отклик в графене исследован в [1]. Возможность выпрямления поперечного тока, в графе -не изучена в [2].

В [10] экспериментально показано, что длина, свободного пробега электрона в графене имеет порядок микрометра. Этот факт позволяет использовать графен для создания микрометровых приборов, работающих в баллистическом режиме. Высокая электрическая проводимость делает графен перспективным материалом для использования в наноэлектронике наряду с углеродными нанотрубками [11].

Кроме этого, энергия электрона проводимости в зоне Бриллюэна вблизи так называемой дираковской точки пропорциональна. модулю квазиимпульса, подобно энергии безмассовых частиц [9]. Эта. особенность энергетического спектра позволяет, кроме всего прочего, использовать графен для проверки релятивистких эффектов.

В [12;13;14;15] изучены магнитные осцилляцион-ные эффекты в графене вблизи дираковской точки. Влияние магнитного поля на высокочастотную проводимость графена и на поглощение графеном электромагнитного излучения исследованы в [7;13;14;15]. Эффект Шубникова-де Газа, в двумерной системе с дираковским спектром изучены в [12], где предполагалось, что уровни Ландау имеют конечную ширину, связанную с рассеянием носителей заряда на неоднородностях решетки. При этом не рассматривался конкретный механизм рассеяния, а уширение уровней Ландау вводилось как феноменологический параметр.

В данной работе рассмотрены осцилляции магнитопроводимости графена, помещенного во внешнее магнитное поле, с учетом упругого рассеяния электронов проводимости на акустических фононах. В случае, когда графен помещен во внешнее магнитное поле, напряженность H которого перпендикулярна, его плоско- сти, гамильтониан имеет вид [3]

H = hu _   _

0 F -±-i±+

( dy   dx aH d .8 y)

--i 1—2~ d y dx a_H

где υ _F – скорость электрона на поверхности Ферми, a_H = c h eH – ларморовский радиус. Собственные волновые функции и значения энергии оператора (1), имеют вид (Там же)

| kn =

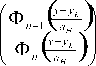
если n >  0 ;

1      e ikx

2 La_H

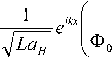
0 )

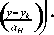
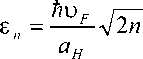
• (2)

• (3)

где ф n ( y ) — функция гармонического осциллятора, k — проекция волнового вектора, электрона, на. ось О_х, y_k = - ka H , n = 0,1, 2,... , L — линейный размер графена. вдоль оси O x . Из (3) видно, что уровни Ландау в графене не являются эквидистантными.

Тот факт, что движение электронов проводимости вблизи дираковской точки нельзя описывать в приближении эффективной массы, требует пересмотра формулы Титейка. Для этого воспользуемся подходом, развитым в [16]. Пусть вдоль оси Oy приложено слабое электрическое поле E. Плотность тока для ансамбля частиц, описываемого матрицей плотности , определяется формулой jy = -eТТkn|р|kn')(kn'Idy\n • kn k ′n′                           dt

Матричный элемент оператора скорости электрона в графене при наличии квантующего магнитного поля вычисляется между волновыми функциями (2) и имеет вид

(kn '14 \Ц = - i U f (6 „ , 1 +8 „->, . , • d t

Подставляя (5) в (4), получаем:

j y

= ie uF ^( kn |p| kn +1) + ^kn| p| kn -1^ )•

nk

Полная матрица плотности ρˆ_T , учитывающая переходные процессы, определяется из уравнения движения:

ˆ

- i h ∂ ρ ^T = ρˆ H - H ρˆ ,

∂ t      ^{T T}

где H ˆ – гамильтониан, учитывающий внешнее магнитное поле, тянущее электрическое поле и потенциал рассеяния v ( r ) :

представить в следующем виде [17]:

V ⁽ r ) = Е V exp ( ^z ' q • ^r ) , ^q

где V = h h / V q2 p vS , q — волновой вектор акустических фононов, Λ – деформационный потенциал, ρ – поверхностная плотность графена, ν – скорость звука в графене, S – площадь образца. После подстановки

(15) в (13) получаем:

H = H 0 + eEy + V ( r ) .

σ yy =-^{π e 2} ∑∑∑ A n V q ^{2 ∂ f} ( y k ′ - y k ) ² k ′ n ′ e^{i q ⋅ r} kn ² δ ( ε n ′ -ε n ) .         (16)

h nk n ′ k ′ q ∂ε n

Перейдем к лапласовскому образу матрицы плотности P ( s ) с помощью интегрального преобразования:

После вычисления матричного элемента и сумм, входящих в формулу (16), получаем следующее выражение для магнитопроводимости:

to

P ( s ) = s J e - st p _T ( t ) d t .

e ² Λ ²

σ _yy = -      ₃ ∑∑

16πρ v a_H ³ nn ′

n

Перепишем уравнение (7) для p ( _s

A      A A      A A                                                          A. x

- i h sP = PH - HP - i h s ρˆ₀,                  (10)

где ρˆ₀ – матрица плотности в начальный момент времени (до включения электрического поля). В качестве начальной матрицы плотности выберем точную матрицу равновесного ансамбля:

^где F ( n ) = A n / л⁴Q n ( x ) d x ,

^Qn ⁽ x ) = (Ln - 1 ⁽² ^У L n ⁽7²⁾⁾ exp ( - ^{X 2} /2 . ,

k к n '|p₀| kn = f ( 8 _n > „. „ 5 к k ,

L_n (x )

ⁿ — полином Лагерра. Если осцилляции проводимости малы по сравнению с неосциллирующей частью, то их можно учесть только в одной из сумм (17). Воспользовавшись формулой Пуассона, преобразуем (17) следующим образом:

где f ( 8 n ) — функция распределения Ферми-Дирака. Матрица плотности ρˆ , описывающая стационарный ток и входящая в формулу (6), определяется спустя столь долгий промежуток времени, что все величины, характеризующие переходные процессы, обращаются в нуль. Значение матрицы плотности спустя длительный промежуток времени можно определить, найдя предел, к которому стремится образ Лапласа, p ( s ) , когда, параметр s → 0 .

В борновском приближении по потенциалу рассеяния V ( г ) и в линейном приближении по напряженности электрического поля получаем:

²²        го ”.

c yy = - e^- -13- У [f ( n ( e )) f | — I e^{n (E)}d _e       (18)

16npv a3H K~-TO 0         de (de J           , V / где n(s) определяется из (3). Подставив в (18) функ цию распределения Ферми-Дирака, получим:

°

e ² Л²

64n h ⁴ p v u ^ 6

_w *        / 2 2 \                  ⁿ i ^ a h ^E 2

«„У f= 2 F I aH^r I ch - 2      e ^{h u F} d^ , (19)

^H K : :* 0     (2 h 2 u F J      26            , ^{( )}

∂ f            knV k ′ n ′ k ′ n ′ V kn ± 1

kn ρ kn ± 1 = π ieE ∑     ( y_k ′ - y_k )                      (δ(ε _n ′ -ε _n )+δ(ε _n ′ -ε _{n ±1} )) .        (12)

∂ε                  ε - ε n k n                                n±1 n

где μ – химический потенциал, θ – температура электронного газа. При ц >> 0 интеграл, входящий в выражение (19), приближенно равен:

После подстановки (12) в (6) и ряда преобразований получаем следующее выражение для поперечной магнитопроводимости графена:

”     /22                   пiюHЕ2       л_ 2 2 3 2 / 2 2 А ( л_ 2      2 А пiк ^aH f= 2 F \H^.c I ch-2 Гс^н! e .2. F dE . 2n ^ aH FI OHL |sh-i| 2ПА?Нан Ie >'ui 0    (2h2uF)    ( 26 )                h2oF (2h2uF J ( h2uF )

σ yy =-^{π e 2} ∑∑ A n ^{∂ f} ( y k ′ - y k ) ² k ′ n ′ Vkn ² δ ( ε n ′ -ε n ) .        (13)

h nk n ′ k ′ ∂ε n

Подставляя (20) в (19), получаем следующее выражение для магнитопроводимости графена:

Множитель A , входящий в формулу (6), имеет вид               ⁿ

° yy

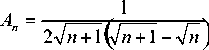
G_n _| ц ² )L      4 п ² кц .if 4 п ² кц)   Г 2 пкц ²

—Л F I      I I 1 +            sh || cos | —

F (9 ² q J( K=t 9 q ( 9 q J ( 9 ² q

Пусть электроны в графене рассеиваются на акустических фононах. Тогда потенциал рассеяния можно

где q = 2h ² u F /0 ² a H , O 0 = e ²Л ² p²/32V2nh ³ p v Ou F •

Выражение (18), как уже говорилось, справедливо, если амплитуда осцилляций мала по сравнению с неосциллирующей частью. Как видно из (21), для этого необходимо, чтобы аргумент функции sh x был достаточно большим по сравнению с единицей. Это приводит к следующему условию, ограничивающему величину напряженности магнитного поля:

H <