Осесимметричная задача об опорном давлении на деформируемый угольный пласт

При аналитических исследованиях напряженно-деформируемого состояния массива горных пород в окрестности подземных выработок используются, как правило, методы механики сплошной среды, в частности, теории упругости. При этом массив моделируется упругой средой с начальным напряженным состоянием, обусловленным весом и боковым сжатием пород.

Рассмотрим угольный пласт, залегающий на глубине H от дневной поверхности. Обозначим его мощность через 2 h . Пусть в пласте проведена вертикальная цилиндрическая выработка кругового сечения, радиус которого равен a . Введем цилиндрическую систему координат л 5^ , совместив плоскость z = О с контактной поверхностью угольного пласта и вмещающих пород. Начало системы координат расположим в центре круга, являющегося потолком выработки (рис. 1).

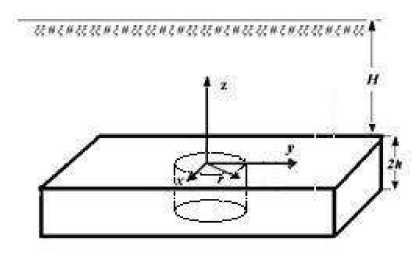
Рис. 1. Схема угольного пласта с цилиндрической выработкой.

В цилиндрической системе координат исходные напряжения ненарушенного массива записываются следующим образом:

а r ⁰ = о ⁰ = а g ( H  z ),   а z ⁰ = р g ( H  z ),   Т r ⁰ 9 =^ z ⁰ ₉=Т_y ⁰ _z  0 .              (1)

Здесь а 0 _, ст ⁰ ,..., т ⁰ – компоненты тензора нормальных и касательных напряжений, <7 – коэффициент бокового распора, ρ – средняя плотность горных пород, g – ускорение силы тяжести.

При наличии выработки полные напряжения в массиве могут быть представлены в виде суммы исходных и дополнительных напряжений

^T ^Г + ^r> ^e ^6 + ^9j ""J ^rz ^rz "+" ^rz

В случае достаточно большой глубины залегания пласта влиянием дневной поверхности на дополнительные компоненты напряжений, появление которых связано с созданием выработки в массиве, можно пренебречь. Тогда задача о напряженно-деформированном состоянии массива горных пород может быть сведена к смешанной задаче теории упругости для полупространства, лежащего на перфорированном упругом угольном пласте.

Сформулируем граничные условия смешанной задачи для упругого полупространства , моделирующего массив горных пород, расположенный над угольным пластом. С учетом формул (1), (2) имеем:

;

;                                (3)

.

Здесь          – вертикальные смещения точек контактной поверхности пород с угольным пластом, – коэффициент постели винклеровского основания, который прямо пропорционален модулю Юнга угольного пласта и обратно пропорционален его мощности.

Приложенная в круговой области распределенная нагрузка постоянна, поэтому смешанная задача (3) для упругого полупространства осесимметрична. Следовательно, компоненты напряжений и перемещений не зависят от угловой координаты , что учтено при записи граничных условий (3).

В    случае    осесимметричной    деформации    изотропного полупространства      компоненты дополнительных напряжений определяются из уравнений равновесия[1]

r         rz       r rz  r

6т 6(T Trz _

--rz +--z +_rz _Q r  zr

и закона Гука

6_r= ^[<7 _r- V{a_e z-]y_z )]

E

^ee= ^^[<7y-v(<7 _r*CT_z ^)]

E

⁶z = ^[^ z - ^r + ^Л

V =-- T rz          rz

^G 1

В формулах (5) компоненты тензора деформации связаны с перемещениями            соотношениями Коши u   u   w   uw

£_r^— ~ ^sSq ^{— —} ^S_z^—     ’%,-7^— "5 l" ,

r r        r   z z    rz z r и удовлетворяют условиям совместности деформаций Сен-Венана[2].

Решение системы уравнений (4)-(6) при граничных условиях (3) приведено в работе [3], в которой с помощью интегрального преобразования Ханкеля [4] получены аналитические формулы для компонент тензора напряжений и вектора перемещения в точках упругого полупространства и на его границе.

В работе [5] решение преобразовано путем перехода от трансформанты к оригиналу введенной вспомогательной функции, характеризующей плотность нагрузки в круговой области, построено интегральное уравнение для ее определения, получена формула для нормального напряжения    на границе полупространства. Учитывая результаты работы [5], формулу для расчета опорного давления на угольный пласт запишем в виде

,(7)

где

2k 1    2 ,

E v , Е – коэффициент Пуассона и модуль упругости пород.

Функция        задается равенством

Здесь  - функция Бесселя первого рода нулевого порядка[6].

Функция     определяется из решения интегрального уравнения

Результаты численных исследований опорного давления на угольный пласт в окрестности цилиндрической выработки приведены на рис. 2 – 4.

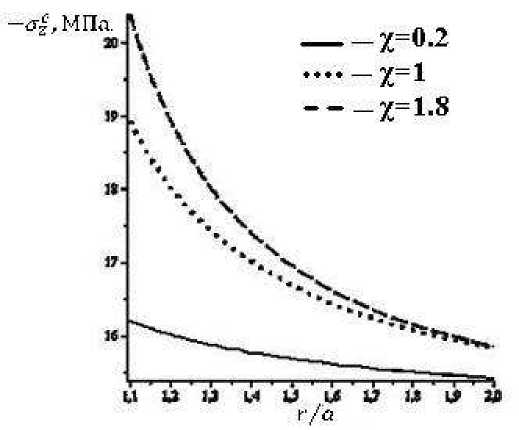
Рис. 2. Распределение опорного давления на угольный пласт при Н =600м.

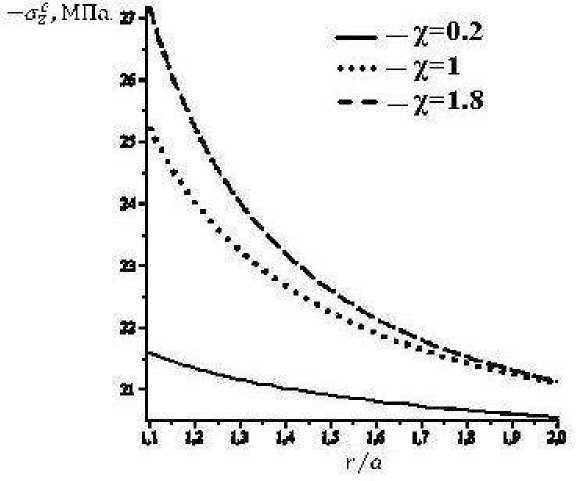
Рис. 3. Распределение опорного давления на угольный пласт при Н =800м.

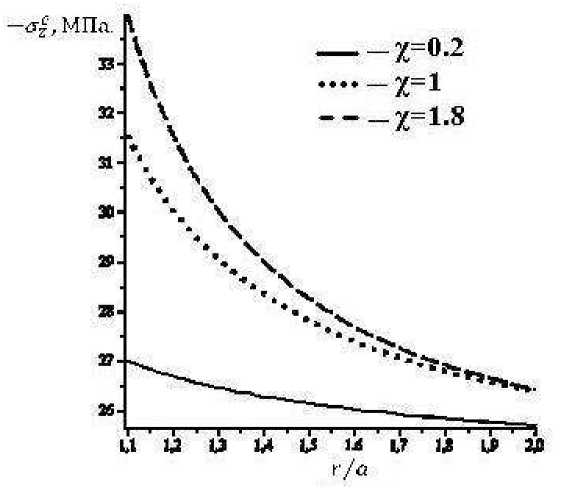
Рис. 4. Распределение опорного давления на угольный пласт при Н =1000м.

Полные нормальные напряжения на контакте угля с породами рассчитывались по формуле у/С^, 0) = -pgHXaz, при этом дополнительное напряжение Oz определялось из соотношений (7),(9),(10). Графики на рис. 2-4 позволяют установить влияние глубины H и параметра Z, характеризующего деформируемость угольного пласта, на распределение опорного давления ^z .

Расчеты опорного давления выполнены для значений параметра z, равных 0.2;1;1.8 M ¹ , при изменении безразмерной радиальной координаты т/ a от 1.1 до 2. Из графиков следует, что максимум опорного давления достигается при т/а = 1 (цилиндрический забой угольного пласта). С ростом параметра X от 0.2 до 1.8 максимум увеличивается. При удалении от выработки, когда т/а> 1, кривые монотонно убывают, приближаясь к значению горного давления yH . Из графиков видно, что при меньших значениях параметра X убывание происходит медленнее. Поэтому при дальнейшем увеличении радиальной координаты, когда r/a > 2 , кривые могут пересекаться, а закономерности зависимости опорного давления от параметра X изменяться.

Количественную оценку влияния глубины H на распределение опорного давления можно получить из сравнения кривых на рисунках 2-4, соответствующих одинаковым значениям параметра X . Так, рисунки 2,4 показывают, что при изменении H от 600 м до 1000 м максимум опорного давления увеличивается при Z = 0.2м ¹ на 56%, приZ= 1-8m ¹ на 67%.

Из графиков видно также, что при фиксированном значении zс ростом глубины опорное давление вблизи выработки увеличивается. Этот вывод подтверждает общеизвестную закономерность.

В заключение отметим, что численные результаты для дополнительных напряжений G_z при z — i , полученные предложенным выше методом, практически совпадают с графическими данными, приведенными в работе [7].