Осесимметричные течения с прямой звуковой линией

В связи с задачей профилирования сверхзвуковых частей плоских и осесимметричных сопел, а также оптимальных контуров сопел ракетных двигателей, реализующих максимум тяги, прямой звуковой линией занимались многие знаменитые ученые. Первыми серьезный вклад в исследование течений с обеих сторон от нее внесли К. Гудерлей [1] и Л. В. Овсянников [2], но течения с прямой звуковой линией не были рассмотрены полностью. Важное свойство таких течений - возможность раздельного рассмотрения и расчета течений в дозвуковой и сверхзвуковой частях. Это свойство и использовалось в задачах оптимального профилирования. Построение оптимальных контуров осуществляется методом характеристик, современная реализация которого изложена, в [3]. Однако отход от прямой звуковой линии в рамках метода характеристик невозможен, поэтому Ю. Д. Шмыглевский с коллегами развил подходы, описанные, например, в [4], позволяющие строить начальную характеристику требуемого семейства. В связи с задачами оптимального профилирования, описанными в [5, 6] возник интерес к сверхзвуковым течениям, ограниченным звуковой линией тока, поэтому в [7] кроме течений, рассмотренных ранее, изучались и такие течения.

Далее осесимметричные течения с прямой звуковой линией изучаются в рамках единого подхода, который опирается на. справедливые в рассматриваемой области универсальные уравнения околозвукового приближения и на. численное интегрирование полученных обыкновенных дифференциальных уравнений. Затем строится начальная характеристика, пересчитывается на. конкретный газ и начинается расчет методом характеристик. Данное исследование носит уточняющий характер, но в нем есть и несколько новых моментов, касающихся сверхзвуковых осесимметричных течений, одна из границ которых - звуковая линия тока.

2.    Исходные уравнения для осесимметричных течений и уравнения околозвукового приближения

Для реализации прямой звуковой линии набегающий поток должен быть однородным по энтропии и полной энтальпии, также в нем должна отсутствовать закрутка. Течение далее стационарно, а газ идеальный, вектор скорости V и скорость звука а отнесены к критической. Ось ж направлена по потоку нормально к прямой звуковой линии. Пусть (1 + и) - ж-компонента V, а ж - его компонента, нормальная к оси ж, на прямой звуковой линии и = ж = 0. Неизвестные и и ж удовлетворяют двум уравнениям: следствию уравнения неразрывности в околозвуковом приближении и условию безвихренности:

2 ди   дж ж    q ди

-

дж

= о. дж

дж   дг   г    ’ дг

Множитель о2 равен о2 = у + 1. и после пре образования го = го2/3,ио = ио2/3 получаются уравнения в околозвуковой форме, одинаковой для газов с разными термодинамическими свойствами:

дио   дж ж ^ дио о дж дго го     , дго

-

дж дж

= 0.

С ±-характеристики в плоскости жг_о определяются уравнениями

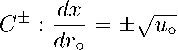
Как ранее было показано в [1, 2, 4, 7], наиболее интересны решения вида ио = ж2U(го),ж = ж3У(го), использование же V как модуля скорости оговаривается далее отдельно при необходимости. Подстановка этих решений в (1) дает обыкновенные диффе ренциальные уравнения:

dV + V dго го

= 2U ² , ^d ^ = 3V dг о

и их следствия

dV ^о   2U^о2г^о - V^о dг^о     1

dU ^о      3V^ог^о ’ dU ^о 3V^о’

где новые переменные ж^о,г^о,U^о, V^о — это нормированнные на постоянную интегрирования старые. В зависимости от значения постоянной интегрирования изменяется диапазон значений U ^о.

Решения симметричны: и(—ж,г) = и(ж, г), ж(—ж, г) = —ж(ж,г), и это справедливо не только в околозвуковом приближении, но и для решений, описывающих осесимметричные течения полных уравнений Эйлера в силу их инвариантности относительно изменения знаков координаты ж и компоненты ж скорости газа. Поэтому все приведенные решения справедливы с обеих сторон от прямой звуковой линии. При отрицательных ж тормозится сверхзвуковой поток в сужающемся канале слева от прямой звуковой линии. Наоборот, при положительных ж тормозится дозвуковой поток и разгоняется сверхзвуковой. Так значе ния U^о >  0 отвечают сверхзвуковому ■течению, а. отрицательным — 1 6 U^о< 0 отвечает дозвуковое течение, ограниченное сверху и снизу кривыми звуковыми линиями, которые подходят по нормали к прямой звуковой линии. При U^о ю ю получаются центрированные волны разрежения или сжатия в концевых точках отрезков прямых звуковых линий.

Для расчета методом характеристик примыкающих к прямой звуковой линии сверхзвуковых течений необходима начальная С±-характеристика, и для ее определения получим уравнение и проинтегрируем его:

dжо жо dU° = ± 2U°’ а затем вернемся к изначальным переменным. В переменных ж, г, и и ж используем начальную характеристику для определения по конечным формулам прочих параметров потока и дальнейшего счета методом характеристик.

Значению U ^о = го отвечает фокус центрированной волны, и для расчета параметров вблизи нее привлекаются асимптотические формулы. Точка фокуса для двух различных видов течения обозначается через г^д.

Функции г О ( U^о) и гО ( U^о) с асимптотами г02 = г^ 1 2, найденные для положительных и отрицательных значений константы интегрирования, представлены на рис. 1 кривыми и горизонтальными отрезками, помеченными цифрами 1 и 2. Горизонтальные отрезки -значения, рассчитанные по асимптотическим формулам. Тот же смысл имеют сплошные и штриховые кривые УД = уо(U^о) на рис. 2.

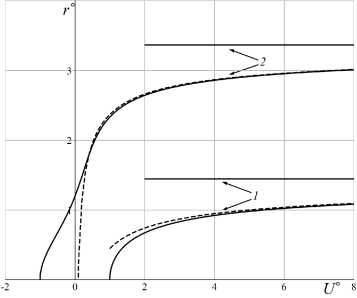
Рис. 1. Функции г°(U °) и г° (U°) с асимптотами Рис. 2. Функции У1°(U°) и У₂^О(U°) с асимптотами

В дополнение к простым осесимметричным течениям были рассмотрены течения в кольцевых каналах с центральным телом. Центральное тело может быть цилиндрическим, сужающимся и расширяющимся с горизонтальной касательной при ж = 0. Внешний контур канала может быть цилиндрическим, расширяющимся и сужающимся. Как и ранее, возможны «отражения» (с изменением знаков жиж) перечисленных вариантов. Используя различные граничные условия для центрального тела в зависимости от его типа, интегрируются уравнения осесимметричного течения. Значению U^о = го, как и ранее, отвечает центрированная волна. Найденные в результате U ^о (г^о) и У ^о (г^о) позволяют построить начальные С +- и С --характеристики для дальнейшего продолжения расчета сверхзвукового течения методом характеристик.

3.    Течения с прямой звуковой линией и нормальными к ней звуковыми линиями тока

Переход к осесимметричным звуковым линиям тока, уходящим с прямой звуковой линии (приходящие получаются изменением знаков жиж), начнем с го > 0 — точки прямой звуковой линии, из которой выходит такая линия тока. Построение звуковой линии тока сверхзвукового течения нормальной прямой звуковой линии идет с помощью уравнений (2). Численное решение задачи начинается с задания го и ведется до U ^о >> 1. Далее при известной начальной С --характеристике следует расчет методом характеристик для совершенного газа при критической плотности р* и р*а* взятых за масштабы плотности и давления, р* = 1/у.

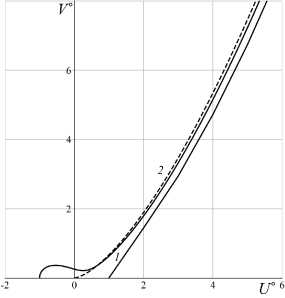
Результаты расчета течений со звуковыми центральными телами, построенными для разных го , приведены на рис. 3. Кривые 1-4 на рис. 3 — контуры звуковых ЦТ для го = 10“³, 10“², 0.1 и 0.5 в координатах ж = ж^о /г^,г = г ^о /г^. В масштабе рис. 3 кривые 1 и 2 совпадают.

Для центрального тела 4 вместе с его контуром приведена многократно разреженная сетка С -характеристик. Во всех рассчитанных примерах С ^характеристики с удалением от прямой звуковой линии пересекаются.

Совпадение построенных для го = 10“³ и 10“² кривых 1 и 2 на рис. 3 позволяет рассчитывать на их близость к контуру звукового центрального тела, начинающегося на оси ж.

Рис. 3. Звуковые центральыне тела различных радиусов

И действительно, удалось построить остроконечное (с Tq = 0) звуковое центральное тело. Контур звукового центрального тела и многократно разреженная сетка характеристик даны на рис. 4а. Программа для метода характеристик не строит висячих скачков, возникающих из-за пересечения одноименных характеристик, однако сам факт пересечений устанавливается достоверно. Также интересно расщепление висячего скачка. Более полную информацию о течении в построенном осесимметричном канале дает численное интегрирование полных уравнений Эйлера на адаптированной к особенностям течения сетке со сквозным счетом разрывов. Результаты такого расчета представлены на рис. 46.

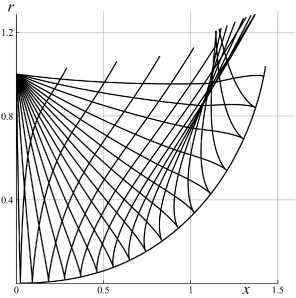
а)

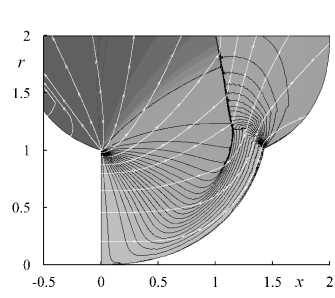
б)

Рис. 4. Звуковое центральное тело, начинающееся на оси

4.    Заключение

Результаты выполненного исследования наиболее полные из всех, полученных ранее. Вдобавок построены примыкающие к прямой звуковой линии сверхзвуковые течения, одна из границ которых - звуковая линия тока. Из них особенно интересно реализующееся обтекание остроконечного звукового центрального тела, начинающегося на оси симметрии.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (код проекта 17-01-00126).