Осесимметричные винтовые течения идеальной жидкости

«Основным допущением, сыгравшим историческую роль в деле приближения теоретической гидродинамики к конкретным приложениям, явилось предположение об отсутствии в движущейся идеальной жидкости завихренности» [1]. Теоретическим обоснованием этого предположения служит теорема Кельвина о сохранении циркуляции [1, 2, 3]. Из этой теоремы следует, что безвихревые жидкие объемы во время движения идеальной несжимаемой жидкости остаются безвихревыми. То есть если в набегающем потоке завихренность отсутствует, то ее нет во всем течении.

Для стационарных течений кроме завихренности есть еще один вектор, который, будучи равен нулю в некотором жидком объеме, во все время движения этого жидкого объема продолжает оставаться нулевым вектором. Это – векторное произведение завихренности на скорость: rotV х V . Если этот вектор равен нулю в некотором жидком объеме, то вихревые линии (для стационарного течения) совпадают с траекториями частиц жидкости. Последние, в свою очередь, согласно теоремам Гельмгольца [1, 2, 3], во все время движения этого жидкого объема будут составлять вихревую линию, и поэтому она останется лежать на траектории. Следовательно, вектор rotV х V останется равным нулю. То есть если в набегающем потоке стационарного течения завихренность параллельна скорости ( rotV х V = 0), то она будет параллельна скорости во всем течении. Поэтому в рамках модели идеальной несжимаемой жидкости изучение стационарных винтовых течений, то есть течений, в которых rotV х V = 0, также содержательно, как и изучение безвихревых течений.

Громека в работе [4] рассмотрел частный случай стационарных осесимметричных винтовых течений, а именно течений, в которых Q = rotV = A V = 0, где А = const. Решения

Громеки представляют собой разнообразные и интересные решения, которые могут использоваться, например, при верификации численных алгоритмов. В исследованном Арнольдом так называемом ABC-течении [5] коэффициент А равен единице, то есть, как и в решениях Громеки, А = const. При этом примеры точных решений с переменным по пространству коэффициентом А, по всей видимости, отсутствуют. Во всяком случае, для осесимметричных течений в доступной авторам литературе не удалось найти ни одного такого решения. В частности, упоминание о таких решениях отсутствует и в классических учебниках [1–3], и в монографиях [6–7], и в обзоре [8]. Нет таких решений и среди самых современных результатов [9–12].

В данной статье получены точные решения уравнений Эйлера для осесимметричных винтовых течений с переменным по пространству коэффициентом А.

2.    Уравнения движения

Рассмотрим осесимметричное стационарное течение идеальной несжимаемой жидкости в потенциальном поле массовых сил. Будем использовать безразмерные переменные: V – скорость; Q = rotV - завихренность; р - давление, отнесенное к плотности; П - потенциал объемных сил. Движение жидкости описывается уравнениями Эйлера, которые можно представить в форме Громеки–Ламба [1, 3]:

Q х V = -V [р + V 2 + п| ,

div V = 0.

Введем цилиндрическую систему координат г, р, z с началом в точке О так, чтобы ось Oz совпала с осью симметрии течения. Параметры осесимметричного течения не зависят от окружной координаты р. Пусть e _r , е , , e _z - правая тройка единичных векторов в радиальном, окружном и осевом направлениях соответственно. Вектор скорости закрученного течения имеет вид V = V _r e _r + V ^ e , + V _z e _z , а функции V _r , V , , V , , р и П зависят только от г и z. Поэтому правая часть (1) имеет нулевую окружную составляющую.

3.    Уравнение винтового осесимметричного течения

Функция тока любого стационарного осесимметричного течения подчиняется уравнению Майзеля, впервые полученному в [13]. Вывод этого уравнения можно найти в [4, 13] и в учебнике [2, гл. 7]. При условии, что rot V х V = 0, уравнение Майзеля и его вывод становятся проще. Получим это уравнение непосредственно для случая rot V х V = 0.

В цилиндрических координатах, с учетом независимости параметров течения от окружной координаты р, уравнение неразрывности (2) записывается в виде: Г-і? (rV _r ) + d, V _z = 0. Отсюда следует существование функции тока ф = Ф ( г, z) такой, что

V r = 1 -^ф,    V , = -¹ -^ф.                         (3)

r dz           r or

Обозначим g = rV, (т.е. V, = g/r).                                   (4)

Вычислим завихренность поля скорости в цилиндрических координатах:

^Q = ( ^— d?^ ) e ^{r +} ( 1b ^{V r —} 11r ^{V z} ) e , ⁺ ( rib ^(rV , ⁾) e ? =

= ^{( —} 1 H g ) er ⁺ ( Ш^{ф +} И ⁽ ГІГ ^ф))^e , ^{+ (} rb g ) e , или, обозначая для сокращения записи:   Q ,     =     1 ЦлФ + Иг ( 1 1?^) ,

Q = (— 1 g? g) e _r + Q , е , + (1¹ 1? g e _z . Поэтому векторное произведение Q х V можно записать в виде

Q x V = - ( Q .1 £ * + £ g & g) e +

+ . 2 (( d. g ) ( dl * ) - (£ * ) ( dl g )) e . -

- (Q . ¹ ^* + g^g) e i .                           (5)

\ r oz    r ² oz )

В винтовом течении Q x V = 0. Поэтому множитель при векторе e . в правой части (5) равен нулю. То есть (g. g) (g|*) - (g; *) (g| g) = 0 или V g x V * = 0. Согласно (3), нулевой градиент функции тока * соответствует нулевой радиально-осевой скорости V = V . e _; + V_z e _z , то есть соответствует случаю V . = V _z = 0. Таким образом, всюду, кроме областей с нулевой радиально-осевой скоростью, из условия Vg x V * = 0 с необходимостью следует, что g = g⁽*Y

Дальнейшее исследование проведем для областей, в которых нет открытых зон с нулевой радиально-осевой скоростью. Обозначим g ' = g'(*) = g^ g и представим (5) в виде

Q x V = - k " + ⁷ gg') (£*) e . + 0 - e .

-

(^Q . 1 ^{+ 7} «') (dz*) ^e «

-

f Q . 1 + ⁷ ggj v *

Поскольку радиально-осевая скорость не равна нулю, то V * = 0. Поэтому из равенства Q x V = 0 следует, что

(^Q. _r + ⁷ gg') = ⁰ ,

или

1£ * + » (1 »*\ + 1 gg = 0, r oz2    dr yr dr / r где g = g(*)- (8)

С другой стороны, если * = *(r, z) — решение уравнения (7) для какой-либо функции g = g(*), то для произвольного потенциала П = П (r, z) решением уравнений (1), (2) будут функции V., V., Vz, определяемые равенствами (3), (4), и давление р = ро — 0.5 (V.2 + V.2 + Vz2) — П, (9)

где р о - любая константа, обеспечивающая положительность выражения (9).

Окончательный вывод состоит в том, что для областей, в которых нет открытых зон с нулевой радиально-осевой скоростью, могут существовать такие и только такие осесимметричные винтовые течения идеальной несжимаемой жидкости, в которых выполнено уравнение (7) при условии (8). Уравнение (7) является основным уравнением осесимметричного винтового движения.

Уравнение (7) при g = 0 соответствует незакрученным (V . = 0) течениям. Незакрученное течение не может быть винтовым (поскольку его завихренность перпендикулярна скорости), и здесь рассматриваться не будет.

4.    Решения Громеки и уравнение для винтового течения с переменным отношением завихренности к скорости

Для винтовых течений коэффициент А, связывающий завихренность и скорость ( Q = A V = 0), может быть рассчитан как отношение окружной составляющей завихренности к окружной скорости: А = Q . /V . . Учитывая (4) и (6), имеем:

A = Q p/V = rQ р/д = — д'. Громека в работе [4] исследовал течения с постоянным полем Л и из условия A = —д' = const = — к получил вид функции д: д = кф. В итоге все семейство решений Громеки может быть кратко описано следующим образом. Это поля скорости и давления, которые вычисляются по формулам (3), (4) и (9) из различных решений уравнения

I (- N + ^ (1 Я + к 2 ф =0, dr yr dr / dz у r dz / r

полученных методом разделения переменных.

Поскольку A = — д ' , с помощью уравнения (7) можно получить точное решение с переменным полем Л, только если функция д = д(ф) будет нелинейной. В общем случае для нелинейной функции д = д(ф) уравнение (7) становится очень сложным, и трудно получить какое-нибудь его точное решение. На эту сложность указывал еще Бэтчелор в учебнике [2, гл. 7] и ограничивался рассмотрением линейной функции д = д(ф). Однако в данной работе удалось подобрать нелинейную функцию д = д(ф) так, что к получившемуся уравнению (7 ) стало возмо жным применить метод разделения переменных. Это - функция д(ф) = V С + 2аф + фф ² , где а и ф - произвольные константы, а константа С обеспечивает положительность подкоренного выражения, что всегда возможно для ограниченных областей, занятых течением. Если а ² + ф ² = 0, то можно так подобрать константу С , что функция д станет нелинейной. Новизна данной работы основана на использовании этой функции. Несложно проверить, что дд' = а + фф, и уравнение (7) принимает вид, допускающий применение метода разделения переменных:

ф Ф фф) + ф Ф фф) +« 1+фф =0, or \r dr j dz \r dz / r r

где а и ф - произвольные константы, а ² + ф ² = 0. Различные решения этого двухпараметрического (а и ф) семейства уравнений будут давать примеры точных решений винтовых течений с переменным полем Л.

В частном случае а = 0 и ф > 0 уравнение (11) превращается в уравнение Громеки (10). Решения этих уравнений совпадают. Поэтому совпадают поля радиальных и осевых скоростей решений Громеки и решений, предложенных в данной работе. Но поля окружных скоростей и, как следствие формулы (9), поля давлений будут различны. Действительно,

Громека рассчитывал окружную скорость по формуле Vp = кф/r и получал постоянное поле Л = —к. А согласно предложенному в данной работе подходу окружная скорость при

V C + фф ² Jr. В

а = 0 рассчитывается по формуле Vp = результате получается переменное

поле Л.

Однако при ф <  0 уравнение (11) не сводится к уравнению Громеки ни при каком значении а. Поэтому в полученных ниже решениях для ф <  0 не только окружная скорость, но и все остальные компоненты скорости не совпадают со скоростями, полученными Громекой.

Заметим, что величина Л в полученных ниже решениях различна на линиях тока, у которых не совпадают поверхности вращения этих линий вокруг оси симметрии. При этом на любой линии тока величина Л сохраняет свое значение. Это не говорит об узости класса найденных решений. Нет смысла искать решение, в котором поле Л меняется вдоль линии тока. Дело в том, что из условия Q = Л V = 0 с необходимостью следует, что величина Л сохраняется вдоль линии тока [4].

5.    Примеры точных решений

Если течение происходит в зазоре между двумя соосными поверхностями вращения, то такое течение не содержит ось симметрии. Поэтому представляется содержательным учет не только тех решений уравнения (11), которые не имеют особенности на оси симметрии, но и учет решений, имеющих такую особенность. Для представления точных решений уравнения (11) удобно отдельно рассмотреть три случая: ф = 0, ф = —к2, ф = к2, где к = 0 - произвольная константа. В каждом из этих случаев метод разделения переменных приводит к разным результатам. Опуская выкладки, приведем соответствующие точные решения.

• 5.1.    Случай 3 = 0

Решением уравнений Эйлера являются функции:

V = - тг"3,   V- = -- "1"^, V = V С + 2а3 /г г dZ             г дг                     /

и р = ро - 0.5 (^2 + ^2 + У2) - п, где константа а может быть выбрана произвольно. А константа С выбирается после выбора функции тока 3 и должна обеспечивать положительность подкоренного выражения в рассматриваемой области течения. Функция тока 3 может быть выбрана как 3 = 3 — (аг2 lnг)/2, где 3 является произвольной линейной комбинацией функций вида:

гJ1(p1г) exp(p1 z), rJi(pir) exp(-рі z),(12)

гУ1(р2г) exp(p2z), гҮі(р2г) exp(-p2z),(13)

гІі(рзг) sin(p3z), гI1(pзг) cos(p3z),(14)

гK1(p4г) sin(p4z), гКі(р4г) cos(p4z),(15)

г2, zг2, z,(16)

где p 1 , p 2 , p 3 , p 4 - произвольные положительные константы; J i , Ү і - функции Бесселя и Неймана первого порядка; І і и К - цилиндрические функции мнимого аргумента первого порядка [14, гл. VII].

• 5.2.    Случай 3 = - к², к = 0

Для каждого фиксированного набора чисел а и к = 0 решением уравнений Эйлера являются функции:

1 д ~

V _r = -^3, V , г dz

— —3, V _v = ^С + 2а ( 3 - а / к ² ^ - к ² ( 3 - а / к ² )    г

и р = р0 - 0.5 (У2 + Vip2 + У2) - П, где константа С обеспечивает положительность подкоренного выражения в рассматриваемой области течения и выбирается после выбора функции 3- В качестве функции 3 можно взять произвольную линейную комбинацию функций вида

гJ1(p1г) exp(m1 z), гҮі(ріг) exp(mi z), ті = к2 + рі; (17) гІі(р2г) exp(m2 z), гКі(р2г) exp(m2 z), m2 = к2 - - P2; (18) гІі(рзг) sin(m3 z), гІі(рзг) cos(m3 z), m3 = P3 - - к2; (19) гКі(р4г) sin(m4 z), гКі(р4г) cos(m4 z), ™2   2 m4 = p4 - - к2; (20) гzІ1 (|к| г); гz Кі(|к| г); exp(кz); г2 exp(кz); (21) где рі - произвольная положительная константа, а константы р2,рз,Р4 положительны и выбраны так, что р2 6 к2, р2 > к2 и р4 > к2.

• 5.3.    Случай /3 = к², к = 0

Для каждого фиксированного набора чисел а и к = 0 решением уравнений Эйлера являются функции, вычисленные по формулам:

V = 1 д^’ V z = - г dr^’ ^ = VС + 2а ( ^ - а / к ² ) + к ² ( /> - а / к ² )    г

и р = ро - 0.5 (VT2 + Vp2 + Y2) - П’ где константа С обеспечивает положительность подкоренного выражения в рассматриваемой области течения и выбирается после выбора функции ^. В качестве функции ^ можно взять произвольную линейную комбинацию функций вида:

гІ1(р1г) sin(m1 г),    гІ1(р1г) cos(m1 г),    m2 = к2 + рі;(22)

тК1(р2г) sin(m2г), тК1(р2г) cos(m2г), m2 = к2 + р2;(23)

rJ1 (рзг) sin(m3г),   гJ1(pзr) cos(m3г),   m2 = к2 - р2;(24)

гУ1 (р4г) sin(m4г),  гУ1(р4г) cos(m4г),    m2 = к2 -р4

r 71(р5г) exp(m5 г),  гУ1(р5г) exp(m5 г),    m2 = р5 -к2;(26)

rгJ1(|к| г); ггУ1(|к| г);(27)

sin(кг); сое(кг); г2 sin(кг); г2 со8(кг),(28)

где р і и р 2 — произвольные положительные константы, а константы р з , р ₄ , р 5 положительны и выбраны так, что р ² < к ² , р ² < к ² , р 5 > к ² .

Еще раз заметим, что решения раздела 5.3 при а = 0 можно рассматривать как обобщение решений Громеки на течения с переменным коэффициентом А.

6.    Линейная комбинация решений

В предыдущем разделе отдельно для каждого из случаев 3 = 0, 3 = - к ² и 3 = к ² приведены наборы функций (12) – (16), (17) – (21) и (22) – (28), из которых можно составлять линейные комбинации для получения функции ^. Эти наборы функций позволяют «конструировать» различные точные решения. При составлении линейных комбинаций следует учитывать три обстоятельства.

• 1.    Поскольку в уравнение (11) константа к входит в виде к², в набор (17) - (21) можно включать как функции exp(kг) и г²exp(кг), так и функции exp(-кг) и г²exp(-кг).

• 2.    При фиксированном 3 каждая функция, представленная формулами (12) - (15), (17) – (20) и (22) – (26), представляет бесконечное однопараметрическое семейство линейно независимых функций. Так, например, в силу произвольности выбора положительной константы рі, в набор (12) - (15) можно включать функции:

• 3.    Возможность использования параметров m^ с разными знаками не позволяет получить новые линейно независимые функции из функций (19), (20) и (22) – (25). Однако из функций (17), (18) и (26) получаются новые линейно независимые функции. Так, например, согласно (26), при к = 3 можно выбрать р5 = 5, и в набор (22) - (28) - включить как функцию г J1(5r) exp(4г), так и функцию г Ji(5t) exp(-4г).

7.    Пример линейной комбинации

rJ ₁ (r) exp^), г7 1 (г) exp( - г), tJ ₁ (2 t ) exp(2г), t-J^t ) exp( - тг),...

В качестве примера рассмотрим линейн у ю комбинацию функций (24) и (26) для случая к = 2: — i = г J i (V3r) sin(z) и — 2 = гJ 1 (V5г) exp( - z). Поля радиально-осевых скоростей V i = V_r i e _r + V _z i е _г и V 2 = V _r 2 e _r + V _z 2 e _z для таких функций вычисляются по формулам: V- 1 = ¹ /,' '' . = J i ( V 3г) cos (z), V _z i = - ¹ ^— i = -V 3J 0 ( V 3г) sin(z);

V-2 = - Ji(V5r) exp(-z), VZ2 = -V5Jo(V5г) exp(-z), где Jo — функция Бесселя нулевого порядка. Линии тока радиально-осевых скоростей каждого из этих течений в осевой плоскости показаны на рис. 1.

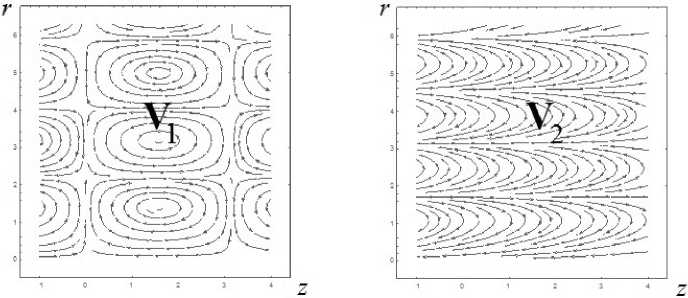
Рис. 1. Линии тока радиально-осевых скоростей в осевой плоскости

Сумма скоростей V = V i + V 2 соответствует функции — = — 1 + — 2 = гJ ₁ (V3г) sin(г) + гJ ₁ (V5г) exp( - z) и является решением уравнений Эйлера. Линии тока суммарного течения изображены в двух разных масштабах на рис. 2.

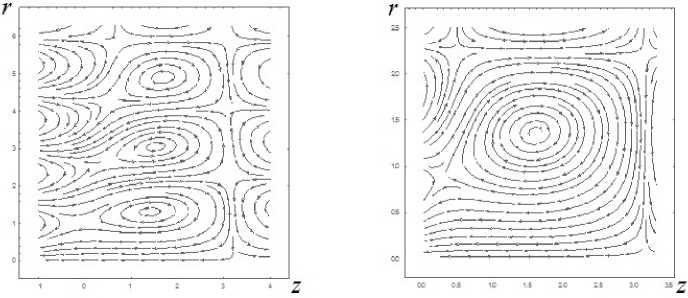
Рис. 2. Линии тока суммарного течения в разных масштабах

Для выбранной функции — радиально-осевая скорость полученного в данной работе течения не отличается от такой же скорости в течении Громеки. Однако окружная скорость будет отличаться. В решении Громеки Vv =2— /г. А в «новом» течении эта ско рость V^

= ^С + 2а ( — - а / к ² ) + к ² ( — - а / к ² ^

г зависит от двух произвольных па

раметров С и а. Единственное ограничение на эти параметры - неотрицательность подко- ренного выражения в рассматриваемой области. Отличие этих скоростей для параметров С = 3, а = 2 хорошо видно на рис. 3, где представлены графики зависимости скоростей

V ^ от радиуса при z = 0.

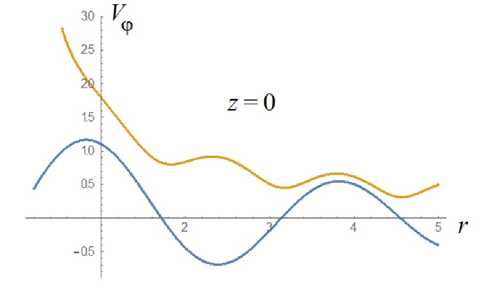
Рис. 3. Графики окружных скоростей при z = 0. Синий цвет - решение Громеки

8.    Заключение

Получены точные стационарные решения уравнений Эйлера для осесимметричных винтовых течений идеальной несжимаемой жидкости. Некоторые из них можно рассматривать как обобщение решений Громеки. В отличие от решений Громеки, в полученных решениях отношение модуля завихренности к модулю скорости не постоянно в поле течения.