Основное математическое тождество в задачах распознавания образов

Рассматриваются многоуровневые иерархические структуры [1] , представляемые как сети со множеством узлов (множеством объектов Ob ) и множеством их связей ( морфизмов H ), т.е. малые категории [2]

% = (Ob,H)

Звено такой сети изображено на рис .1, на котором представлены два состояния: рис. a ) и рис. b ),где aⁱ , bⁱ ϵ Ob , hⁱ j ϵH ; i , j = 0, 1, 2.

Рис.1. К сравнению звена иерархической структуры.

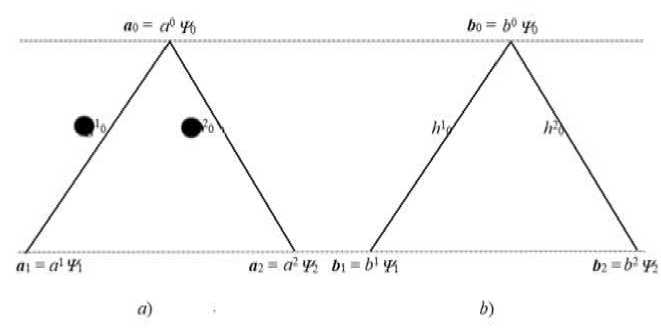
Из рис. 1 видим, что каждый узел сети характеризуется своей собственной функцией ¥ i и отличается только своим собственным значением aⁱ , а состояния a ) и b ) отличаются только амплитудами объектов. Функцию ф определим как волновую функцию [3] соответствующего узла системы в стационарном состоянии [4] .

Амплитуды объектов – числовые характеристики. Будем полагать, что числовыми величинами являются и связи между узлами, т.е. на категории (1)задаётся функтор и каждое состояние определяется своим функтором

А = А(^,= (А(ОЬ\А(Н)),   В = В(К) = (B(Ob),B(H)).(2)

Полагаем, что на данных категориях каждый узел определяется левым модулем , например, для рис. 1 a )

«о = 9111 + д0а2 = g^W + gfa2^(3)

Заданные операции (2) и (3) на множестве узлов сети образуют линейное метрическое пространство (метрический линеал [5, стр. 15] ) с мерой, определяемой внутренним произведением

^аьа^агц,(4)

индуцируемой гомоморфизмом

D(a0 = а? = (a1)2.(5)

Гомоморфизм (5) характеризует скалярную оценку узла. Из соотношений (3) и (5) следует представление результирующей волновой функции в виде

4*0 = aiWi + о^ = шМ, где для пропускной способности соответствующей связи (как доли в формировании единицы амплитуды результирующего свойства), введено обозначение al0 = Wo-4’l= ?£.                        (7)

Собственные функции являются базисом метрического пространства в области сравнения достаточно близких к фиксированному состоянию состояний, которые отличаются только их собственными значениями.

Воспользуемся аддитивной связью между тензорным ab, внутренним и внешним а Л b произведениями векторных величин аЬ = а • Ь + а Л Ь.                           (8)

Произведение (8) можно записать скобкой процедуры Кэли-Диксона, полярной формой аЬ = (а • Ь,а Л Ь) = ^аЬ^и,               (9)

где величина

U = eine

является унитарным кватернионом. Здесь nединичный вектор представления а ЛЬ = | а Л b | n, а аргумент равен

0 = arctg

|алЬ| а-Ь ^.

Заметим, что выражение (8) суть "аксиоматическое изложение евклидовой геометрии" [6, стр. 70] и представляет аддитивное расслоение линеала в евклидову и симплектическую структуры, а свойства гомоморфизма (5) сводит его к теореме Пифагора - к равенству

D(ab) = D(a^ b) + D(aAb), (12) являющееся основным метрическим тождеством [7] материального мира, с мультипликативным представлением

D(ab) = D(a)D(b) (13)

Любая управляемая сеть - сеть прямого распространения [8] . Рассмотрим дихотомическую структуру с одним промежуточным срезом, рис. 2. К таким структурам можно отнести искусственные нейронные сети подобные сетям Хопфилда и Хемминга [9] . Следуя [10] , отметим, что при любом сравнении в той или иной форме всегда присутствует эталон. "Основное назначение эталона состоит в том, что содержащаяся в нём информация определённого типа служит для оценки аналогичной информации в других объектах. … Эталоны могут выбираться или назначаться извне и ни один их них может не принадлежать множеству рассматриваемых объектов".

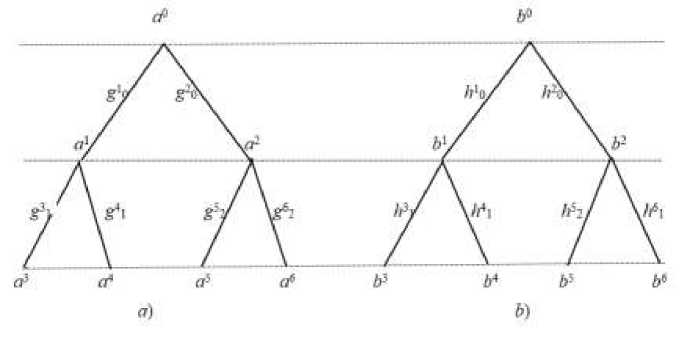
Рис.2. К сравнению дихотомический сетей.

Как видим, бинарное соответствие состояния а некоторого объекта с состоянием выбранного эталона b при анализе удобно представить тензорным произведением ab , при этом полагая состояние эталона нормированным, ||b|| = 1. Вытекающее из такого представления расслоение (8)чётко выявляет две "надлежащие универсальные характеристики фундаментальных структурных элементов материи на каждом данном уровне её самоорганизации", [11 стр. 44] , - качество и количество, где качество характеризуется волновой функцией рассматриваемого элемента данной сети, или её агрегатным значением, а количество определено амплитудой данной волновой функции в той же агрегации.

Не нарушая общности изложения анализа, для упрощения, положим напряжённости связей сети равными единице. Определим в каждом проекционном пространстве координаты результирующих элелентов. Приотображении а, b ^ К2имеем: а = а' = [a 1; a2], b = b' = [b 1; b2]. При a, b ^ R4 имеем: a = a" = [a3; a4; a5; a6], b = b" = [b3; b4; b5; b6]. При этом с промежуточного среза получаем те же оценки что и с нижней границы. Из тождества (12)находим

ab = £6k=3(akbk + ^f=k+1(akbl - albkyPk Л У)

Если рассматривать многослойную сеть с модульной структурой, то видим, что каждый узел формирует подмодуль . Пусть сеть a имеет n =|N| слоёв. Зафиксируем два среза i, jϵN с индикацией узлов подмножествами N i , N j с N . На i- срезе выделим т- узел. Пусть он описывается величиной a _m = a^mΨ m , mϵN i . Предположим, что нормированная сеть (сеть стандартного вида) b , D ( b ) = 1, служит её эталоном. Выражение (14) в общем случае принимает вид