Основное метрическое тождество

Прямой угол в основе строительства и геодезии применялся с древних времён и для его построения использовали построение прямоугольного треугольника, который играл роль геометрической метрической фигуры. Древние египтяне использовали треугольник со сторонами 3:4:5, который греки назвали египетским треугольником. А расшифровка глиняной вавилонской таблички «Плимптон 322», которая служила расчётным планшетом построения прямого угла [1], показало, что свойства зависимости диагонали и сторон прямоугольного треугольника были известны еще задолго до построения пирамид, которые впоследствии в знаменитой теореме были обобщены Пифагором.

Оказалось, что теорема Пифагора показывает не только свойства некоторой геометрической фигуры, но и содержит в себе основные структурные элементы нашего трёхмерного мира в его евклидовости, служит основой построения различных алгебр и, по существу, в современном анализе низведена до аксиоматического изложения определений евклидовой и симплектической структур [2, стр. 70].

Любой объект материального мира выступает «прежде всего в двух (и только в двух!) одинаково существенных и взаимно дополнительных основных характеристиках» [3, стр. 44] – во внешней интегральной количественной и внутренней дифференциальной качественной, что предполагает существование меры.

В геометрической алгебре Клиффорда ℇn [4, 5] индуцированной евклидовым пространством En рассмотрим множество G объектов и определим наложение р: G ^ К = (1,2) так, что для любых объектов f, h и д = fh Е G имеет место расслоение д = gi + g2,                               (1)

где д1 = f • h Е G1,g2 = f Ah Е G2.

Приходим к аддитивному разбиению

G = G 1 + G 2 .                               (2)

Расслоение р, используя гоморфизм D, можно записать в мультипликативной форме, если скалярный квадрат д² = D(g) элемента представить произведением D(g) = д - д⁺, где д - = f • h — f Ah, д⁺ = f • h + f A h, и ввести множества G - Э д - и G⁺ Э д⁺. Получаем

G = G - G + .                             (3)

Здесь внутреннее произведение f • h - скалярная величина которая служит мерой сходства элементов f, h . Действительно, если f → h , то о(д) ^ f • h, а из условия o(f Ah) ^ 0 следует, что f ^ а + ^h, где о = D 1 ².

Из (3) имеем д+ = о(дУ?(ы0) д- = Ф*(ые)о(д),    ^(ше) = exp(^e), в = arctg Р,

где со2 = -1, величина

P = P(f’h~) = ^y v(f,h) = x^^^h).        (5)

Из (4) следует волновое представление [6] элемента (3)

д = У * GW, V * = W(-(De), а применение к (1) гомоморфизма D при обозначениях c² = D(g),a² = D(g 1 ),b² = D(g 2 ), сводит его к тождеству Пифагора - основному метрическому тождеству [7]

c² = a² + b²,                               (7)

которое устанавливает геометрическую связь между свойствами окружности вписанного в неё прямоугольника (рис.1).

Определим математическое ожидание и дисперсию функции f ( x , y ) случайных величин x , y е E n

E(f(x,y)) = ТЛхк'УдРк = хк, у = у,) = Т^р^ХкУ),(8)

^2(f(x,y)) = E((f(x,y) - E(f(x,y))2).(9)

Математическое ожидание примем в качестве метрического отношения между элементами пространства ℇⁿ

g(x,y) = E(f(x,yf), D(x) = g(x,x\(10)

рассматривая E n как некоммутативное кольцо с единицей e е E n , D ( e ) = 1, приходим к основному метрическому тождеству

D(x)D(y) = g2(x,y) + v2(x,y), из которого следует расслоение

D(F(x) = E2(F(x)) + o2(F(x)(12)

функции F ( x ) = f( x , e ) переменной x е E n при фиксации элемента e .

——*

—>

Пусть v = OB , x - случайный вектор и и = ОА. Отражение и относительно горизонтальной и вертикальной осей будет соответственно

1                              1

(и • v)v = -(и + vuv),    (и л v)v = -(и- vuv).

Отсюда находим

и = (ит + ил v)v, и = v(v •u + v Ли),

или

D_v(u) = E_v²(u) + ^_v²(u),                     (14)

^v2(u) = D (и л v).

Равенство (14) по существу совпадает с тождеством (11).

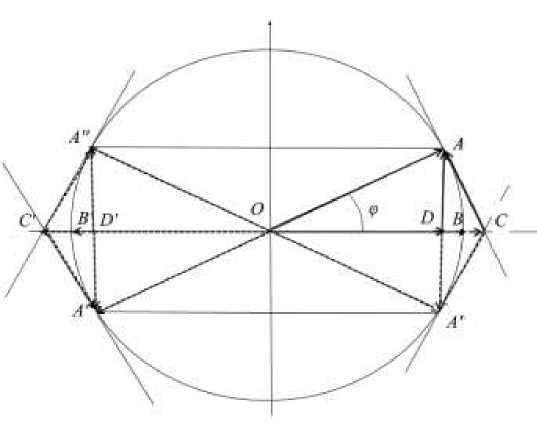
Рис. 1. Геометрическая интерпретация основного метрического тождества.

Положим, что в (11) мера имеет вид

^(х,у) = XieNaiyixi.                       (15)

В пространстве Е^п зафиксируем точку y = (y i : i е N) , выделим некоторую окрестность U_y и сделаем в этой окрестности преобразования координат так, что произвольная точка x е U_y переходит в точку u = x./y = (u i = x i / y i : i е N) , U_y ^ U e , а точка y в точку e = ( e i = 1: i е N) . Данное преобразование преобразует меру (15) в произведение

В(х,у) = Ev2(u) = D(y)E(u),                (16)

где

E(u) = p(u,e) = ) рм,

^—' iEN

P i >0, ^

P i = 1, iEN

равно математическому ожиданию объекта и в окрестности Ue, или объекта x в окрестности Uy. Отсюда же следуют представление

D(u) = E2(u) + (J2(u),

его интерпретация на единичной окружности (рис. 1) и, как следствие, все основные статистические характеристики [8, стр. 28].

Пусть x с ^n числовая последовательность пространства Клиффорда. Обратимся к тождеству (12). Здесь величина |OD| = E(F(x)) будет математическим ожиданием значения функции F(x), IADI = а(F(x)) -среднеквадратическим отклонением данной функции от её математического ожидания, величина |AD|2 = а2(F(x)) - дисперсия. Ранее говорилось, что при измерении всегда присутствует некий эталон, который и соизмеряет разнокачественные объекты. Пусть это вектор ОВ. Величина p = E2( F(x))/D (F(x)) будет равна вероятности математического ожидания значения функции, величина y = D (F(x))/E (F(x)) является средней антигармонической, а величина d2 = |AC|2 = а2(F(x))D(F(x))/E2(F(x)) -степенью точки O относительно данной окружности. Отметим, что метрическое тождество связывает геометрические, алгебраические, статистические и физические величины в диалектическом единстве таких категорий как единичное, особенное и всеобщее, содержание и форма, сходство и различие, качество и количество.