Основное метрическое тождество на бинарных соответствиях в алгебре Клиффорда
Автор: Соловьв А.С.
Журнал: Экономика и социум @ekonomika-socium
Рубрика: Основной раздел
Статья в выпуске: 10 (77), 2020 года.
Бесплатный доступ
Устанавливается связь метрических отношений на основе алгебры Клиффорда с элементами квантовой механики, которые предлагаются для решения проблемы в теории статистических индексов.
Основное метрическое тождество, средние величины, мера, качество, количеств
Короткий адрес: https://sciup.org/140251423
IDR: 140251423
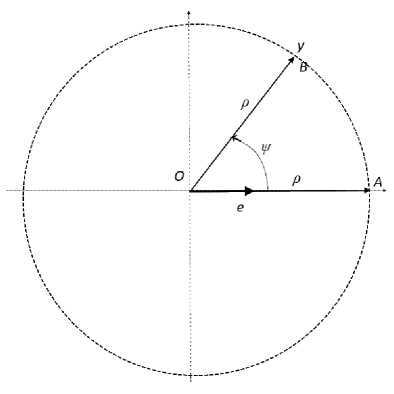
Список литературы Основное метрическое тождество на бинарных соответствиях в алгебре Клиффорда
- Юдин Д.Б. Вычислительные методы теории принятия решений //М., Наука, 1989.
- Ландау Л.Д., Лифшиц Е.М. Квантовая механика, т.3 //М., Наука, 1989.
- Кёвеш П. Теория индексов и практика экономического анализа //М., Финансы и статистика, 1990.
- Ершов Э.Б. Ситуационная теория индексов цен и количеств. М.: РИОР, 2011.
- Иванов Ю.Н. О некоторых базовых положениях теории цен //Вопросы статистики, 2018, Т. 25, №7, с. 23-30.
Статья научная
