Основной метрический треугольник в анализе чувствительности управляемых сетей

Как правило, социальные и экономические системы S имеют иерархическую структуру с внутренней организацией качественного порядка [1] и представляются плоскими орграфами рис. 1. Состоят из объектов Ob =

Рис. 1. Сеть прямого распространения.

{ x 0 , x 1 , x 3 , ...} и связей между ними, морфизмами, а₁₀ = Xi%₀, ^е Мог, т.е. представлены малой категорией

S = (ОЬ,Мог).

На рис.1 представлена схема сети прямого распространения. Такие сети предназначены для создания конечного продукта деятельности. Графы обратной направленности определяются как сети обратного распространения

[2]. В иерархической сети объекты можно представить срезами по критериальным уровням из деятельности. В отличие от [2] назовём слоем орграф между двумя срезами. В зависимости от ориентации графа срезы в таком слое назовём верхней и нижней гранями. Каждый срез у разбивает граф S на два подграфа S и S так, что S = S + U $ - , у = S + A 5 - .

Если система представлена сетью прямого и обратного распространения, то, вероятнее всего, такая система создаёт конечный продукт с внутренним управлением, которое подстраивает её существование к требованиям внешней среды. Такую систему назовём замкнутой. Элемент замкнутой сети изображён на рис. 2.

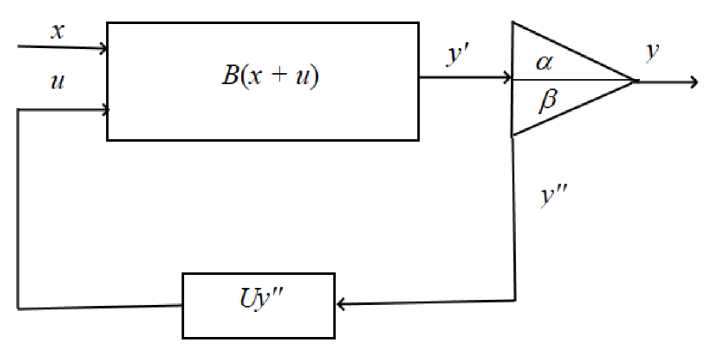
Рис. 2. Схема структурного элемента сети с управлением.

Сеть сама представляет собой управляемый элемент во внешней среде и её представление определённой схемой условно. Схему сети можно агрегировать и дезагрегировать так, что блок сети становиться отдельным её элементом. Представим её категорией в виде объединения элементов и их связей

^ = М   ^т>  $т  (^Ьт, Могт)

'*-' теМ и определим функтор F:5 ^ Я , который отображает описание её состояния в поле вещественных чисел

Я = (Х,ЭД) так, что объекты отображаются на множество векторов Х = F ( Ob ), а морфизмы - на множество прямоугольных матриц ЭД = F ( Mor ). В линейных сетях элементы выполняют роль линейных преобразователей. Но им можно придать и свойства квазилинейности [3].

Из рис. 1 следует, что составляющие элемента x, u, y, y'у'' принадлежат векторным пространствам, а операторы B, U, и а, в — матричным пространствам. Поскольку в общем случае управление отвечает каждому фактору, то если полагать для соответствующего элемента степень захода равной n , а степень исхода равной m , то имеем: x, и с №, у, у', у'' с ^, B с M m x^, Uс ^х^¹, а, в с M m xM m .

Пренебрегая лагом длительности передачи управления и полагая единицу соответствующим тождественным оператором, можно заключить, что схема действия элемента отвечает системе уравнений

г у' = В (х + и),

у'= у+ у".

у = ау', у'' = Ру',

Отсюда находим, что

и = Uy", а + 0 = 1. система работает как сеть прямого распространения, действие которой описывается векторным уравнением у = Ах,                             (1)

с матричным оператором

аВ

А =-------

1 - BU^

где U,^ - матричные операторы, формирующие вектор управления и.

Назовём систему стандартной, если значения на всех её объектах равны единице. К стандартному виду можно привести любую систему вида (1). Если системы имеют одну и ту же структурную схему S (совпадает их графическое изображение, графы) и приведены к стандартному виду, то

T = Af,    у = Вх,  f,т,х,у е X, А,В е 31,

а их действие отличается только операторами A и B . Состояния систем, описание которых приведено к стандартному виду легко сопоставляется. При этом, сопоставляются состояния и любых их подсистем, что удобно при поиске слабых мест при настройке их ориентации поскольку их состояния отвечают только наблюдаемым A и B .

При оценке, сравнении, обучении системы, в задачах поиска всегда предлагается тестовая модель Я 0 состояния системы. Тестовую модель назовём эталоном и представим её в блочном виде

Я о = Н  Я ощ

Jтем

Положим существование её аддитивной меры [4]

• *-^ тем        т-Мем

Текущее состояние Я системы представим в том же блочном виде и определим его меру аналогичным метрическим функционалом

D(V = Я² = У  Я щ2 = У    D_m(&).

• *—> тем      т—МпеМ

На данном расслоении системы определим аддитивную меру поблочного бинарного соответствия W = (Я, Я₀) с метрическим тензором G , который является самосопряжённым оператором

/(W) = У   /(Wm) = У   /m(W),

t—¹ тем       m^M^M

W = H   (W m = (Я m ,Я mo )).

JI meM

Согласованность мер определим равенством

D(Я) = /(Я,Я) = Я * СЯ = Я², Я * = ЯС * , G*G = 1 ^ , и расширим её с диагонального множества на бинарное соответствие состояний, полагая

D(W) = D(Я')D(Я0).

По аналогии с теорией индексов введём индикатор типа Ласпейреса, который определяет меру на множестве W рекурсией

^/(w) = ^ = S_meMp’ " /_m(w),

Ш^Я 0 )

где m.  Dm(Яo)   , „„./WW

Р    D(Яo) '   m( )  Dm(W)

Рекурсия показывает, что любой блок Wm, системы, не являющейся меры нуль, сам является метрическим пространством.

Определим соотношением

D(W)

D^

= 02(W)

индекс полного состава [5, формула (6), стр. 15] и введём дополнительную меру hJ(W) = ±7^2(W)-/2(W), где h > 0 служит множителем пропорциональности. Находим, что три данные меры Ф, I и J на бинарных соответствиях состояний системы связаны основным метрическим тождеством [6]

02(W) = /2(W) + h2J2(W).

При гомотетии [7, стр.57] состояний J ( W ) = 0 и Ф ( W) = I ( W). При структурных различиях (деформации системы [8]) показатель J отличен от нуля. Он монотонно возрастает с ростом структурных сдвигов. При этом, оператор Гамильтона принимает вид

Я = |ф² = T + U, где T = /²(W), U = h²J²(W) операторы фактического состояния системы и её потенциальных возможностей (показатель h можно принять равным единице), трансляции и ротации, соответственно.

Рассмотрим состояние системы (2) и предположим, что на объектах определена с метрическим тензором G вполне аддитивная мера

/(у,т]) =T]*Gy = y*Gr].                           (3)

Определим бинарное соответствие исходов ( y, п ) = w, ему сопряжённое w* = ( П, У ) и введём обозначения:

В = ^(w) = q ⁽ w*\    D(y) = у² = м⁽У,У) = °^{2 (} y\

D(w) = D(y)D(q),  a(w) = a^y^aQq).

Для анализа отклонения исходов приходим к основному метрическому тождеству o-2(w) = q2(w) + |v(w)|2.

Из соотношений (2) и (3) вытекают представления q(y,ri) = ^*A*Gy = rfGBx = %*A*GBx, которое вместе с тождеством (4) позволяют оценивать относительно потоков входа и выхода эталона взаимное влияние фактических потоков.

Определяя состояние объекта величиной a , находим, что на основании

• (4)    состояние можно описать кватернионом

a = q + in]vl = ае1пв,

где n – некоторый единичный вектор¹,

|v|

6 = arctq — В

• - биекция, является показателем вращательной симметрии – показатель оценки структурных сдвигов, и удовлетворяет соотношению Шаля [7, стр. 51].

Если обе части тождества разделить на оценку D ( η ) эталона, то придём к индикаторам теории индексов

D(y)

• • ^ = й(Д) — индекс объёма производства;

^(у,л)

_

• • ^ = ”о(Д)— индекс переменного состава;

\у(ум)\

-

• •    J = о^) --индекс структурных сдвигов.

На основе данных индикаторов определим коэффициент уровня согласованности фактического состояния элемента с эталоном

–

коэффициент корреляции, r = μ/σ . Его квадрат p = d = r ² определяет детерминацию d свойств эталона в состоянии объекта. Его можно рассматривать в качестве вероятности совпадения состояния с эталоном. Квадрат коэффициента вариации к = |v|/o определяет коэффициент остаточной детерминации q = 1 – p = V ², где V = |ν|/σ = tg θ и является показателями структурных сдвигов. Все эти показатели связаны с оценкой состояния системы, с её управлением, обучением, с устойчивостью системы к неожиданным воздействиям. В последнем случае целью обратной связи становится уменьшение системы к изменению её факторов.

Если F = F ( x ) критериальный показатель, то инфинитезимальная характеристика коэффициента чувствительности к изменению xⁱ фактора определяется формулой

dF xl dF

£l   dxl F dx1'

Учитывая представление индекса переменного состава в виде взвешенной суммы индивидуальных индексов

I = Р% имеем:

PiIi £i(n=—, £i(^) =

^(v) = -

p1Ii2 Л2 ’ £i(r)

V2 ,

P^{i I}i^(Ii^- y ⁾             P^{i I}i⁽ y ^-Ii⁾

£i(J) = P ----~p-----, £i(r) =----^----,

£,■ (r)

£i(V) = —^, £i(0) =

-

£i(r) ve ■

В эти выражения входят три средние взвешенные величины: средняя арифметическая I , средняя квадратическая X и средняя гармоническая у, которые связаны равенством Л ² = у1. Поскольку в суммах

У £i(I) = У £i£N(A) = 1

^ ieN i-NieN все слагаемые неотрицательны, то два первых показателя можно рассматривать как вероятности обнаружения соответствующих свойств в оценках арифметической и квадратической средних. Чем больше коэффициент чувствительности, тем больше его влияние на соответствующий показатель. Если для всех носителей свойств i е N имеют место равенства

Ii = Y>

то Л = I = y,J = 0,r = 1 и оцениваемые объекты качественно подобны с коэффициентом подобия равным у.

Из равенств _£i (r) = z_i (I) = z_i (Л) и равенства

У   £ i⁽ f) = 0

^ ieN следует, что носитель N разбивается на два подмножества N+ и N с положительной а+ и отрицательными а чувствительностями коэффициентов корреляции. Из а+ ^ 0 следует r ^ 0. В сумму а+ входят те факторы, увеличение которых приводит к росту качественных отклонений от эталона. Для отрицательных показателей справедливы неравенства

Vi = у - Ii <0,i e N-.

С ростом наименьшего из них будет сокращаться отклонение качества фактического состояния объекта от эталона (уменьшается ротационная составляющая) и будет увеличиваться трансляция. Отсюда заключаем, что задача оптимальных управлений является двухкритериальной - управлением качеством и количеством, которая сводится к игровой задаче [9].

Запишем показатель чувствительности структурного сходства в виде

Z = У-1Р^>

где Pⁱ = £ i (I)u ^i_eNPⁱ = 1, и введём случайную величину V — вектор V = (Vi- i ⁶ Ю- Поскольку её математическое ожидание равно нулю, т.е.

P ⁽ V) = У P^lV i = 0,

^—' ieN если дисперсия Е(р2) равна нулю, то Ii = у для всех i с N. Вероятность, что все индивидуальные индексы лежат в интервале [γ – ε, γ + ε] определяется равенством Чебышева

Е(р2)

Р(-£ < р < +г) >1--—.

Учитывая соотношение

D(x) = у(х,у)р(у,х), среднюю гармоническую величину можно принять в качестве метрической функции.

Поскольку агрегатные показатели связаны зависимостями:

A = yr,  I = yd, J = yrv, I = Аг, у = AI, rV, p = r2 = d,

то построим метрический треугольник ABC с опущенной из вершины прямого угла C высоты, определим его стороны

A = AC, I = AD, J = CD, y = AB, y-I = BD,

и введём обозначение L = CB . Данная величина равенством

J = rL

связана со структурными сдвигами. Если основное метрическое тождество Пифагора

A2 = I2 + J2

даёт возможность применять в оценке поведения объекта тригонометрический анализ, то c помощью метрического тождества

A2 =y2- L2

можно проводить анализ с помощью гиперболических функций.

Метрический треугольник появляется как результат качественного отклонения фактического состояния объекта от эталона. При J=0 имеем: DB = 0, AC = AB = AD, т.е. A = у = I, и состояния подобны. Это качественное расхождение можно оценить величиной отрезка DB = Е(р'). Дисперсия этой величины равна Е(р2) = у2 — A2 = L2. Её, например, можно взять целевым критерием в задаче оптимизации при условиях ограниченности ресурсов.

Пусть D(y) < D(η). Тогда I < λ < 1. Разность 1 – I определяет нереализованные возможности объекта по отношению эталона. По величине λ – I можно оценить потенциальное сближение, а величина (λ – I)/(1 – I) даёт оценку сближения фактического состояния с эталоном за счёт структурных сдвигов в общем объёме нереализованных возможностей.