Основные характеристики факельного континуума в зоне интенсивного горения котельного агрегата

Эффективность сжигания топлива и теплообмена в участках котельного агрегата (КА), как и минимизация вредных выбросов, в значительной мере формируются в начале газомеханического тракта КА и в системе подготовки компонентов горения. В свою очередь, компоновка КА и вид сжигаемого топлива должны быть согласованы с системой подготовки и подачи компонентов горения, конструкцией топливосжигающих устройств (ТСУ) и оформлением зоны интенсивного горения (ЗИГ). Таким образом, система подготовки и подачи компонентов горения, конструкция ТСУ формируют в ЗИГ условия устойчивого воспламенения и эффективного выгорания топлива, что связано с температурой факела и теплообменом в ЗИГ.

Достаточно широко применяемый в исследованиях анализ ситового состава топливной пыли основывается на расчете полного остатка по формуле Розина - Раммлера R ₅ = exp ( - b 5 n ) , где b и n -постоянные коэффициенты, характеризующие соответственно тонкость измельчения и однородность зернового состава топливной пыли. Применение характеристики полного остатка R ₅ удобно для сведения всех фракций пыли к 1,0 с учетом потерь при анализе, что отвечает закону сохранения массы. Этот анализ также соответствует принятой стандартной методике рассева дисперсных твердых частиц [1] и широко используется на практике.

Но, при движении в факельном континууме в процесс нагрева, выделения и горения летучих, горения кокса топливная пыль входит пофракци-онной смесью, начиная с мелких фракций с разме- ром δмин и заканчивая крупными фракциями с размером частиц δмакс. Поэтому для анализа тепловых и температурных процессов в факельном континууме необходимо связать анализ полного остатка с локальным значением фракции в ансамбле топливных частиц F(δi).

Обычно применяемая на практике методика основана на анализе фракционного состава для интервала значений δ от δ₁ до δ₂ F (δ₁/δ₂), что отвечает дискретному характеру процесса рассева топливной пыли. Для получения непрерывной зависимости F (δ _i ) необходимо выбрать представительную точку для интервала (δ₁; δ₂). Рекомендуемый в работе [2] метод фракционного анализа, когда F (δ + Δδ) делится на интервал изменения фракционного состава от δ до Δδ, то есть на Δδ, не отвечает задаче, так как, согласно определению, F [δ/(δ + Δδ)] = R (δ) – R (δ + Δδ), и далее

F [5Д5 + А5 )] _ R ( 5 ) - R ( 5 + А5 ) _

А5 = А5 = exp (-b5n) - exp (-b (5 + А5)n) А5

Для монотонно убывающей с увеличением δ величины полного остатка R (δ) формула (1) дает относительное снижение полного остатка на интервале [δ; δ + Δδ], который стандартно определяется в долях от общей массы топлива, то есть, формула (1) дает изменение полного остатка с изменением Δδ . Это скорость изменения полного остатка R (δ) на интервале изменения δ с изменением этого интервала, почти не связанная с изменением фракционного остатка на этом интервале.

Постановка задачи

Рационально для определения характерного значения фракционного остатка на интервале изменения размера δ применить среднюю арифметическую величину от двух интервалов F(δ1/δ2) и F(δ2/δ3), памятуя о том, что между средней ариф-m метической любой величины yar , средней геометрической ygm и средней гармонической ysm величинами существует соотношение у™ < у™ < у™ [4]. Отсюда

F_t = 0,5 [ F ( 5 1 / 5 2 ) + F ( 6 2 /5 з ) ] =

= 0,5 [exp ( - b 5 ^ ) - exp ( - b 5 П ) ] .             (2)

Полученные таким способом характерные точки F_i дают возможность сформировать непрерывную кривую фракционного состава ансамбля топливных частиц, что позволяет применить для математического описания поведения ансамбля частиц в топке дифференциальное и интегральное исчисление. Достоверность такого приближения, то есть, адекватность замены ступенчатой функции F [δ/(δ + Δδ)] непрерывной кривой F i увеличивается с увеличением числа замеров на ситах для рассева топливной пыли. Необходимо также учесть, что одной точке фракционного состава соответствует достаточно большое число частиц; так как 1 % от массы навески в 25 г фракции 200 мкм соответствует 330 частиц этого размера.

Возможно, точность и оперативность определения доли фракций в топливной пыли можно повысить с применением пневматического рассеивателя типа РП-5 [3], который позволяет выделять фракции, начиная с самой мелкой.

Разработка основных математических соотношений

Как показывает качественный анализ в рамках теории специальных распределений вероятностей [5], фракционный состав пыли твердого топлива можно описать уравнением гипергеометрического распределения, которое при увеличении числа замеров приводит к биномиальному распределению. При переходе к непрерывному распределению вероятностей, как показано выше, этому соответствует кривая Гаусса с плотностью нормального распределения вероятностей отклонения от среднего значения

ф ( u ) = exp ( - 0,5 u ²)/V2 n , (3) где в качестве аргумента введено u = (δ – ξ)/(ξ · σ) – стандартное нормальное отклонение; ξ соответствует размеру частиц δ , отвечающему максимуму на кривой F i = f (δ); σ² – дисперсия, σ – стандарт отклонения. Нормализация в данном случае означает размещение ансамбля топливных частиц по их числу около максимума ξ и приведение всех значений к безразмерному виду; стандартизация – определение характеристик ансамбля к виду зависимости от стандарта отклонений σ. Функция ошибок ф( u ) , которую в данном случае лучше назвать функцией отклонений, табулирована и приводится в справочниках [5]. Для условий рассматриваемой задачи функция отклонений изображена на рис. 1. Следует отметить, что стандартное отклонение как обобщающий аргумент однозначно определяет функцию (3) и значениям и = 1 и и = – 1 соответствуют точки перегиба на кривой, построенной по зависимости (3). Также по построенной в соответствии с фракционным со-

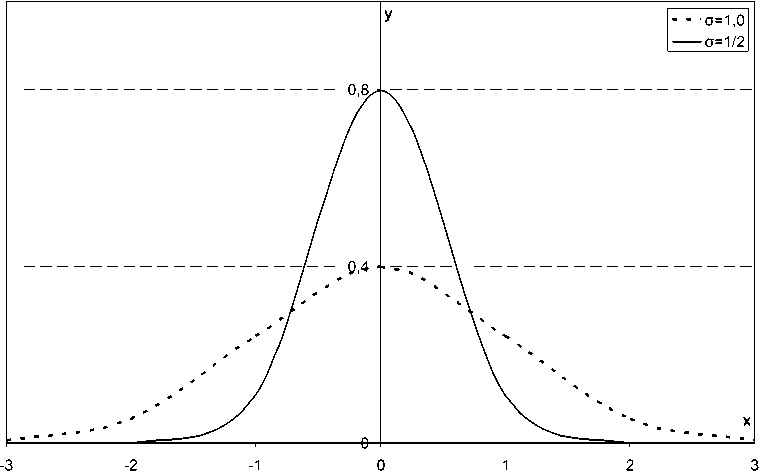
Рис. 1. Плотность распределения Гаусса нормализованной случайной величины у = φ( и ) , где х = и = (δ _i – ξ)/(ξ · σ) , с центром ξ и дисперсией σ ²

ставом кривой φ( и ) легко определяется дисперсия σ² = (δ – ξ)²/(ξ ·и )².

Достоверность описания практического распределения фракционного состава топливной пыли упр ≡ у1 уравнением кривой Гаусса (3), построенной по предложенной методике урасч ≡ у2, можно определить расчетом коэффициента корреляции ry1,y2, характеризующим тесноту линейной связи между у1 и у2. Для этого рационально зависимость (3) подвергнуть логарифмической линеаризации у2 = lnф(u) = -(0,92 + 0,5u2).               (4)

Определив обычным путем [5] коэффициент корреляции –1,0 ≤ r _1,2 ≤ 1,0 между практическими результатами по рассеву топливной пыли и кривой Гаусса, можно количественно оценить достоверность описания (3). Эту методику можно также применить на стадии определения F (δ i ) .

Ансамбль частиц топлива с характеристиками (1)–(3) движется совместно с потоком воздуха со скоростью w l , изменяющейся по длине факела l вследствие расширения факела и изменения его температуры и размеров из-за нагрева и выгорания топлива. Учесть расширение факела можно по падению средней кинетической энергии E_l / E ₀ = 0,56 d ₀/0,15 l для круглой струи с выходным диаметром топливо – сжигающего устройства d 0 [6]. Тогда для локальной скорости факельного континуума без учета изменения его температуры w_l ²= 3,73 w ₀ ² d ₀/ l , откуда w_l = 1,93 w ₀( l / d ₀)^–0,5. Аналогичные зависимости предложены для плоского и закрученного факелов.

Учет температурного фактора в изменении скорости по длине факела возможен в первом приближении на основе следующих соотношений. Так как El /E0 = ρw2/ρ0w02, то при выделении в величине ρw2 плотности потока массы ρw, которая согласно уравнению сплошности постоянна ρw = ρ0w0 = const, можно определить температурную зависимость El,T /E0 = (ρ0w0wT)/(ρ0w0w0) = wT/w0 и далее wt, T = 1,93 Wo (TT)(ljd 0 )-0,5.                (5)

Таким образом, в рамках поставленной задачи скорость факельного континуума растет пропорционально увеличению его абсолютной температуры и убывает обратно пропорционально корню квадратному из относительной длины в калибрах l / d 0 . Более точный учет температурного фактора возможен при расчете теплоты адвективных потоков массы, образующихся за счет эжекционного эффекта факела, и теплоты тепловыделения при сгорании топлива (advection – движение присоединенных масс, англ. [8]).

Согласование модели с факельными характеристиками

При адаптации соотношений полифракцион-ного потока топлива к аэромеханике факельного континуума необходимо уточнить два условия асимптотического характера, которые связаны с начальным и конечным участками факела. Предельное минимальное значение координаты ипр, соответствующее размеру частицы топливной пыли δпр, которая еще не участвует в нагреве, воспламенении и не учитывается в расчете, определяется по формуле ипр = (δпр – ξ)/(ξ·σ). Если расположить сечение факела lф = 0 в месте начала смешения топливного потока с воздухом и принять для этого сечения δпр =0, тогда ипр = –ξ/(ξ·σ), то есть, расположение начального сечения факельного континуума зависит от фракционных характеристик ансамбля топливной пыли.

Частицы топлива, имеющие малую термическую массивность (число Bi ≤ 0,1) нагреваются практически без перепада температуры по сечению частицы, поэтому безразмерную температуру Θ частицы с диаметром δ _i можно описать зависимостью

0 = exp ( -3BiFo ) , (6) где Bi = αδ _i /λ, Fo= a τ / δ _i ²; λ, ρ, c , a = λ/ρ c – теплопроводность, плотность, массовая теплоемкость материала частицы в согласованных единицах. Как показывает численный анализ, при нагреве крупных топливных частиц с высокой интенсивностью теплоотдачи число Bi может превышать значение 0,1. Влияние термической массивности частиц на температурное поле (6) можно учесть введением коэффициента термической массивности.

Коэффициент термической массивности топливной частицы m определяется отношением коэффициента теплоотдачи на поверхность топливной частицы α и коэффициента теплопередачи k, причем в k входит только часть внутреннего термического сопротивления с учетом коэффициента формы частицы σ m = 1+aS/ 2X(^+2) = a[ya+0,55/X(^+2)] =

= 1 + 0,5Bi/ ( g + 2 ) . (7)

В сферическом приближении топливной частицы σ=3 и m = 1 +0,1 Bi, при максимальном значении Bi= 1,0 коэффициент термической массивности в этом случае равен m = 1,10. Если принять коэффициент теплопроводности угольной частицы равным λ = 0,15 Вт/м·К, то для частицы размером 50 мкм = 0,05·10–3 м при коэффициенте теплоотдачи на поверхность частицы α = 100 Вт/м2·К можно получить Bimin = 0,03, m = 1,003, что относится к области термически тонких тел. При этих же условиях частица максимального размера δ = 1000 мкм= 1·10–3 м будет соответствовать числу Bimax = 0,67, при этом отклонение от расчета температурного поля частицы по закономерностям термически тонкого тела достигнет 6,7 % при коэффициенте массивности m = 1,067. Время нагрева до заданной температуры интенсивного выделения летучих веществ необходимо рассчитывать по формуле, полученной логарифмированием зависимости (7)

Тинт = [5Рст/ (М)] In(00/бинт ), (8) где θ0 = tг– t0 – разность температур между топочными газами tг и начальной температурой частицы t0; θинт = tг – tинт – разность температур между топочными газами и температурой интенсивного выделения летучих. В первом приближении можно считать tинт температурой воспламенения горючей смеси. С повышением tинт разность температур θинт снижается и требуемое время τинт увеличивается; согласно результатам работы [6] время сушки час- тицы топлива можно не учитывать.

Последовательному характеру вступления частиц топлива в процессы теплообмена в факеле и аддитивной зависимости общего теплосодержания отвечает интеграл от функции распределения вероятности отклонений (3), причем пределы ин- тегрирования рационально установить от –∞ до максимального значения размера топливной частицы δmax, соответствующего верхнему пределу интегрирования U,

^Ф ( ⁵ ) =

1    ⁵ max

eV2л Д

’ 5 =

= Ф ( U ) .                                    (9)

Причем нормальная функция распределения

Ф u ( U связана с интегралом вероятностей Ф ( U ) и функцией ошибок erf( U /2^0,5) зависимостью

Ф _u ( U ) - 1/2 = 0,5erf ( U /V2 ) = Ф ( U ) .    (10)

Таким образом, нормальная функция распределения Ф(U) может быть определена через интеграл вероятностей Ф(U) или через функцию ошибок erf (и/V2), обе эти зависимости табулированы [4]. Но при практической адаптации этих зависимостей есть особенности, которые связаны с достоверностью применяемых зависимостей. Эти особенности можно определить на основе анализа результатов численного анализа зависимостей (8)–(9) при изменении интервалов варьирования аргументов и их функций. На рис. 2 показана функция распределения Фи(U).

Численный анализ показывает, что при применении интеграла вероятностей (9) для области положительных и отрицательных значений u = (δ – ξ)/(ξ·σ) разность между Φ(U) и Φ(δ) не превышает 0,10 % во всем интервале изменения и, в то время как при расчете Φu(U) по зависимости (10) разность может превышать 10 % в области отрицательных значений и, что связано с нижним пределом интегрирования при получении функции ошибок erf (U/ V2) = 2/ 7П Jo exp(-[и/V2]2"diu . (11)

Нижний предел интегрирования определяется фракционным составом топливных частиц в области малых значений δ и имеет важное значение для расчета процессов воспламенения топливновоздушной смеси, а верхний предел связан с расчетом недожога топлива при заданной длине факела, либо с определением требуемой длины факела при заданном недожоге топлива, что также связано с фракционным составом топлива в области больших значений δ.

Полученная интегральная функция связана с известным интегралом вероятностей [5], который приводится в справочниках в виде таблиц, она позволяет рассчитать не только полный остаток по

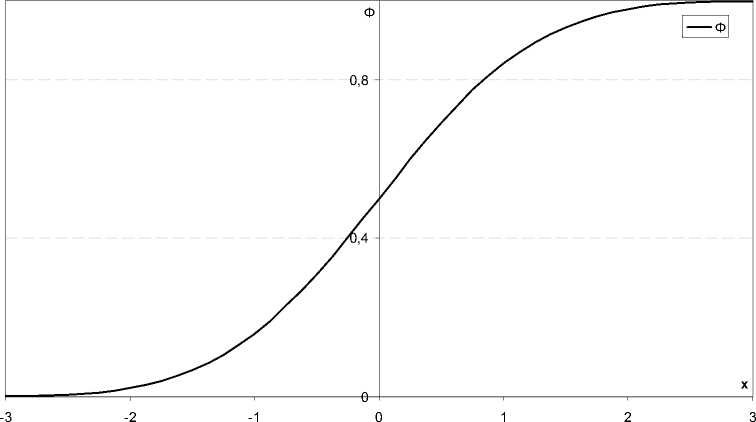
Рис. 2. Нормальная функция распределения Ф случайной величины х = и = (б _ ^)/(^ • _a)

известному фракционному составу, но и определить ряд свойств полифракционного топливного факела. Так, приведенная зависимость (8) позволяет определить наступление определенного температурного режима в зависимости от размера частицы и условий движения ее с полифракционным факелом. Для того, чтобы определить выгорание частиц топлива различного размера, к принятой схеме необходимо добавить условия взаимодействия горящей частицы с потоком топочной и факельной среды.

Если принять схему взаимодействия горящей частицы топлива с топочной средой [6] по плоскостной модели, что отвечает плоскому диффузионному слою между сферической частицей и топочной средой, то скорость выгорания частицы можно определить при G_c = const по уравнению d δ/ dτ = = –2 M_cG_c /ρ, при этом М_с = 12 кг/кмоль – молярная масса углерода, ρ ≈ 800 кг/м³ – плотность кокса. Принятая схема поверхностного одномерного горения по первичной реакции с образованием СО 2 имеет первый порядок по кислороду, горение считается квазистационарным и автомодельным во времени. При этом полное время выгорания частицы начального размера δ 0 :

. S So t = -J (p/Gc ^S = 0,04171 (p/Gc^S - <12> 2Мс s0 s

При подстановке в (7) времени τ в интегральном выражении для процесса, связанного с нагревом и горением топлива в факеле можно получить функцию распределения тепловыделения в факеле по его длине. Но эта схема требует уточнения как в части допущения сферических поверхностей плоскими, так и в части зависимости G_c от δ.

Учет полидисперсности среды в факельном континууме требует применения зависимости для функции выгорания одиночной частицы, связанной с локальным значением кинетических и диффузионных характеристик процесса. В первом приближении можно пренебречь влиянием горения СО в пределах пограничного слоя, восстановительными реакциями и внутренним реагированием [6]. Тогда для одномерной модели процесса горения первого порядка реакции по кислороду, находящемуся в недостатке, получается зависимость для потока выгорающего углерода G_c : G_c = ωС _ок, где ω – параметр кинетичности процесса выгорания топлива, определяемый в соответствии со вторым электротехническим правилом Кирхгофа для параллельной цепи из двух проводимостей. Функция окисления определяется количеством кислорода в факельном газе 0,21 Р г / RT и его расходом на горение летучих веществ и углерода по стехиометрическим соотношениям.

Учет динамики горения частиц

Динамика горения полифракционного топлива связана с распределением температуры и кон- центраций компонентов по длине факельного континуума; применение электротепловой аналогии и электрофизических правил Кирхгофа для узлов и цепей позволяет связать между собой ряд факторов. Обозначив узлами точки на поверхности горящей частицы, где окислитель отсутствует Сок = 0, и на внешней поверхности диффузионного пограничного слоя, где концентрация окислителя равна таковой в факельном континууме Софк , по- лучим разность потенциалов переноса окислителя А Сок = Сфк - 0=Сфк . Расположив параллельно распределенное диффузионное сопротивление 1/αD и сосредоточенное кинетическое сопротивление 1/k1, получим общее диффузионно-кинетическое сопротивление процессу горения RΣ= 1/αD + 1/k1 = = 1/ω, где диффузионно-кинетическая проводимость ω= 1/RΣ = αDk1/(αD + k1).

Фактор ω также можно назвать показателем кинетичности процесса выгорания топлива ωк, при aD»к 1, когда диффузионные процессы не ограничивают скорость горения, ωк = 1,0; при aD ^ к 1, когда лимитирующими становятся диффузионные процессы, ωк→0. При αD = k1 ωк = k1/2, что отвечает промежуточному режиму; таким образом, применение показателя кинетич-ности процесса горения ωк позволяет формально обозначить границы кинетического и диффузионного режимов с включением промежуточной области, что отвечает трансрежимным представлениям в части динамики процесса выгорания твердого топлива.

Локальная концентрация кислорода в факельном континууме Софк , кмоль/м3, определяется через начальную объемную концентрацию Сок.н, связанную со способом сжигания и конструкцией горелки – с применением воздушного дутья Сок.н = 0,21, и с расходом кислорода на горение летучих и кокса по кислородному балансу

_С ф = СР V ^ок     RTV _г

V ⁰

( а — 1 ) + K н .

V _

В (13) учтено, что стехиометрический расход воздуха V ⁰, м³/кг топлива, равен расходу на горение кокса и летучих V ⁰ = V к ⁰ K ^р + V л ⁰ V л ^р. Содержание кислорода согласно (13) обеспечивает локальное выгорание топливной частицы начальным размером δ _i по этой зависимости без учета переменности кинетического фактора [6]

d S, ₌ _2 М ф ^ к^ок d ^T      Р к

Диффузионный коэффициент массоотдачи αD определяется в общем случае через зависимость NuD от чисел Re и Pr, причем в качестве определяющей в число Re входит относительная скорость частицы в потоке. При развитии факельного потока относительная скорость и число Re падают до нуля, при этом NuD ≈2. Таким образом, показатель кинетичности процесса горения частиц топлива при этих условиях определяется по формуле wwK = k1Nu DD I 5 i /[ k1 + NuDD I 5 i) =

= 2 k 1 D / 5 i I ( k 1 + 2 D / 5 i ) .                   (15)

С учетом (13)–(15) скорость сгорания частицы топлива размером δi определится по формуле d5i _2 M 2k1 D/5i dt = pK (ki + 2D/5/

ЗИГ, изменения скорости вследствие изменения состава потока из-за горения и изменения температуры факельной среды от Т0 до Тф. Таким образом, изменение скорости факельной среды в процессе ее движения с горением от Lф = 0 до Lф = 1,0 можно представить зависимостью иф = wokFkykT , (19)

где k F , k V , k T – факторы влияния изменения сечения факела, изменения объемного расхода среды в фа-

келе и изменения его температуры соответственно:

C РV ⁰

^ ок.н Т к RTV _г

( a-1 ) V— + K_H ¹

0 ^н

V _к

—I

В

■ юк у

.

k F = /        Г^2;

( 1 + 0,21 1 ф/ d о )

В зависимости (16) в параметр В включены все константы конкретной задачи, доля несгорев-

^kV = г"

шего кокса K _н ^р принимается одинаковой для час-

тицы любого размера, температуру факельного континуума Т можно связать с абсциссой Х и длиной факела, таким образом, влияние фракционного состава сосредоточено в факторе ω к . Это позволяет разделить дифференциалы и проинтегрировать зависимость (16) с получением функции выгорания топливных частиц размером δ _i .

Г г“ 1+ ь» ^ф I у^а

V в

-1

;

к т = Т ф / Т о = 1+ А Т г_Ор Ь ф / Т о .

т выг

Т ^ 2D + ki5       Т Г 5io d 5, =+

В^  2 k.D i В k 4 D

5i0        1                     V 1

. (17)

Смена знака в (17) связана с изменением пределов интегрирования от 0 до δ _{i 0}, что соответствует динамике выгорания частиц топлива. Температура факельного континуума, влияющая на время

выгорания частиц топлива, в рамках задачи определяется аппроксимацией от Т инт = t инт + 273 до Т кон , соответствующей конечному сечению факела L ф = 1,0

Т = Т инт + L ф ( Т кон - Т инт ) . (18)

Продольные габариты факельного континуума можно определить с применением диагностических методик различного теплофизического содержания: аэромеханического, температурнорадиационного, концентрационно-аналитического характера, а также с применением методик математической статистики. Выбранный диагностический метод при этом должен соответствовать основной задаче исследования. В настоящей работе характеристики факела определяются на основе дисперсионного анализа топливной пыли, поэтому начальный участок факела l ₀ рационально определить по моменту воспламенения самых мелких частиц топливной пыли, согласно (8). При этом l ₀ будет отличаться от расстояния до устья горелки на величину, требуемую для прогрева и воспламенения самых мелких частиц пыли.

Основная задача в рамках поставленных условий заключается в определении степени влияния на начальную скорость на выходе из сопла F 0 = π r 0 ² в основном трех факторов: расширения струи вследствие вовлечения в поток среды из

Соотношение (20) получено из геометрических соображений, основанных на экспериментально измеренных центральных углах раскрытия гетерогенного факела, равных 12°, при этом учитывались адвективные потоки массы. Соотношения (21)–(22) допускают линейную аппроксимацию зависимости Ф = f ( X ), связанную с выгоранием топлива и повышением температуры в факеле, как показано на рис. 3. Фактор l ф / d ₀ является расстоянием от сопла в калибрах, здесь применен этот фактор, так как до плоскости начала воспламенения топлива развитие факельной струи идет по законам аэромеханики без внутренних источников теплоты. Фактор Δ Т гор учитывает эффект увеличения температуры факела за счет реакции горения топлива.

После воспламенения топлива при L ф = 0 пофракционное выгорание топлива и повышение температуры факельного континуума идет в соответствии с интегральной кривой Ф= f ( X ), но учет этого фактора делает задачу итеративной, поэтому возможным решением является линейная аппроксимация Ф = f ( X ), так как зависимости (20)–(22) описывают факторы второго порядка влияния. Собственно, эти аппроксимации являются следствием разложения функции V ( L ф ) , как показано

ниже.

Количество газообразной фазы в факельном континууме V _г, м³/кг топлива, изменяется от α V ⁰ в начале факела при L ф = 0 до воспламенения с (α–1) V ⁰ + V г ^α=1 при завершении горения в конце факела, где L ф = 1,0. При разложении функции V г ( L ф ) в ряд Тейлора первые два слагаемых ряда дают

V _r ( L ф ) = a V ⁰ + L

d V _r ^a= 1 '^ф d L ф

.

Входящие в формулу (23) переменные V ⁰ и

V _г ^{α= 1} определяются справочными данными для

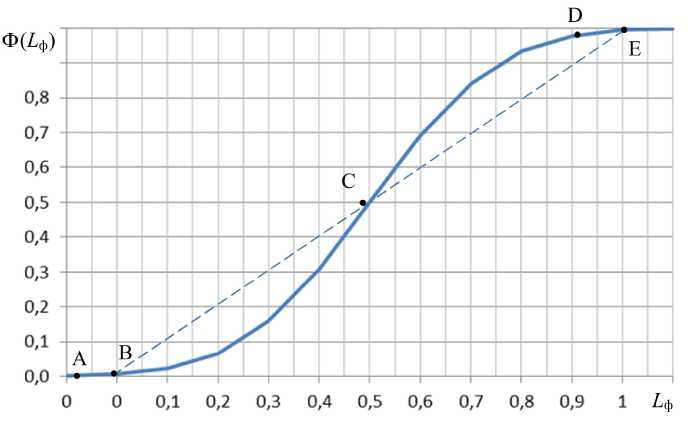
Рис. 3. Изменение интегральной функции Ф( L ф ) по длине факела L ф : линия А–В – начальный участок факела до воспламенения; точка В – начало горения, точки D, Е – завершение горения с заданной степенью недожога; пунктирная линия В–Е линейная аппроксимация степени выгорания топлива

конкретного вида твердого топлива [9] при 0 ≤ L ф ≤ 1,0. Аналогичным образом определяется энтальпия факельного континуума в функции изменения его температуры, причем изменения температуры можно в первом приближении определить по изменению энтальпии при с_р = const .

Определенные таким образом границы факела позволяют нанести на координате Х точки начала и конца факельного континуума и, в соответствии с этим, на координате Ф найти начало и конец факела как источника тепловыделения с учетом начального участка факела. Поправки в скорость факельного континуума (19) вводятся последовательно: на участке от l ф =0 до l ф = l н вводится только поправка k_F , затем вводятся все три поправки вплоть до конечных сечений факела.

Протяженность начального участка до начала воспламенения l _н = l _н.к d ₀ зависит от начальной скорости факельного потока w ₀ и интенсивности теплоотдачи в конвективном выражении α, Вт/м²К, что при учете только k_F дает

1 3_K + 9,5238 1 2_K + 11,3378d _o l _{H к} = н.к н.к 0 н.к

= 56,44 w ₀ ( dd ₀ a ) (24) или при применении безразмерных чисел подобия Re = w ₀ d ₀/ ν и Nu = α d ₀/λ

1 3_K + 9,5238 1^ +11,3378 d_n1 = н,к н,к н,к

= 40,6368Re/ d ₀Nu. (25)

Решить уравнение (24) можно либо методом Кардано, либо численно; адаптационные расчеты показывают, что длина начального участка составляет (0,95…1,30) l _н.к, что удовлетворительно согласуется с экспериментальными данными.

Произведенные преобразования с абсциссой на рис. 3 позволяют численно определить функ- цию Ф на ординате графика как интегральную функцию увеличения энтальпии факельного континуума, что можно связать с его адиабатической температурой

Qр tад Ф (Lф ) у . (26) срVг

Подстановка в формулу (26) располагаемой теплоты топливного потока Q ^р _р и выхода продуктов сгорания с единицы топливной массы V _г при теплоемкости продуктов сгорания с_р позволяет определить локальное значение адиабатической температуры факельного континуума t _ад при умножении полученного результата на нормальную функцию отклонений Ф( L ф ) для данной координаты L ф [5]. Переход от Ф( U ) согласно рис. 2 к Ф( L ф ) на рис. 3 осуществляется расчетом времени поф-ракционного выгорания по (17), которое соответствует времени, определенному по фактической скорости частиц в факеле τ = l ф /w ф по (19). Полученная зависимость решается относительно связи l ф с и = (δ i – ξ)/(ξ · σ).

Заключение

Применение нового метода математического описания поведения ансамбля полидисперсного потока топливных частиц в процессе горения позволило определить функцию пофракционного выгорания и связанные с ней энтальпию и локальную адиабатическую температуру факельного континуума.

Определена протяженность начального участка факела lн, где топливо еще не воспламенилось, которая зависит от интенсивности подвода тепла к начальному участку α, принятой температуры ин- тенсивного выделения летучих веществ tинт, скорости потока на выходе из горелки w0 и ее изменения с повышением температуры и раскрытием факела.

Время выгорания частиц размером δ i поли-фракционного потока зависит от характеристик топлива и параметра кинетичности процесса горения ω_к при учете влияния температуры факельного континуума Т ф .