Основные и сопряженные уравнения диффузии
Автор: Мурадов Ф.А., Набиева С.С.
Журнал: Теория и практика современной науки @modern-j
Рубрика: Основной раздел
Статья в выпуске: 7 (25), 2017 года.
Бесплатный доступ
Бу маколада манбаадан(источник деб таржима) чикаётган захарли моддаларнинг таркалиш ва диффузия жараёнининг асосий ва тескари(сорряженные таржима) масалалари каралган. Решение проблемы об оценке загрязнения атмосферы и подстилающей поверхности пассивными и активными примесями, о математическом моделировании оптимизационных проблем, связанных с охраной окружающей среды связано с решением уравнения переноса и диффузии и задач оптимизации.
Математическая модель, перенос и диффузия вредных веществ, погодно-климатический фактор, гидромеханика, численный алгоритм, краевая задача
Короткий адрес: https://sciup.org/140272096
IDR: 140272096
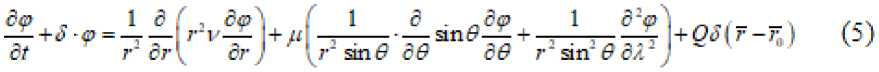
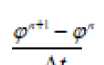
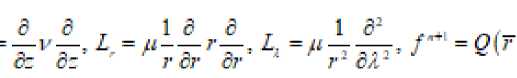
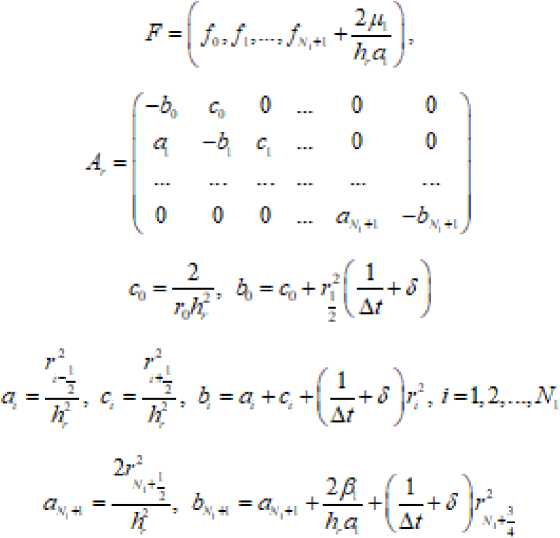
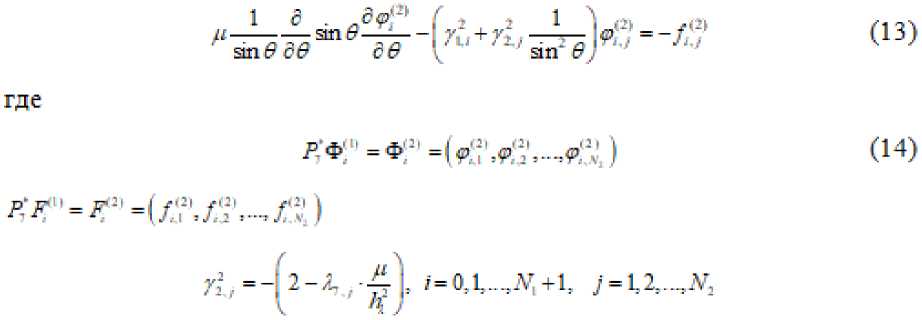
Список литературы Основные и сопряженные уравнения диффузии
- Ravshanov N., Sharipov D., Muradov F. Computational experiment for forecasting and monitoring the environmental condition of industrial regions // Theoretical & Applied Science: International Scientific Journal. - 2016. - Vol. 35. - Issue 3. - Pp. 132-139. - DOI: 10.15863/TAS.2016.03.35.22
- Копченова Н.В., Марон И. А. Вычислителная математика в примерах и задачах. - М.: Наука, 2008. - 368 с.
- Равшанов Н., Шарипов Д.К., Ахмедов Д. Моделирования процесса загрязнения окружающей среды с учетом рельефа местности погодно-климатических факторов // Информационные технологии моделирования и управления - Воронеж, 2015.№3. - С. 222-235.
- Фаддеева В.Н. Метод прямых в применении к некоторым краевым задачам//Труды Математического института АН СССР им. В.А. Стеклова, т. XXVIII (28), М., 1949.
