Основные методы расчетов, применяемые в механике грунтов

Среди численных методов расчета в механике грунтов чаще всего используют МКР (метод конечных разностей) и МКЭ (метод конечных элементов), на основании которых решаются такие задачи как консолидация, ползучесть, динамика грунтов, математически моделируются поведение грунтовых массивов, взаимодействующих с сооружениями, с учетом практически всех присущих грунтам особенностей.

Для обеспечения простоты и сокращения времени расчетов на основе этих методов разрабатываются вычислительные программы или программные комплексы, которые ориентированы на решение определенных задач. Универсальный характер расчетных комплексов позволяет решать множество задач данного класса, то есть необходимо просто внести параметры конкретной задачи в исходную информацию, что не требуют изменения всего алгоритма решения, в чем и заключается важнейшее преимущество численных перед аналитическими решениями, каждое из которых справедливо в рамках конкретной задачи.

МКР ориентируется на решение задач, которые описываются уравнениями в частных производных, применяемых для решения задач теории предельного равновесия, а сама идея метода подразумевает замену частных производных в дифференциальных уравнениях решаемой задачи отношениями разностей переменных (конечными разностями).

МКЭ является одним из основных методов решения задач, которые описываются дифференциальными уравнениями и часто применяется для решения задач механики грунтов. Расчетная область разбивается на конечные элементы и может представлять собой грунтовый массив, систему типа фундамент – основание или сооружение – основание и т.п. Сами элементы представляют собой одномерные, плоские или пространственные фигуры простой формы, такие как прямолинейные или криволинейные треугольники и четырехугольники (рис. 1).

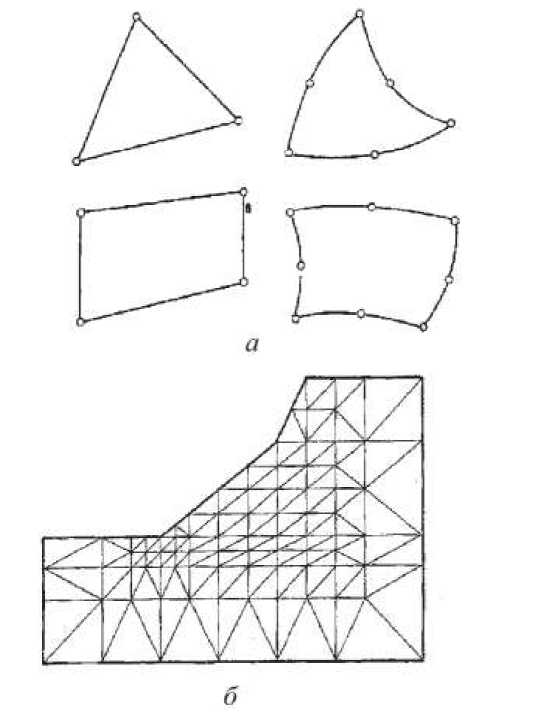
Рис. 1. Некоторые типы плоских конечных элементов (а) и пример конечно-элементной дискретизации плоской расчетной области (б)

Узлы или узловые точки, которые выделяются в элементах размещаются в вершинах элементов, а так же могут быть расположены на сторонах и внутри элемента, а сами элементы имеют общие узлы и стороны. Расчетная среда в процессе деформации остается сплошной и непрерывной, а сама разбивка является только математическим приемом и не сопровождается механическим разделением. Так как в механике грунтов исследуют практически не ограниченный в размерах грунтовых массив, который взаимодействует с сооружением, а для расчета МКР и МКЭ рассматриваются области конечных размеров, то приходится ограничивать размер рассматриваемого участка массива, но таким образом, чтобы влияние искусственно введенных границ не приводило к существенному искажению результатов решения. Краевые задачи для неоднородных сред, характер неоднородности которых связан с наличием в расчетной области участков с различными физико-механическими свойствами материалов, так же можно решать численными методами. Точность конечных результатов зависит от качества сетки, а граничные условия назначают с учетом особенностей решаемой задачи [1].

Наиболее часто используются следующие модели:

• -    местных упругих деформаций;

• -    упругого полупространства;

• -    нелинейно-деформируемого полупространства.

Модели совершенно по-разному влияют на контактные напряжения, что можно продемонстрировать на примере (рис.2.).

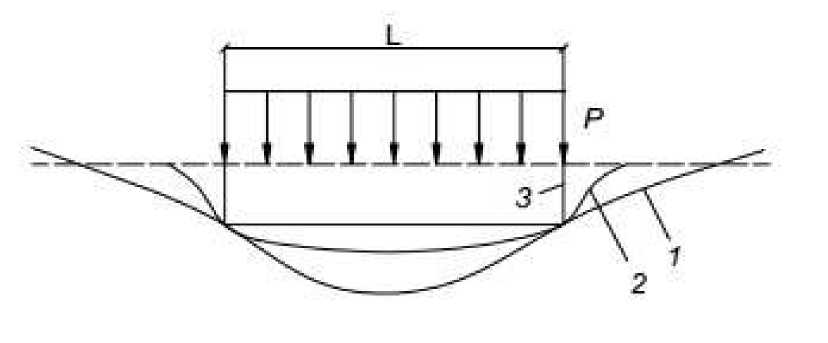
Рис.2. Характер прогиба поверхности грунта при действии полосовой нагрузки. 1- упругое полупространство; 2- нелинейно-деформируемое полупространство; 3- модель местных упругих деформаций.

Если на поверхность грунтового полупространства действует нагрузка по полосе, то образуется лунка оседания грунта различной формы и размеров.

На поверхности линейно-деформируемого полупространства лунка имеет пологий характер. Проявляется высокая распределительная способность массива и распространяется за пределы полосы нагружения. На поверхности нелинейно-деформируемого полупространства лунка имеет более крутой угол наклона и сравнительно-равномерное оседание в центральной части. По модели местных упругих деформаций лунка имеет прямоугольную форму, что говорит об отсутствии распределительной способности основания.