Основные принципы и уравнения, определяющие природу дихотомического ветвления магистральных артерий.

Поражение атеросклеротическим процессом стенки артерий особенно выражено в области ее бифуркации [1,2]. Это объясняется тем, что кровоток в области ветвления артерий отличается от ламинарного [3, 4]. В результате формирования турбулентного кровотока и зон рециркуляции изменяются механические свойства стенки артерий, увеличивается проницаемость эндотелия для крупных молекул и пропитывание стенки сосуда плазмой. Атеросклеротические бляшки начиная с ранней стадии могут осложняться адгезией и агрегацией тромбоцитов [5]. На современном этапе развития науки ряд исследователей полагает, что гемодинамический фактор, а также морфология атеросклеротической бляшки и геометрия артерий играют важную роль в прогрессировании атеросклеротического процесса, вызывая интимальное повреждение и дисфункцию эндотелия, особенно в области бифуркации артерий. Дисфункция эндотелия - это дисбаланс между медиаторами, обеспечивающими в норме оптимальное течение всех эндотелийзависимых процессов, что является важнейшим патогенетическим фактором, способствующим прогрессированию атеросклероза [5, 6, 7].

Цель нашего исследования - оценить влияние гемодинамического фактора на стеноти-ческий процесс, выявить математические связи между геометрическими параметрами каналов и характеристиками вращательно-поступательного движения крови в них.

МАТЕРИАЛ И МЕТОДЫ

В исследование включены 2 группы пациентов. Первая (контрольная) группа - 26 пациентов без атеросклеротического поражения бифуркации сонных артерий. Мужчин - 20, женщин -6 человек, средний возраст 50,2±5,3 лет. Вторая группа - 36 пациентов с атеросклеротическими стенозами сонных артерий. Мужчин - 28, женщин - 8, средний возраст 55,8±5,8 лет. Проведено дуплексное сканирование артерий шеи (определяли средние линейные скорости в об щей, внутренней и наружной сонных артериях). Используя данные мультиспиральной компьютерной ангиографии, мы измеряли диаметры общей, внутренней и наружной сонных артерий и углов ветвления наружной и внутренней сонных артерий. Степень стеноза определяли согласно классификации ECST [8].

Точки измерения диаметров сонных артерий были стандартизованы и определялись на расстоянии 1 см от бифуркации общей сонной артерии, т. е. в зоне формирования атеросклеротических бляшек. Средние линейные скорости кровотока в сонных артериях также определялись в этих зонах.

Данные, полученные у пациентов контрольной группы при дуплексном сканировании и мультиспиральной компьютерной ангиографии, подставляли в формулы (8), (9) и (11). На рис. 1 представлено измерение углов ветвления и диаметров наружной, внутренней и общей сонных артерий по данным МСКТ ангиографии.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

В качестве геометрических параметров использовали площади поперечных сечений ма-

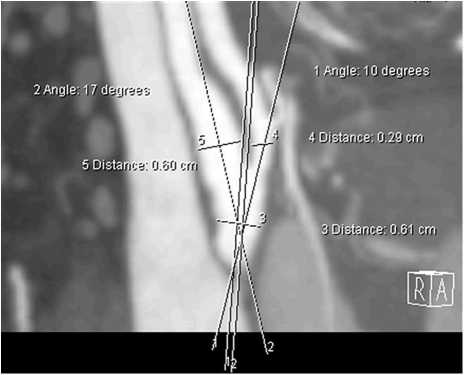
Рис. 1. Измерение углов ветвления и диаметров наружной, внутренней и общей сонных артерий по данным МСКТ ангиографии.

теринского SO и двух дочерних каналов S1, S2, а также углы ветвления последних 01,02. Закрученные потоки крови в трех сопряженных каналах характеризовали поступательными скоростями движения Uo, иг U2 и, соответственно, вращательными Wo, Wv \N2 [9]. Поскольку в кровеносных сосудах в области бифуркации такие характеристики кровотока, как скорость и направление, испытывают существенные изменения, казалось бы, это должно приводить к дополнительной силовой нагрузке на транспортные каналы в области ветвления. Однако живая система уже в процессе формирования архитектоники кровеносного русла стремится максимально исключить любую излишнюю силовую нагрузку путем ее равномерного распределения [9, 10]. На языке гидродинамики результатом этого стремления в рассматриваемой задаче является уравновешивание сил и моментов сил, действующих на сосудистую стенку. Именно таким образом в ветвящемся кровеносном русле обеспечивается отсутствие эффектов нескомпенсированной силовой отдачи. В терминах математической физики выдвинутые положения с использованием локального динамического подхода пред ставляются следующей системой уравнений [9]: R02U0=R22U2(1)

R02U0 = R^U,2 cos Д + R22U2 cos Д2(2)

R/U/sin^ = R22U22 sin Д2(3)

R/UjWj sin Д = R23U2W2 sin Д2(4)

R03U0W0 = R^UjWj cos Д + R23U2W2 cos /Л + +R0(R12U12 sin Д + R22U2 sin Д2(5)

u02+w02=u12+w12

U02+W02 =U22+W22(7)

Система уравнений (1)-(7) описывает преемственное поведение закрученных потоков крови в области бифуркации артерии с учетом несжимаемости жидкости [9]. В представленных уравнениях параметры Ro, Rv R2 соответствуют радиусам материнского и двух дочерних каналов. Уравнение (1) системы отвечает закону сохранения расхода массы крови в единицу времени до и после ветвления. Уравнения (2) и (3) представляют закон сохранения потока количества движения, выраженный равенствами проекций векторных величин на ось материнского канала и, соответственно, на ось, перпендикулярную ей. Напротив, если при пе реходе через узел ветвления сосудов поток количества движения в единицу времени испытывает скачок, это означает, что в указанном участке сосудов будет постоянно присутствовать силовое напряжение. Уравнение (4) и (5) соответствует закону сохранения потоком момента количества движения. Уравнение (4) указывает на отсутствие момента сил, приводящего к скручиванию сосудов ветвления относительно оси, проведенной через узел бифуркации перпендикулярно оси материнской артерии. Для сохранения потоком момента количества движения вдоль оси материнского канала принципиальным является факт пространственного винтового ветвления дочерних сосудов. Поскольку оси последних не лежат в одной плоскости, а пространственно разнесены, часть исходного потока момента импульса в единицу времени расходуется на преодоление реально действующего момента сил. Это обстоятельство учтено в уравнении (5), в правую часть которого введено дополнительное слагаемое. Необходимо отметить, что действие указанного момента сил наиболее существенно, когда поступательная скорость кровотока максимальна. Именно в этом случае динамическая нагрузка на узел бифуркации наибольшая. В связи с импульсным характером кровотока под Uo, Ur U2 понимают максимальные значения поступательной скорости крови в артериях. Уравнения (6) и (7) соответствуют закону Бернулли, в котором изменением давления внешних сил в области узла бифуркации пренебрегают. Таким образом, вся система уравнений (1)-(7), описывающая узел ветвления магистральных кровеносных сосудов, характеризуется одиннадцатью параметрами: Uo, Wo, Ц, Wr U2, W2, Ro, Rv R2, 0r 02. Если мы знаем четыре из них: Uo, Wo, Ro, 0V - система уравнений позволяет определить остальные параметры. Закономерные математические связи между параметрами потоков крови и геометрическими характеристиками ветвления сосудов имеют простой для анализа вид и наглядную интерпретацию [9]. Поскольку представленные уравнения однородны относительно параметров поступательной скорости крови в каналах, это позволяет легко исключить их из рассмотрения путем соответствующих подстановок и получить одно из важных соотношений искомой закономерной связи. Действительно, выразив произведение:

R/Ц2 =R22U22

sin/?2 sin/?.

Ишемическая болезнь сердца из уравнения (3) и подставив его в уравнение (2), получим:

U _=и ^Ro /   sin Д,

1  °^^т(Д+Д2)

Далее, используя вновь уравнение (3), найдем:

и,=иЛ I sinA

"R^sin^+Д|     (9)

Подстановка в уравнение (1) U1 и U2 из соотношений (8) и (9) позволяет получить математическую зависимость, устанавливающую связь между радиусами сосудов и углами их ветвления:

R_o^/sinCMPJ = ^RiV^PJ ^{+ R}2V^P3 (10)

Используя значения диаметров материнского и дочерних сосудов, уравнение (10) можно представить в таком виде:

Dj I sin/?2 D2 / sin Д П0^8т(Д+Д2) П0^8т(Д+Д2)    (11)

Используя уравнения (8), (9) и (11), мы провели собственное исследование.

Среднее значение коэффициента ветвления, полученное в ходе математических действий при использовании формулы (11) в контрольной группе (п=52), составило 1,024+0,12 и приближалось к 1, различия отсутствуют (р>0,05).

Среднее значение линейной скорости в наружной сонной артерии (Vcp. НСА), рассчитанное с использованием уравнения (9), у пациентов группы контроля составило 49,86±7,58 см/с, зарегистрированное при ультразвуковом исследовании - 51,85±7,7 см/с. Достоверных различий также не выявлено (р>0,05) (табл. 1).

Учитывая полученные результаты, у 36 пациентов (п=72) с атеросклеротическим стенозом сонных артерий проведен регрессионный анализ (табл. 2, рис. 2). Выявлена корреляционная связь между степенью стеноза (61,4± ±14,9%) и коэффициентом ветвления (0,8± ±0,24), рассчитанным по формуле (11). Коэффициент корреляции г=0,58 (умеренная корреляция), р<0,05. Также выявлена корреляционная связь степени стеноза с разностью значений линейной скорости кровотока во внутренней сонной артерии (DVcp. ВСА), полученной при дуплексном сканировании и рассчитанной по формуле (8). Коэффициент корреляции г=0,56 (умеренная корреляция), р<0,05.

На основании представленных данных была проведена оценка чувствительности и специфичности теста - зависимость коэффициента

Таблица 1

Средние значения линейной скорости во внутренней и наружной сонной артериях, полученные при дуплексном сканировании и рассчитанные по формулам (8) и (9) у пациентов контрольной группы (п=52)

Параметры Дуплекс артерий Расчетные данные Vcp., см/с ВСА 32,05±5,52 29,38±5,95 НСА 51,85±7,7 49,86±7,58 р>0,05

Таблица 2

Данные регрессионного анализа между степенью стеноза (п=72), коэффициентом ветвления и разностью линейной скорости кровотока во внутренней сонной артерии

Стеноз (61,4±14,9%)

Коэффициент ветвления (0,8±0,24)	AVcp.BCA (51,35±41,4)
г=0,58	г=0,56
р<0,05	р<0,05

Стеноз ВСА=77,3121-29,245 хХ+0,1475 х Y

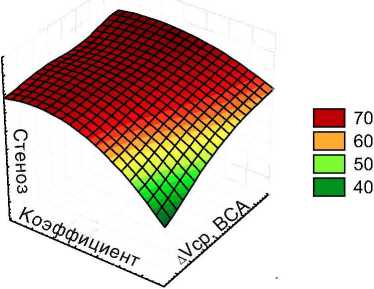
Рис. 2. График регрессионного анализа стеноза ВСА, коэффициента ветвления и разности линейных скоростей ВСА.

ветвления от степени стеноза внутренней сонной артерии.

При точке деления 0,5 (стеноз ВСА 50%) чувствительность теста составила 74,3%, специфичность - 50%. При точке деления 0,6 (стеноз внутренней сонной артерии 60%) чувствительность составила 89%, специфичность 62%. При точке деления 0,7 (стеноз сонной артерии 70%) - чувствительность теста 94%, специфичность 23%.

Стеноз сонной артерии 60% и более является гемодинамически значимым.

ВЫВОДЫ

• 1.    Метод дуплексного сканирования с цветным картированием и мультиспиральная компьютерная ангиография позволяют выявить гемодинамический фактор и оценить его влияние на сте-нотический процесс в области бифуркации каротидных артерий.

• 2.    Стеноз каротидной артерии 60% и более свидетельствует о нарушении нормальных математических связей между геометрическими параметрами каналов и характеристиками вращательно-поступательного движения крови в них.