Основные схемы соединения трехфазных цепей
Автор: Пилипенко Е.С., Пилипенко А.С.
Журнал: Теория и практика современной науки @modern-j
Рубрика: Физика и астрономия
Статья в выпуске: 12 (30), 2017 года.
Бесплатный доступ
В статье рассмотрены основные схемы соединения трехфазных цепей.
Трехфазные цепи, расчет, постоянный ток, вольт амперная характеристика
Короткий адрес: https://sciup.org/140270611
IDR: 140270611
Текст научной статьи Основные схемы соединения трехфазных цепей
Чтобы определить схему соединения трехфазной цепи, необходимо рассмотреть способ соединения фаз приемника и обмоток генератора. Всего существует два способа соединения – треугольник и звезда. Из этого следует, что существует всего четыре возможных варианта соединения трехфазных цепей:
-
1) звезда – звезда;
-
2) треугольник – треугольник;
-
3) звезда – треугольник;
-
4) треугольник – звезда.
Первым в названии схемы ставят способ соединения обмоток генератора. Наибольшее распространение получили первый и третий способ соединения схемы, так как при таком соединении в случае нарушения симметрии фаз исключаются возможные потери энергии.
Остановимся на них более подробно.
Соединение элементов трехфазной цепи звездой.
На рисунке 3 изображена схема интересующей нас цепи. Такие схемы в основном работают при номинальном напряжении в 380В и их используют для питания силовых и осветительных приемников. В данной схеме действуют 3 линейных и 3 фазных напряжения, кроме этого протекают три фазных и три линейных тока и ток нейтрального провода. Рассмотрим эти величины более подробно.
Линейными называют токи, протекающие по линейным проводам – /А, 1В , 1С . Направление от генератора к нагрузке принимают за положительное направление линейных токов. Индексом /л обозначают линейные токи, одинаковые по модулю, без указания какого-либо дополнительного индекса.
Фазными называют токи, протекающие в фазах трехфазных приемников - 1А , 1В , 1С . Положительным направлением в данном случае считают путь от линейного провода к нейтральному. Чтобы определить значение каждого из фазных токов, применяют закон Ома. Это значение еще зависит и от общего сопротивления приемника, определяющаяся значением соответствующей фазы.
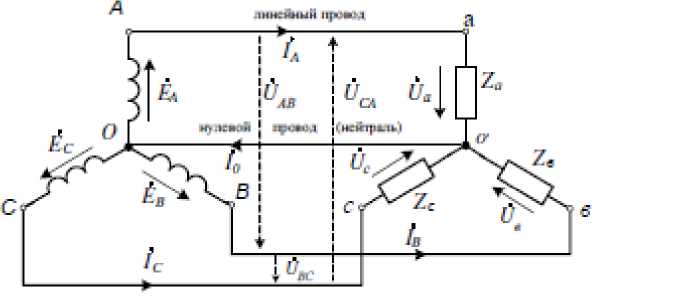
Для определения значения тока нейтрального провода используют первый закон Кирхгофа: i0 = ia + ib + ic.
Положительным считается направление тока от приемника к нагрузке.
Напряжение между началами фаз генератора называют линейным, а напряжение между концом и началом каждой фазы принято называть фазным. В фазном напряжении положительным считается направление от начала к концу каждой фазы.
В нашей схеме есть нейтральный провод, благодаря которому всю схему можно разделить на три составляющие (три замкнутых контура). Каждая схема представляет собой отдельный контур, состоящий из собственных элементов. Ток, протекающий через них, однороден, так как все элементы соединены последовательно.
Из всего вышесказанного следует, что линейные токи равны соответствующим фазным токам. in = i ^ .
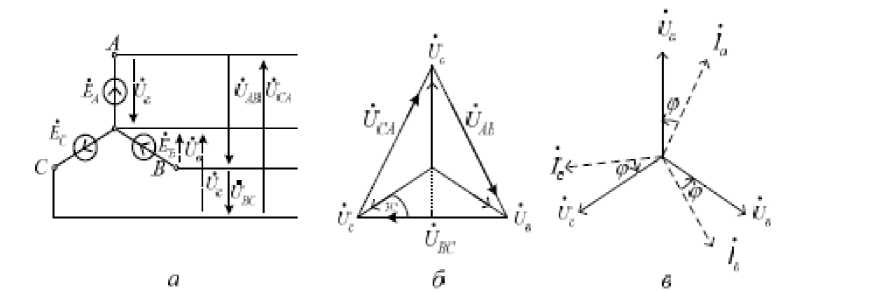
Фазы приемника и соответствующие им обмотки генератора соединены параллельно, следовательно, йа = ЁА ; йв = Ё В ; йс = Ё С (3.1).
Векторная диаграмма Э.Д.С. совпадает с векторной диаграммой фазных напряжений (рисунок 3.1).
Между линейными и фазными напряжениями существует соотношение, для определения которого воспользуемся уравнениями, приведенными для схемы 7.6,а. Если принять во внимание равенство (3.1), то применив второй закон Кирхгофа, получим следующие уравнения:
й АВ =Ё а - Ёв; йвс =ЁИ- Ё С , йС А = Ё а — Ёа (3.2).
На рисунке 3.6 (б) представлена векторная диаграмма фазных и линейных напряжений соответствующая уравнению (3.1). С ее помощью легко определить количественные и фазовые соотношения в цепи с симметричным приемником.
UAB, UBC, UCA — это вектора линейных напряжений. Они опережают соответствующие им вектора фазных напряжений Ud, UB, Uc на угол — , а друг относительно друга они сдвинуты на угол —. Фазовое 6 3
значение напряжения в V3 раз меньше соответствующего ему линейному напряжению. Это видно из рисунка 3.6(б), так как й л = ^cos30°, т.е. u „ V^ (3.3).
Чтобы определить токи в каждой фазе, воспользуемся формулами:
] = ^ / = ^В /
Й с
Zc"
d 7 3 В 7 С Za zb
В симметричных приемниках токи сдвинуты по отношению к другим фазам на один и тот же угол, и они будут равны по модулю. Легко определить, что геометрическая сумма трех векторов тока равна нулю, если построить векторную диаграмму (рисунок 3.6. в): Id + 1в + 1с = 0
Из этого следует, что если приемник симметричный, то тока в нейтральном проводе нет, следовательно, необходимость в нем отпадает.
Соединение элементов трехфазной цепи треугольником.
Если фазы комплексного сопротивления приемника Х ^в , Хвс, Хса включить между линейными проводами, как показано на рисунке 3.7(а), то такое соединение называется треугольник. Равенства йав = йАВ , йвс = йвс, йса = йСА говорят нам о том, что при таком соединении фазные напряжения приемника равны линейным напряжениям генератора. . . .
иав ивс иса
Формулы /ав = —, /вс = —, /са = — (3.6), помогают вычислить ав Тав вс ^вс са Тса 4 Z токи фаз приемника в рассматриваемой нами цепи.
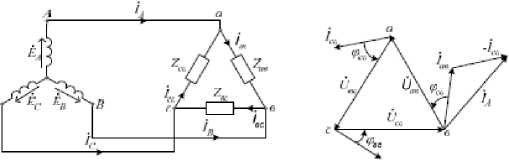
При соединении цепи треугольником, в отличие от соединения звездой, фазные токи не равны линейным. Чтобы определить линейные токи, воспользуемся первым законом Кирхгофа (схема 3.7 а): /А = /ав — ^ са , ^ В ^ вс ^ ас , ^ С ^ са ^ вс (3.7).
Если воспользоваться векторной диаграммой фазных токов (рис. 3.7 б), то с помощью полученных ранее уравнений можно определить линейные токи графически. Векторы фазный токов образуют фазную систему только в том случае, если приемник симметричный. Из схемы 3.7(б), следует, что если приемники симметричные: 1п = ^31 ф (3.8).
Отличительная черта трехпроводниковой цепи заключается в том, что независимо от характера приемников сумма линейных токов равна нулю: 1А + 1В + 1С = 0.
Список литературы Основные схемы соединения трехфазных цепей
- Иванов И.И. Электротехника. Основные положения, примеры и задачи / Иванов И.И., Лукин А.Ф. - Москва: Высшая школа, 2002 - 192 с. - ISBN: 978-5-4439-1008-6
- Каганов И.Л. Промышленная электроника. Москва: Высшая школа, 1968 - 160 с. - ISBN: 5-283-04642-7
- Калинин В.Ф. Трехфазные цепи в электрооборудовании. Тамбов: Изд-во Тамбовского государственного технического университета, 2007 - 72с. ISBN 978-5-8265-063205.


