Основы динамической корректировки коэффициентов чувствительности группы однотипных датчиков (на примере косинусного закона распределения)

Важнейшей частью современных робототехнических и человеко-машинных систем являются датчики (сенсоры) различных типов. При этом высокие требования к живучести и точности измерений в сочетании с невозможностью или затруднительностью участия человека в выполнении ремонтно-восстановительных работ в экстремальных условиях эксплуатации порождают актуальную необходимость интеллектуализации датчиков. В [1] указано, что в отличие от адаптивного датчика, обладающего свойствами автоматической настройки своих параметров в зависимости от текущих условий, интеллектуальный датчик дополнительно должен осуществлять:

– автоматическую коррекцию погрешности, появившейся в результате воздействия влияющих величин и/или старения компонентов;

– самовосстановление при возникновении единичного дефекта в датчике;

– самообучение.

Как известно, живая природа предоставляет нам примеры множественности рецепторов в составе глаза и уха. Сенсоры технических систем во многом похожи на органы зрения и слуха. Это сходство может проявляться по-разному, но в рамках темы данной статьи обратим внимание на следующие примеры применения набора одно- типных датчиков:

– акустическая система, содержащая ряд микрофонов вокруг башни, в составе боевого робота "Скорпион" [2] обеспечивает возможность моментально и весьма точно определять направление на источник звука (выстрела), чтобы соответственно направлять ствол пушки;

– измеритель мощности дозы (ИМД) [3–5], содержащий ряд сенсоров (счетчиков Гейгера) вокруг цилиндра из вольфрамового сплава, также предоставляет пользователю угол направления на источник радиационного излучения.

Характерной особенностью систем такого вида является необходимость одинаковости чувствительности датчиков. Между тем, параметры различных производимых счетчиков регистрации излучения представлены в [6]. При этом в графе "Чувствительность" указано, например: 60– 75 имп/мкР для счетчика "Гамма-7"; 285– 385 имп/мкР для счетчика "Гамма-8"; 31– 39 имп/мкР для счетчика "Гамма-10". Как видно, каждая модель допускает изначальный разброс около 25 %. В связи с этим выполняется настройка параметров программного обеспечения (коэффициентов чувствительности) в устройствах радиационного контроля прежде всего на этапе изготовления, а также и периодически на этапе эксплуатации при регламентных работах с использованием эталонного источника.

Но если мы говорим об актуальности интеллектуализации сенсорных систем, то поставим задачу динамической корректировки коэффициентов чувствительности, т. е. непосредственно в ходе рабочего функционирования, на этапе эксплуатации без эталонного источника.

Такая возможность существует и является благоприятной в той мере, в какой допускается считать, что фон, накопленный за длительное время в промежутках между ситуациями наличия источников, обладает свойством изотропности.

Актуальность совершенствования систем радиационного контроля указана, например, в [7]. При этом предполагается использование мобильных наземных, воздушных и подводных робототехнических средств. Приборы радиационного контроля могут быть установлены и стационарно в удаленных, опасных и труднодоступных местах. Во всех вариантах более предпочтительными являются интеллектуальные измерительные средства, обладающие свойством самовосстановления.

ПОСТАНОВКА ЗАДАЧИ

Считаем, что нам задана зависимость математического ожидания измеренного значения от параметров настройки датчика. Соответственно имеем возможность манипулировать смещениями. В частности, в составе программного обеспечения ИМД для каждого датчика предусмотрен коэффициент чувствительности, номинальное значение которого равно единице.

Целью статьи является получение формул, на основе которых будет обеспечена возможность вычислить величину дрейфа датчика, чтобы затем произвести пересчет его параметров настройки (коэффициента чувствительности). Для этого в программном обеспечении изделия должно быть предусмотрено формирование исходных данных следующим образом.

Проверяя отсутствие источника излучения (отсутствие чрезмерной неравномерности результатов измерений, поступающих от датчиков), выполняем накопление фона в течение очередного интервала времени (такта). Точнее говоря, правильнее учитывать, что уровень фона может меняться, поэтому каждый такт накопления фона должен завершаться, когда среднее (или медианное) значение результата накопления достигнет заданного значения. На каждом такте выполняем сортировку значений, полученных от всех датчиков. Формируем массив счетчиков B i , j — количество случаев попадания i -го датчика в j -ю позицию сортированного списка значений. Отсчет индексов производим от нуля.

Пусть M — количество тактов; N — количество счетчиков.

Очевидно, что для каждого значения i действует равенство

N - 1

M = Z B ij .

j = 0

Для каждого датчика вычисляем нормированные суммы на половине счетчиков:

N - 1

Q. = T7 Z B i , j

Mjl ’j при четном количестве N,

Q, = — iM

к личестве N.

B N - 1

2 i , ₂

N -I       к

+ Z B.j j=0

при нечетном ко-

Каждую такую сумму Q i будем называть дисбалансом. При отсутствии дрейфа (в исходном состоянии) дисбаланс равен 1/2, а при увеличении дрейфа до полной ширины статистического разброса дисбаланс становится равным 1.

Понятно, что дрейфующий датчик приобретает наибольший дисбаланс, а остальные датчики приобретают меньший (равномерно распределенный между ними) дисбаланс противоположной направленности.

БАЗОВЫЕ ФОРМУЛЫ

Дрейфу подвержены все датчики, но в интервале времени между сеансами пересчета коэффициентов чувствительности чрезмерный дрейф наиболее вероятен только у одного датчика. Поэтому в рамках данной статьи в используемой математической модели предполагается, что дрейфу подвержен только один датчик.

Обозначим p ( a , x ) — плотность вероятности распределения измеряемой величины x в области значений, ширина которой характеризуется параметром a . При этом без ограничения общности для удобства вычислений можно считать, что среднее значение равно нулю.

Обозначим L — величина дрейфа в сторону занижения. Это значит, что плотность вероятности приобретает вид p ( a , x + L ).

Обозначим также интегральную функцию вероятности распределения:

X

P ( a , X ) = j p ( a , x ) d x .              (1)

-to

Запишем вероятность попадания дрейфующего датчика в j -ю позицию сортированного списка, при этом отсчет индексов ведем от нуля:

q ( a , L , N , j ) =

(N - 1)!   x j!(N — 1 — j)!

- ( N - 1 ) ! j ! ( N - j ) !

: ,                          . XT _ ; "1^to

P ( a , x /( 1 - P ( a , x ) )        + .„ +

J-to

to x j P(a, x)j (1 - P(a,x))N 1 j p (a,x + L) dx.     (2)

-to

,      ( ^N - 1 ) !

( j - 1 ) ! ( N - j ) !

to j P(a,x)j 1 (1 - P(a,x))W j p(a,x) dx.

-to

Здесь в подынтегральном выражении первый множитель соответствует j датчикам, у которых

измеренное значение оказалось меньше, чем x ; второй множитель соответствует ( N – 1 – j ) датчи-

Получился интеграл, являющийся выражением q ( a , 0, N , j – 1). Поэтому суммирование по формуле (7) удобно выполнять в порядке убывания индекса j . Вычисляемая сумма приобретает вид

кам, у которых измеренное значение оказалось больше, чем x ; третий множитель определяет вероятность того, что дрейфующий датчик дает значение в интервале от x до x + d x . Комбинаторный коэффициент учитывает варианты перестановок всех датчиков, кроме дрейфующего.

Уместно заметить, что формула (2) определяет вероятность того, что значение от дрейфующего

n

Q ( a ,0, N ) = ^ ^ ( n - j + § ( n j = 0 .

^{- ( N - 1 ) !} _x j ! ( N - j ) !

x P ( a , x ) j ( 1 - P ( a , x ) )

IT - “I to

I N - j

- -to

.

датчика оказалось j -й порядковой статистикой. В отличие от формул, имеющихся, например, в [8] или [9], записанных для одинаковых датчиков, для варианта с дрейфующим датчиком каждый момент j -й порядковой статистики может быть записан в виде суммы трех величин (как в статье [10]). При этом (2) является одной из этих трех величин для момента порядка 0.

Обозначим серединный индекс

N при четном N:     n =--1,             (3)

Появившийся множитель ( n - j + 5 ( n ) ) является следствием объединения подобных членов. Учитывая, что P ( a , -to ) = 0 и P ( a , to ) = 1, нетрудно видеть, что в этой сумме имеется только один ненулевой член, имеющий индекс j = 0 и нижнюю границу интервала интегрирования. С учетом (3)–(6), как и следовало ожидать, получаем тождество

при нечетном N :

n =

N - 1

Обозначим серединный множитель

при четном N :      5 ( j ) = 1,               (5)

при нечетном N :   5 ( j ) = 1 при j ^ n ,

8 ( n ) = 1/2.                  ⁽⁶⁾

Поставленная цель статьи формализуется как вычисление суммы вероятностей попадания на половину позиций сортированного списка:

n

Q ( a , L , N ) = ^ 8 ( j ) q ( a , L , N , j ).        (7)

j = 0

Рассмотрим частный случай L = 0. Появилась возможность проинтегрировать формулу (2) по частям следующим образом:

q ( a ,0, N , j ) =    ⁽ N ^1)! x

⁽           ) j ! ( N - 1 - j ) !

Q ( a ,0, N ) = 2.                  (8)

Для рассмотренного случая L = 0 было несущественно, является ли область интегрирования бесконечной или ограничена отрезком.

Далее будем считать, что диапазон случайного разброса измеряемой величины ограничен интервалом [ - a , a ] . При этом формулы (2) и (7) надо переписать несколько иначе.

Заметим, что если дрейфующий датчик дает значение меньше, чем – a , то оно заведомо попадает в нулевую позицию. Такое событие возникает с вероятностью P ( a , L - a ) .

Оставшаяся часть интервала возможных значений дрейфующего датчика [ - a , a - L ] есть интервал интегрирования для формулы (2). Поэтому

( N - 1 ) !

q (a, L, N, j) = —7----—- x j!(N -1 - j)!

a - L x j P (a, x) j (1 - P (a, x ))W 'jp (a, x + L) dx,    (9)

- a

to x j P(a,x)j (1 - P(a, x))N 1 j p (a, x) dx =

-to

n

Q ( a , L , N ) = P ( a , L - a ) + ^ 5 ( j ) q ( a , L , N , j ) . (10) j = 0

Для формулы (9) выполним интегрирование по частям:

q ( a , L, N , j ) = —7---- x j ! ( N - 1 - j ) !

P ( a , x ) j ( 1 - P ( a , x ) ) N ¹ j P ( a , x + L )

- a - L

значениях индекса j . Поэтому при суммировании по формуле (10) происходит взаимное сокращение всех интегралов, кроме одного или двух интегралов (в зависимости от четности N ) с серединными индексами.

При четном N сумма интегралов превращается в один интеграл:

- a

( N - 1 ) !

( j - 1 ) ! ( N - 1 - j ) !

a-L j P(a,x)j 1 (1- P(a,x))N 1 j x

- a

x p ( a , x ) P ( a , x + L ) d x +

j ! ( N - 2 - j ) !

a-L j P(a,x)j (1-P(a,x)p 2 j

- a

I ( a , L , N ) =

_     ( N - 1 ) !

7 ^N - 1Y ^N - 1)!

x p ( a , x ) P ( a , x + L ) d x.          (11)

a - ^L          N                 N 1

x j P ( a , x ) ² ’( 1 - P ( a , x ) ) "2 p ( a , x ) P ( a , x + L ) d x . (12) - a

При j = 0 в этой формуле первый интеграл отсутствует, а при j = 1 полностью (кроме знака) совпадает со вторым интегралом, если его рассматривать при j = 0. Аналогично и при следующих

При нечетном N сумма интегралов превращается в два интеграла. При этом, учитывая (4) и (6), обнаруживаем возможность выполнить суммирование и превратить их в один интеграл:

I ( a , L , N ) =

( N - 1 ) !

2 ( n - 1 ) ! ( N - 1 - n ) !

a - L j P (a, x) n 1 (1 - P (a, x))' 1 n p (a, x) P (a, x + L) dx +

- a

2 n ! ( N - 2 - n )

a - L j P(a, x)n (1 - P(a,x))    n p (a,x)P (a, x + L) dx =

- a

( N - 1 ) !

^a _^L              N - 1 j                       N ^{- 1} 1

j P ( a , x ) ²    ( 1 - P ( a , x ) ) ²    p ( a , x ) P ( a , x + L ) d x .

- a

В формуле (11) выполняем подстановку преде-

лов интегрирования:

n

zb( j)

j = 0 .

(N -1)!   X j!(N -1 - j)!

x P ( a , x ) j ( 1 - P ( a , x ) ) ^N1 j P ( a , x + L ) = D ( a , L , N ) - P ( a , L - a ) .

Здесь обозначена сумма

- a - L

—I - a

Формула (10) приобретает вид

Q ( a , L , N ) = D ( a , L , N ) + 1 ( a , L , N ) .     (14)

Нетрудно убедиться, что, в частности:

D ( a ,0, N ) = 0;    D ( a , a , N ) = 1;

D ( a ,2 a , N ) = 1; I ( a ,2 a , N ) = 0;

( N - 1 ) !

j ! ( N - 1 - j ) !

x P ( a , a - L ) j ( 1 - P ( a , a - L ) ) N 1 j

Учитывая (8) и (14), можно записать еще одно то ждество: I (a,0, N) = “ •

Эти тождества могут быть полезными при проверке правильности программирования.

КОСИНУСНОЕ РАСПРЕДЕЛЕНИЕ

На практике обычно мы имеем дело с нормальным распределением случайных значений, полу-

чаемых от датчиков. Как известно, к нормальному распределению близко и распределение Пуассона, которому подчиняются данные от счетчиков регистрации радиоактивного излучения. Однако здесь мы рассмотрим косинусное распределение случайных значений и найдем его параметры, при котором оно имеет максимальное сходство с нормальным распределением. В отличие от экспоненциальной функции Лапласа косинусная функция допускает аналитическое вычисление интеграла (12). Точнее говоря, далее мы увидим, что получающийся результат имеет вид суммы, вычисление которой является не самой сложной задачей с точки зрения программирования.

Определим функцию плотности вероятности косинусного распределения в следующем виде:

I x I

1+ X cos I п — I p (a, X, x) =------2a2 a .           (15)

Для сравнения с нормальным распределением далее нам потребуются известные формулы, которые здесь мы запишем в следующих обозначениях:

g ( o ^x ) =

exp oV 2 n

-

L 2 o 2 ) ,

G ( ^o , ^x ) = 2 | ^{1 +} erf

L

o

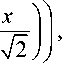
2x erf (x) = —j= f exp (-1 ) dt.

СХОДСТВО КОСИНУСНОГО РАСПРЕДЕЛЕНИЯ С НОРМАЛЬНЫМ РАСПРЕДЕЛЕНИЕМ ПО КРИТЕРИЯМ ДИСПЕРСИИ И ЭКСЦЕССА

Амплитудный параметр, предназначенный для регулирования остроты функции распределения, имеет диапазон

0 1.                   (16)

Полученная функция коэффициента эксцесса (18) имеет точку максимума.

Чтобы найти ее координаты, надо вычислить производную по параметру X и приравнять нулю. Нетрудно получить решение:

Интегральная функция плотности вероятности:

X

E max

п ² ( 15 - п ² ) 15 ( п² - 6 )

= 0.872354,

P ( a , X , x ) =

E max

Применяя формулы интегрирования, известные, например, из [11, c. 89] или [12], нетрудно получить момент второго порядка (дисперсию) косинусного распределения

15 ( п ² - 6 ) п ² ( 7 п ² - 60 )

- 3 = - 0.495661.

I x I _a 1 + X cos I п I

2 f-------^L— a Z x ²dx

0        2 a

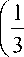
2 X

a

и момент четвертого порядка

a 1 + X cos I п x I

2 f------^L—— x ⁴d x = a⁴

0       2 a

I ¹ -X

L 5 п

Как видно, полученное значение амплитудного коэффициента (21) оказалось в границах диапазона (16), предназначенного для регулирования остроты функции плотности вероятности распределения. Соответствующее максимальное значение коэффициента эксцесса (22) наиболее близко подходит к уровню "ноль". Это значит, что острота косинусного распределения в этом случае наиболее близка к остроте нормального распределения.

В дополнение к требованию сходства коэффициентов эксцесса предлагается приравнять дисперсии. При этом нетрудно получить следующее соотношение:

В соответствии с определением, указанным, например, в [13, с. 18], получаем коэффициент эксцесса

a = о

15 ( п ² - 6 )

7 п ² - 60

= 2.527337 о .

- — 4X ( п ² - 6 )

E ( ^X ) = 5---- v— 3.              (18)

- — 2X I

L ³       )

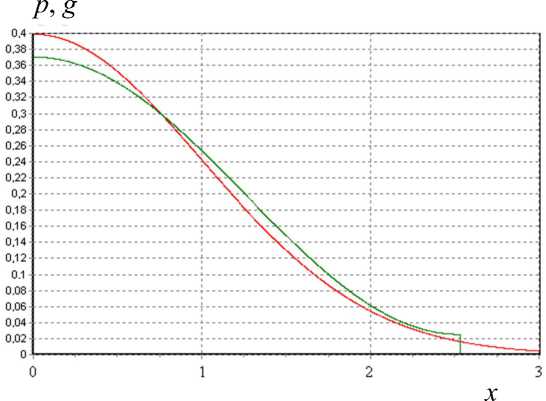
На рис. 1 представлены график функции (19) с параметром о = 1 и график функции (15) с параметрами (21) и (23). Как видно, этот критерий сходства, основанный на близости интегральных статистических характеристик, пытается увеличить урезанный "хвост" за счет уменьшения вершины.

a

J

Рис. 1. Сравнение косинусного распределения p с нормальным распределением g по критерию близости дисперсии и эксцесса

Преобразование уравнения (24)

По известным правилам вычисления производной от интеграла получаем

f x

1 + X cos I n —

I a

2 a

—1= exp I c\2nV

f x cos I n —

V a

Преобразуем к виду двух отдельных интегралов:

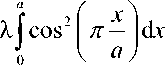
a 2

aV2 f x |    ( x 1, exp - cos n   dx.

cV n ₀ V 2 c J V a J

КРИТЕРИЙ РАВНОМЕРНОГО СХОДСТВА КОСИНУСНОГО РАСПРЕДЕЛЕНИЯ

С НОРМАЛЬНЫМ РАСПРЕДЕЛЕНИЕМ

Формулирование критерия равномерного сходства

Рассмотрим также критерий равномерного сходства функций, а именно выполним минимизацию интеграла от квадрата их разности:

a

Интеграл в левой части можно взять по известной формуле [11, с. 90], получается a /2.

Интеграл в правой части рассматриваем как функцию, вычисляемую численным интегрированием.

Обозначим:

a u =—1= , c V2

H ( z ) = J exp ( - zt ² ) cos ( n t ) d t .

Уравнение (24) приобретает вид:

CO

+ J ( g ( c , X ) ) d x .

a

Эти интегралы допускают перегруппировку, в которой только один из двух интегралов играет роль для задачи минимизации:

Преобразование уравнения (25)

d F ( a , X , c )

a

F ( a , X , c ) = J p ( a , X , x ) ( p ( a , X , x ) - 2 g ( c , x ) ) d x +

O

d a a + 2 J 0

= p ( a , X , a ) ( p ( a , X , a ) - 2 g ( c , a ) ) +

^dp ⁽d a^ ’ x ) ( p ( a , X , x ) - g ( c , x ) ) d x = 0 ^;

Составим систему двух уравнений относитель но параметров a, X :

dF(a , X , c)

(-^^ = 0,             (24)

d F(a , X , c)

—  = 0.                (25)

d a

a

2J

1 + X cos I n —

2 a

. x . x

a V a 2 a

exp

^“

f x

1 + X cos I n —

V a

2 a ²

I a 1 + А cos I п

к

+

к

a

—

—

к

г

2 a

г

exp

—

к

a

ctV 2 п

exp

a ²

a

I х 1 + А cos I п

к

—

к

2 ст ²

У

—

к

a

—

г

2ст ²

У

= 0.

Во втором уравнении содержится левая часть

первого уравнения (26), которая равна нулю, по-

этому имеется возможность упрощения:

a

I х 1 + А cos I п

к

2 a

ст к2 п

exp

x ²

—

к

2 ст ²

У

X

x

ХАп — sin

a

a

1.1 I х 1 + Х cos I п —

=1

a

a

—

2 a

dx -J

ctV 2 п

exp

—

к

х2 L dx

2 ст ² J

—

a

—

к

X

+

2 a

ctV 2 п

exp

x ²

+

ctV 2 п

exp

—

к

—

к

2 ст ²

X

У

a

2 ст ²

.

Здесь просматривается

"хвост"

нормального

распределения, который выходит за границу коси-

нусного распределения, поэтому выполняем даль-

„ _ х . I _х Ап -ysin I п —

a

a

—

a

к

нейшее упрощение:

a

d r +

a

1.1 I х 1 + Х cos I п —

к

к

г

4 a ²

—

exp

У

a

—

—

к

2 a

г

a

к

2 ст ²

= 0.

Преобразуем к виду трех отдельных интегра-

лов:

Оставшийся интеграл возьмем по частям:

I х 1 + Х cos I п —

—А

a

—

стЧ^п

exp

x ²

—

к

2 ст ²

У

X

1 х . I х \ хАп —sin I п — I d x =

a

a

г

к

г

a

^+А 1

a

2 a

exp

—

к

= 1 — G ( ст , a )

x ²

2 ст ²

—

+

ctV 2 п

exp

—

к

a

2 ст ²

.

к

x

х cos I п —

a

a

+

У

I х 1 + А cos I п

a

—

г

к

г

^+А 1

к

2 a

ctV 2 п

exp

x ²

—

к

2 ст ²

I х 1 , cos I п — I d x +

a

У

1      ■ I х

Ап sin I п —

—

2 a

a

+

x

г

к

= 1 — G ( ст , a )

—

к

ст ³

2 π

exp

x ²

—

к

2 ст ²

г

+

ст ^2п

exp

—

к

х cos I п ^х I d x =

a

У

a ²

2 ст ²

.

Первый из двух оставшихся интегралов кратен левой части первого уравнения (26), поэтому он равен нулю. Член с квадратной скобкой конкретизируем, освободим от скобки и перенесем в правую часть уравнения:

a

XJ

।       . ( x

X^sin I к к a

—

2 a ²

x

+ 3 „^ex P

г

—

к

x ²

к

I x L x cos I к — I dx = к aJ

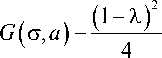
( 1 — X ) a

+ -—exp oV 2 к

—_a_ I к 2o2J

— X a

^{1 — X} . 2 a

o V2 K

exp

(   „' II k—2? 1

В правой части приводим подобные члены:

a

XJ

( .     . ( x

XKSin I к к a

1    X ²   1 _r( a I

= —+--- erf — 1= +

4  8  2 кo V2 J

a exp o V2t

— a_ j к 2 o ² )"

—

2 a ²

+

x exp o V2k

— x_ I к 2 o ^{2 J}

к

Воспользуемся обозначением (27), а также обозначим функцию, вычисляемую численным интегрированием:

= 1 — G ( o , a ) —

x x cos

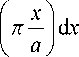
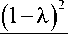
a o V2T

exp

a ²

X

—

к

2 o ²

J

X ( 1 — X )

T ( z ) = J exp ( — zt ² ) cos ( K t ) 1 ²d t .

Уравнение (25) приобретает вид квадратного уравнения

В левой части интеграл разбиваем на два интеграла и применяем формулу синуса двойного угла, в правой части приводим подобные члены:

X ² —X ¹ 6 u ³ T ( u ² ) + π

X o ³ V2 K

a

J exp

(

к

2 o ²

—

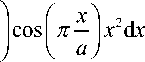
+ 2 — 4erf ( u ) + uy= exp ( — u ² ) = 0.   (29)

π

2 a X к r 4 0 2"^J

■ Io x I a sin I 2к— Ixdx = к a J

Решение системы двух уравнений

Путем программирования получено следующее решение системы двух уравнений (28) и (29):

3 X ² z z a

' .   G ^{( o} , ^{a ) +}     ^ ^ex p

4  4           ov 2 т

— a__ j к 2 o ²J"

X = 0.857, u = 1.671;

a = 2.363 o .

По формуле, известной из [11, с. 84], получаем

2 a

^{X к} Г * Io ^x 1

—- sin 2 к— x d x =

4 a ^{2 J}0     к a J

X ²

Вычисленный интеграл переносим в правую часть и приводим подобные члены:

X a³ o ³ V2 T

J ^ex P

( a2 J „ ft2 cos (Kt) 12d t = к 2o2 J

На рис. 2 представлены график функции нормального распределения (19) с параметром o = 1 и график функции косинусного распределения (15) с параметрами (30) и (31). Как видно, рассмотренный критерий обеспечивает весьма близкое сходство.

ФОРМУЛЫ ВЫЧИСЛЕНИЯ ФУНКЦИИ ДИСБАЛАНСА ДЛЯ КОСИНУСНОГО РАСПРЕДЕЛЕНИЯ

Интеграл (12) для (14) после подстановки (15) и (17) приобретает вид:

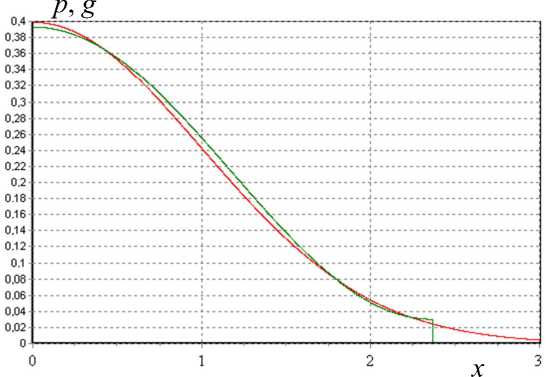
Рис. 2. Сравнение косинусного распределения p с нормальным распределением g по критерию равномерного сходства

. X

+ t + z +— sin π

(n( t+z))

= 1 + z + t ( 1 - cos ( n z ) ) +

(    X . z x)     z x X

+ I t +— sin ( n t ) I cos ( n z )+— cos ( n t ) sin ( n z ) .

V   n J         n

Это позволяет нам записать требуемый интеграл в следующем виде:

iU n A = (

^{( ,} )     n ! 2 2 ^N

- cos ( n z ) ) V +

X         A

+ cos ( n z ) R + —sin ( n z ) S I . n        J

Здесь обозначены:

1 - z

I ( a , L , N ) =

( N - 1 ) !

N - 1¥ N -dl 2 JI 2 J

1-z       г3

Т Т     Г 1   IX

U =    1 -I t + —sin

-1 V   V

2 ⁿ

J

1 - z

V = j ¹ -I t ⁺

-

1 V

X .

sin

π

n

A ² 1

( n t ) I     ( 1 + X cos ( n t ) ) t d t ,

J

J

a - L

Xj

- a

n

.    , x a . I n x )

a + x + X—sin I    I

______n__a

I        (^WП a - x-X—sin I I

______n__a

1 - z

^R = J ¹

2 ⁿ

—

X

2 a

2 a

-

1 V

V                    J

VJ

J

,X           A

I— sin ( n t ) I d t , n       J

( nx )               a . ( n

1 + X cos I — I a + x + L + X— sin I —( x + L ) V a J           n V a

2 a                2 a

1 - z

^S = J ^1-I t ^{+ —}

2 ⁿ

X

-

¹ V

J

Обозначим z = L / a ; t = x / a и перепишем предшествующее выражение в этих обозначениях (заметим, что, как и коэффициент эксцесса, функция дисбаланса зависит только от формы функции плотности вероятности, но не от ее ширины):

x ( 1 + X cos ( n t ) ) cos ( n t ) d t .

Из этих четырех интегралов два интеграла можно взять легко:

I ( ^ , N ) =

( N - 1 ) !

2 N n !² 2 ^N

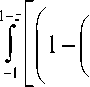
. . X .

t +— sin π

A2 A

^{( n t )} I

^L J

U = ^.(—1)- c^k k t 0 2 k + 1 ⁿ

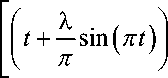
1 - z

- 1

R = у ⁽ 1 ) C^k k :02 k + 2 ⁿ

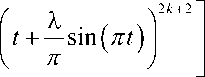
( X

1 + t + z +— sin ( п ( t + z

d t .

Для двух других интегралов применяем способ "по частям":

Выполним разложение синуса суммы и сформируем член, совпадающий с членом, имеющимся в основании степени подынтегрального выражения:

n

V = Z k=0

^{( - 1 ) k} C k 2 k + 1 ⁿ

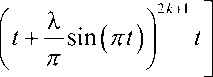
-z

n

k = 0

^{( - 1 ) k} C k 2 k + 1 "

. . X .

t + — sin

π

\ 2 k + 1

^{( n t} ) )

d t ;

s = У 1-1)1 C k [ ^2 k + 1 "

+ П 1^M

72 k + 1

X         Y k + 1

t + —sin ( n t ) I    cos ( n t )

П       )

- 1- z

1 - z (    X           A ^{2 k + 1}

C n f I t +— sin ( n t ) I sin ( n t ) d t .

- 1' V     ^{n           J}

Далее существует возможность в подынтегральных выражениях тоже выполнить биномиальное разложение, а затем для каждого получившегося произведения степеней от t и sin применить следующие формулы, известные из [14, с. 197, 198]:

Q

z

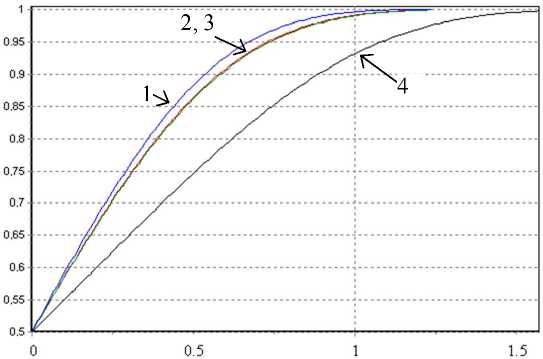
Рис. 3. Линии дисбаланса для косинусного распределения.

N = 8; линии 1 для λ = 1, 2 — λ = 0.857, 3 — λ = 0.872, 4 — λ = 0

f x" sin² m ax d x =

( 2 m ) !     x " ^{+ 1}

m ! m ! 2 2 ^m ( " + 1 )

( - 1 ) ^m m -i       .    ( 2 m ) !

+ , , У (-1) —7--- —— [x " cos((2 m - 2 k\ax\ d x ;

22m-1 ^( ) k!(2m - k)!        (( f x" sin2m+1 ax dx =

(-1) ^m ™ (-1) ^k (2 m + 1)!

)-() x " sin((2 m - 2 k + 1) ax\ d x ;

22m t0k!(2m +1 -k)!         (

"                       "! x"-k    < x sin(ax)dx = -Xt—тг;^k+TcosI ax + ^T I;

k=0 (" - k)! a       V

n f x" cos (ax) dx = Z k=0

" !     x " ^{- k}

( n - k ) ! a^{k + 1}

. <    . knA sin ax +     .

V 2 )

При нулевой степени переменной t требуется вычислять интеграл от степени синуса. В этом случае применяем известную формулу из [12], обеспечивающую понижение степени синуса в подынтегральном выражении:

f sin" (cx) dx = sin "-1(cx ) cos ( cx ) "-1 ,    -2

—                      +       sin     cx x .

ncn

Формула справедлива при n > 0.

РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЯ ФУНКЦИИ ДИСБАЛАНСА ДЛЯ КОСИНУСНОГО

РАСПРЕДЕЛЕНИЯ

На рис. 3 представлены графики функции дисбаланса для косинусного распределения при N = 8:

Q – Q контр

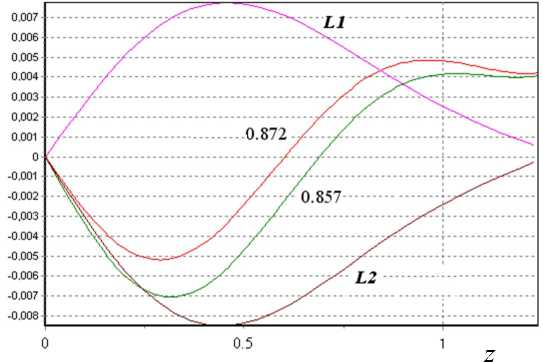
Рис. 4. Линии дисбаланса относительно контрольной линии (нормальное распределение с a = 2.44σ).

N = 8; L1 — соотношение (23); L2 — соотношение (31)

• -    верхняя линия 1 для X = 1 ;

• –    средняя линия является слиянием двух близких линий 2 и 3 для X = 0.857 и X = 0.872 ;

• -    нижняя линия 4 для X = 0 .

Точность приближения дисбаланса для косинусного распределения к дисбалансу для нормального распределения целесообразно проанализировать на основе численного интегрирования формулы (2) с подстановкой формул (19) и (20). Сначала функция дисбаланса для нормального распределения была построена в двух вариантах горизонтального масштабирования:

– линия L1 по соотношению (23),

– линия L2 по соотношению (31).

Оказалось, что L1 проходит выше обеих линий дисбаланса для косинусного распределения; L2 проходит ниже обеих линий дисбаланса для косинусного распределения.

Поэтому уместно взять усредненное соотношение a = 2.44 о , при котором в качестве контрольной построена линия дисбаланса для нормального распределения. На рис. 4 представлены построенные линии дисбаланса относительно контрольной при N = 8.

ВЫВОДЫ

На практике, выполняя корректировку коэффициента чувствительности, целесообразно соблюдать некоторую постепенность, а не полностью брать величину, вычисленную с использованием математической модели, для которой имеется ряд допущений (достоверность контроля изотропности фона; единственность датчика, подверженного дрейфу; соответствие нормальному распределению). Поэтому правомерно сделать следующие выводы.

• 1.    Представленные формулы и результаты вычислений дают зависимость дисбаланса от величины дрейфа одного измерителя в качестве основы для динамической корректировки коэффициентов чувствительности однотипных датчиков.

• 2.    Полученные две линии дисбаланса для косинусного распределения вполне приемлемы в качестве приближений к линии дисбаланса для нормального распределения.