Основы гидравлического расчета навесных вентилируемых фасадов

Suspended facade system with ventilated air gap it is a special case of walling ventilated air gap. Flow of air is free-convection in vertical ventilated channel. Convection - one of the most economical and practical method of removing moisture from the air gap.

The question is, what should be the size (width) of the gap,which providing maximum air flow pass?

We reviewed version of the definition an optimal hydraulic hinged ventilated channel for buildings in this article.

Вентилируемый фасад - это конструкция, состоящая из материалов облицовки (плит или листовых материалов) и подоблицовочной системы, которая крепится к стене так, чтобы между облицовкой и стеной образовалась вентилируемая воздушная прослойка.

Система вентилируемого фасада состоит из несущего каркаса, утеплителя и облицовочных панелей.

Навесные фасадные системы с вентилируемым воздушным зазором являются частным случаем ограждающих конструкций с вентилируемыми воздушными прослойками, которые защищают утеплитель, примыкающий к стене здания, от воздействия окружающей среды, при этом наличие конвективных движений способствует выносу влаги в атмосферу и поддержанию утеплителя в состоянии с малой влажностью [10]. Такая конструкция лишена многих недостатков, характерных для фасадов, выполненных с использованием «мокрых» технологий, и широко применяется как при ремонте, так и при возведении новых зданий.

Течение воздуха в вертикальном вентилируемом канале – свободно-конвективное или термогравитационное. Свободная конвекция – один из наиболее экономичных и практичных методов удаления влаги из воздушного зазора. Если температура поверхности выше температуры окружающей среды, то воздух, омывающий поверхность, нагревается и, становясь более легким, начинает всплывать. В этом случае плотные соседние слои воздуха заменяют поднявшийся слой. Этот принцип замещения слоев используется при проектировании воздушных прослоек [1].

Для прогнозирования влажностного режима таких конструкций необходимо иметь четкое представление картины течения воздуха в вентилируемом канале и учитывать гидравлические параметры свободно-конвективного течения воздуха в зазоре [2].

Большой вклад в изучение характеристик свободноконвективных течений (СКТ) внесли российские и зарубежные исследователи. Определению теплофизических свойств вентилируемых воздушных прослоек и их влиянию на температурно-влажностный режим ограждающих конструкций посвящены работы Михеева М. А., Эккерта Э. Р., Гершуни Г. З., Соковишина Ю. А., Мартыненко О. Г., Идельчика Е. И., Шифринсона В. Л., Жуховицкого Е. М., Остроумова Г. А., Чумакова Ю. С., Колешко С. Б., Мачинского В. Д., Фокина К. Ф., Уонга Х., Богословского В. Н., Табунщикова Ю. А., Гагарина В. Г., Козлова В. В., Цыкановского Е. Ю. и многих других специалистов [11 - 22].

В вентилируемых каналах, образованных двумя вертикальными поверхностями, свободноконвективное течение возникает при условии, что одна из поверхностей будет нагрета или охлаждена. Движущая сила, обусловленная разностью статических давлений между поступающим в канал воздухом и покидающими его, называется естественной тягой.

Результаты исследований представляют большой интерес, но для практического применения полученных результатов требуется сформулировать общий подход для определения оптимального расстояния от экрана до стены в вертикальных щелевых каналах.

Целью настоящей работы является нахождение гидравлически оптимального вентилируемого канала.

Пусть существует вертикальная щель, образованная двумя плоскостями y=0, y=h , высотой L , имеющими температуру холодной стенки Tc и температуру горячей стенки Th (см. рисунок 1). В этом пространстве, за счет сил плавучести, индуцируется вязкая термогравитационная конвекция воздуха, обеспечивающая создание теплоизолирующей воздушной завесы и подсушивание плоскостей y=0, y=h .

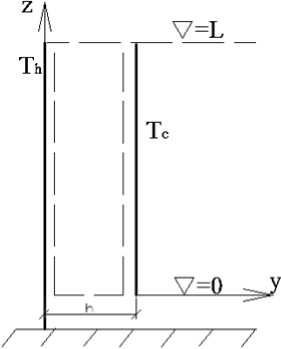
Рисунок 1. Схема вертикального канала

Свободно-конвективное течение воздуха создает восходящий воздушный поток, в котором роль «насоса» играет распределенный по высоте тепловой поток, передаваемый от плоскости y=h к воздуху. Интенсивность передачи теплоты описывается дифференциальным уравнением теплопередачи [7]:

— = Sh (Th - T)+Sc (T, - T) dz

Где S h , S c – безразмерные коэффициенты теплопередачи (числа подобия Стентона),

S = -^a

P C p v

,

v –средняя скорость воздушного потока.

Средняя скорость воздушного потока вычисляется так:

gL 1

v = Ф / л--

n

k

,

где ф =

1 + 2 - + У Z h ^j

• ^{( j )}     - коэффициент скорости для канала [3], где λ – коэффициент гидравлического

трения (число Дарси).

Для существования свободно-конвективного течения в вертикальных плоских каналах должно соблюдаться условие баротропности для двух состояний воздуха: адиабатного равновесия воздуха в канале и свободно-конвективного течения, обусловленного нагревом воздуха от горячей стенки канала.

• 1.    Получается, что при значении n=k, воздух находится в состоянии равновесия, т.е. в адиабатной щели свободно-конвективное течение отсутствует. Значит, если считать движение баротропным и заменить условие теплообмена (дифференциальное уравнение энергии) голономным условием баротропности [5], то v=0, n=k (где v - скорость течения воздуха в канале; n-показатель политропы; k-показатель адиабаты);

• 2.    Расширение воздуха в свободно-конвективном течении происходит при n

Таким образом, обобщая сказанное, можно утверждать, что если равновесному состоянию воздуха в вертикальном канале отвечает показатель политропы n = n 1 >  0 , то при всяком значении 0 <  n <  n 1 существует свободно-конвективное течение.

Расширение воздуха в свободно-конвективном течении изображается траекторией (политропой)

p на плоскости переменных ю = Ll , п = — (рисунок 2)

р p0 ,

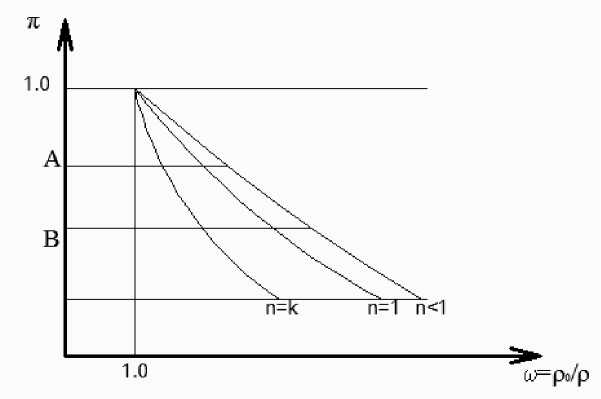
Рисунок 2. Политропное расширение воздуха в свободно-конвективном течении

Площадь между осью ω=0 и траекторией изображает «механическую работу» расширения.

Если n=k, то работа недостаточна для перемещения (подъема) воздуха в вертикальном канале и превращается в потенциальную энергию покоящегося столба воздуха.

Если n

Если 1, то расширение воздуха при свободно-конвективном течении сопровождается его охлаждением, как, например, при движении в печной трубе (подвод теплоты от топочного пространства недостаточен для расширения с увеличением температуры по длине дымохода).

Если 0, подвод теплоты обеспечивает монотонный рост температуры воздуха по длине канала. Такая ситуация характерна для обогреваемых каналов, например, для вентилируемых каналов систем навесных вентилируемых фасадов.

Интенсивность теплообмена и показатель политропы n связаны тождеством [4]:

¹       __ z f ^L ^

n =              , z := e 0, ■    ^,

1 + R dT ’ h ( ’ hJ

gh _d^__z^_

С учетом (1) равенство (3) можно так записать: 1

n =---n----------------------

1 +   (Sh T - T)+Sc (Tc - T))

gh

В силу (2), (3), (4):

gL I R dT к -1

Ф —--+--

RTc gh d _z_   k

v = ^gLrJR(Sh(Th -T) + Sc(Tc -T))+ k-1

RT gh                     k

c

Из формул (5), (6) выясняется влияние интенсивности теплопередачи и температурных напоров на среднюю скорость течения в вертикальном щелевом канале НВФ.

Возникает следующий вопрос. Пусть известны предельные температуры, вертикальный размер канала, интенсивность передачи теплоты, коэффициент скорости ф. Спрашивается, каков должен быть размер (ширина) щели, обеспечивающий пропуск максимального расхода воздуха q=hv? Такая экстремальная задача приводит к понятию канала гидравлически оптимальной ширины. Именно, вертикальный щелевой канал называется гидравлически оптимальным в том и только в том случае, если, при заданных значениях L, Sh, Sc, Tc, Th, T0, он обеспечивает пропуск максимального массового расхода воздуха в условиях свободно-конвективного течения и баротропного течения воздуха.

Тогда, как доказано в [4] и [8], показатель политропы n удовлетворяет тождеству:

11 к -1

--—--- n Л к op

1   1 RT c ---—-- nop k gL где Л := gL , где Л - приведенная длина.

RT

c

В этом случае, силу (2) и (7), в вертикальном щелевом канале устанавливается средняя скорость течения [9]:

v — ф

gL RTc RTc gL

.

^{1 —}ф gL

(gL )2

RT c

Понятие об оптимальном канале позволяет получить оценку для калибра гидравлически длинного щелевого канала. Эта оценка выглядит так:

h I Л (T - T a )

— =3— —---——

L \ gL T pC v о v c p /

В эту оценку входят коэффициенты теплопередачи ah и гидравлического трения X, сами зависящие от параметров потока в НВФ. Для размеров оптимальных щелей выполняется, в силу (10) условие подобия:

h₁      h₂

³L²1    ³L²2

, позволяющее пересчитывать, например, размеры с модели на натуру.

Естественно, полученные оценки занижены, т.к. при расчете сопротивления вертикального щелевого канала НВФ не учитываются местные потери напора (на вход, на выход, потери на крепежных кронштейнах и пр.).

Установлено, что чем короче канал, тем больше должна быть величина теплового потока, прогревающего воздух и создающего вертикальную тягу и, наоборот, в длинном канале тяга создается при меньшем тепловом потоке и, соответственно, при меньшем отклонении показателя политропы от равновесного значения ne.

Известно, что для существования СКТ необходимо разность плотностей воздуха в начальном и в конечном сечениях вертикального канала. Эта разность плотностей создает подъемную силу (тягу), перемещающую частицы воздуха вдоль вертикального канала. На входе в канал интенсивность передачи теплоты велика (за счет перепада температуры между потоком и горячей стенкой), показатель политропы мал, а градиент средней скорости максимален [6].

По высоте канала поток прогревается, вследствие чего плотность воздуха понижается, а средняя скорость растет и пульсации затухают, что характерно для конфузорного течения.

При прогреве потока n→k и вблизи выходного сечения канала градиент средней скорости уменьшается. К выходу из канала возникает некая диффузорность за счет потерь напора на резкое расширение.

Для того чтобы минимизировать потери напора на расширение потока в выходном сечении канала, нам необходимо чтобы средняя скорость СКТ была постоянной V=const, тогда в этом случае h будет расти. Вообще говоря, с точки зрения минимизации потерь (увеличения ϕ - коэффициента скорости) необходимо иметь навесной вентилируемый фасад с вентилируемой щелью, расширяющейся снизу вверх.