Основы проектирования систем виброзащиты с упругими элементами из материала МР

Самарский государственный аэрокосмический университет

Определены параметры широко применяемого в виброзащите материала МР (модуль жесткости, коэффициент Пуассона, коэффициент рассеивания энергии, коэффициент трения) в различных направлениях. На основе этих зависимостей получен метод проектирования виброзащитной системы с виброизоляторами из МР.

Виброизоляторы из материала МР (МР – “Металлическая резина” – получается холодным прессованием проволочной спирали) широко используются в виброзащитных системах [1, 2, 4]. Они имеют высокую прочность, высокий коэффициент рассеивания энергии, способны работать в условиях высокой и низкой температуры, в агрессивной среде, вакууме, радиации и так далее. Однако свойства материала МР нелинейно зависят от многих параметров: относительной

ρMR плотности материала ρ = ρ (где ρ – плот- ность материала проволоки, ρMR – абсолютная плотность материала МР), амплитуды деформации A, предварительной статической деформации Q. Применяемые модели материала МР (их обзор присутствует в [2]) в большинстве случаев основаны на рассмотрении контактного взаимодействия проволок в МР, очень сложны и малопригодны для практического применения при проектировании виброизоляторов. В настоящей работе предлагается подход к проектированию систем виброзащиты, использующих материал МР, на основе представления о МР как анизотропной сплошной среде. Такой подход также открывает возможность применения конечно-элементных программ при расчете виброизоляторов из материала МР.

Определение параметров МР

Исследовались образцы в виде куба со стороной l=25 мм, изготовленные из проволоки диаметром 0,1 мм. В принятой системе координат направление прессования – ось Х. Зависимость напряжения прессования от от- носительной плотности материала можно представить уравнением

σ press ≈ 576 ρ ^1.7              (1).

Для осуществления деформации сдвига и растяжения образцы приклеивались к жестким поверхностям. Есть некоторые отличия в деформации приклеенных и неприк-леенных образцов.

Коэффициент Пуассона

Коэффициент ν_yx (описывает влияние силы, приложенной в направлении X , на де-

ε_y формацию в направлении Y ; ν yx = -   )

εx очень мал. В рабочем диапазоне (ε ≤ 0.16) ν ≤ 0.03 . Есть зависимость от относитель-yx ной деформации

ν ≈ 0.2 ε   .            (2)

yx          x

Аналогично ν_zx . Поскольку коэффициент Пуассона в данном направлении очень мал, не имеет значения, приклеены или свободны нагрузочные поверхности образца.

При сжатии в направлении Y в направлениях X и Z наблюдаются значительные петли гистерезиса (рис. 1).

Они приблизительно подобны петле в направлении Y . Если перестроить петли в координаты ε_y - ε_x (или, соответственно, ε_y - ε_z ), результат можно описать приблизительно в виде ε_x ≈ - aε_y ± b , где коэффициент a играет роль коэффициента Пуассона, а коэффициент b является остаточной деформацией. Знак + относится к процессу нагрузки, знак – к процессу разгрузки.

Коэффициент Пуассона и остаточная деформация при свободных нагрузочных по-

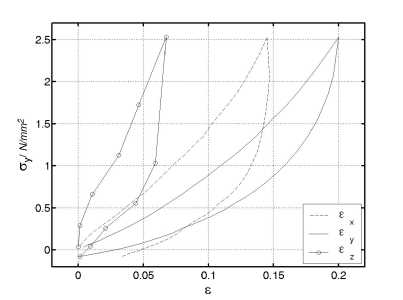
Рис. 1. Петли гистерезиса в направлениях X и Z при сжатии в направлении Y (приклеенный образец)

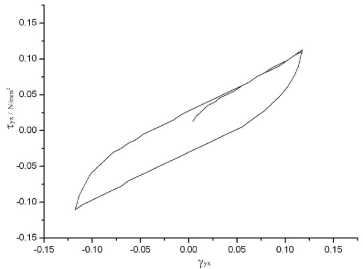
Рис. 2. Деформация образца из МР в одном из направлений сдвига

верхностях зависят от амплитуды деформации и относительной плотности материала.

£ x « ( - 17 s y ± 3.1s y )s y p .      (3)

Аналогично ν_xz .

s - « ( - 8.5 s y ± 0.46 s y ) s y p .     (4)

Аналогично ν_xz .

У приклеенных образцов нагрузочные поверхности деформироваться не могут, поэтому деформация свободных поверхностей больше, и, соответственно, коэффициент Пуассона больше.

Для приклеенных нагрузочных поверхностей вид зависимостей несколько отличается.

sx «-0.66sy ± (-0.075p + 0.03 5), (5) то есть коэффициент Пуассона vxy « 0.66. Аналогично νxz . Точно так же sz «-0.3sy ± (-0.033p + 0.014),     (6)

то есть коэффициент Пуассона v_zy « 0.3 . Аналогично ν_yz .

При растяжении (экспериментально проверено до _s « - 0.05) деформация материала МР в боковых направлениях не изменяется, следовательно, коэффициент Пуассона равен 0.

Модуль сдвига G и сила трения при сдвиге

Петля гистерезиса при сдвиге (кроме ее концов) близка к линейной (рис. 2), поэтому ее можно приблизительно описать уравнением т = GY ± Tf,            (7)

где τ_f – напряжение от сил трения.

Из обработки большого количества измерений (для различной относительной плотности и различного диаметра проволоки) получены соотношения

Gyx: Gxy : G-y «1:1.53:2.75(8)

THyx:Thx,, :THZy «1:1.26:1.99;(9)

G -x = G yx ; G x- = G xy ; G yz = G zy ;

THzx = THyx ; THxz = THxy ; THyz = THzy

Первый индекс – направление действия силы, второй – направление, в котором материал закреплен при сдвиге.

Зависимость от относительной плотности

G yx « 6.65 p МРа , T Hyx « 0.107 p¹'¹ МРа. (11)

Модуль сдвига и напряжение от сил трения в других направлениях можно получить, используя зависимости (8), (9) и (10).

Интересно, что в относительных координатах

G yx

G yx

σ press

6.65 ρ ^1.7

576 ρ ^1.7

= ^0.0115 , (12)

то есть все модули сдвига зависят только от силы прессования, причем линейно.

Модуль упругости (модуль Юнга) и напряжение трения при сжатии и растяжении

Упругая линия петли гистерезиса на сжатие и растяжение существенно нелинейна. Целесообразно описать петлю как сумму напряжения на упругой линии σ_L и напряжения трения σ_H .

с т = c L ± o_H . (13)

Упругая линия и напряжение трения могут быть определены по экспериментально процессам нагрузки σ ₁ и разгрузки σ ₂ по уравнениям

C 1 + c 2 C 1 — c 2

^c L = —2— и ^c H = —2— соответственно в диапазоне деформаций [0.7 A _min;0.7 A _max] [3]. Для направления Х этот диапазон составил s_x g [ - 0.06;0.24], в направлениях Y и Z s g [ - 0.06; 0.16]. Линии c_L

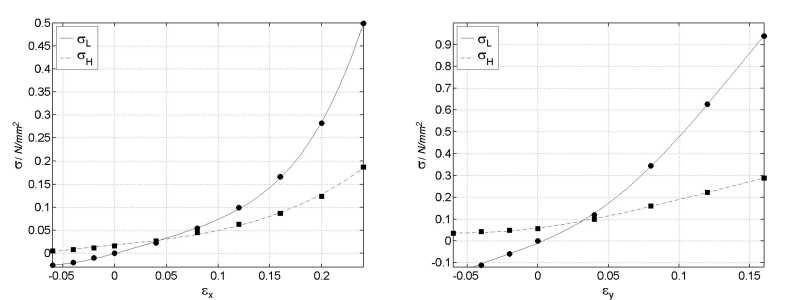
Рис. 3. Упругая линия и напряжение трения петли гистерезиса образца материала с р = 0.18 в направлениях Х и Y

и o H для относительной плотности р = 0.18 в направлениях Х и Y приведены на рис. 3.

Зависимость напряжения трения от ε удовлетворительно описывается полиномом степени 3, зависимость от ρ в направлении Х сходная с зависимостью при сдвиге (прямая пропорциональность), в направлениях Y и Z зависимость более сильная (пропорционально ρ ^1.7 ).

он 2 (0.0181 + 0.231г + 0.0691г2 + Hx                         xx

+ 7.71г3)Г Р1

x ( 0.18 )

o_Hy 2 (0.0597 + 0.819 г y + 6.51 г y -

1.7

— 16.8г3)Г Р1

y ( 0.18 J

Аналогично σ_Hz

Зависимость упругой линии от ε удовлетворительно описывается полиномом степени 4, зависимость от ρ в направлении Х сходна с σ_press (пропорционально ρ ^1.7 ), в направлениях Y и Z зависимость более сильная (пропорционально ρ ² ).

o Lx 2 (0.613 + 1.771 г_х - 20.4 г 2 +

+ 160г>, fр |            <|6> x x ( 0.18 J oLy 2(2.69 + 14.2гy + 139гy -

— 632 г 3 ) г f P 1            (17)

y ^y ( 0.18 J

Аналогично σ_Lz .

Первый сомножитель в этих произведениях аналогичен модулю упругости E .

Коэффициент рассеивания энергии в различных направлениях

Уравнения (7) – (11) и (13) – (17) дают возможность построить приблизительно петли гистерезиса (с вертикальными начальными участками нагрузки и разгрузки) и оценить коэффициент рассеивания энергии ψ . В направлении Y жесткость материала МР существенно больше, чем в направлении Х, а различие силы трения не так велико, поэтому коэффициент рассеивания энергии в направлении Х существенно больше. Например, для амлитуды деформации _г = 0.1 и относительной плотности р = 0.18 получаем

— 2 1.4. С увеличением р сила трения в на-ψy правлении Y растет несколько быстрее, и различие уменьшается, но все равно при р = 0.3

получаем ^ ^ « 1.2.

ψ y

При сдвиге петля гистерезиса близка к линейной, ее площадь пропорциональна 2τγ , а потенциальная энергия деформирования пропорциональна 2 Gγ . Поэтому коэффи- цτиент рассеивания энергии пропорционален , и из уравнений (8) и (9) следует V yx : Vxy : Wzy ~ 1: 0.82 : 0.72 , а из уравнений (11) следует, что ψ при сдвиге пропорционален (р)“°-6.

Значения ψ_x и ψ _yx сопоставимы. При

ψyx г = y = 0.1 отношение —^12 1.12, при ψx

ψyx г = y = 0.15 отношение---2 0.82 .

ψ x

Коэффициент трения

Поскольку значительная доля энергии рассеивается в виброизоляторе не при трении внутри материала МР, а при трении материала МР о стальные детали конструкции виброизолятора, необходимо знать коэффициент трения МР по стали f. Для этого обра- зец прижимался известной силой P1 и смещался силой P2 в перпендикулярном направлении. Относительная плотность ρ и направление силы (P1 в направлении прессования Х, P2 в перпендикулярном направлении Y, и наоборот) на коэффициент трения не влияют. Обнаружена слабая зависимость f от напряжPения прижатия. При малых значениях с = jy коэффициент трения f=0.1, далее он слабо растет и после с* 0.75MPa остается постоянным и равным 0,125.

Проектированиевиброзащитной системы

Рассмотрим пример проектирования виб-розащитной системы на основе полученных зависимостей для параметров материала МР. Пусть виброизолятор работает на сжатие в направлении Х или Y . Даны: масса защищаемого объекта m , требуемая резонансная частота виброзащитной системы f ₀ , амплитуда действующего ускорения a , допустимое ускорение защищаемого объекта на резонансе w ₀ .

По этим данным можно, используя приближенную линейную модель, найти необходимую динамическую жесткость виброизолятора kd = 4п2 f02 m,(18)

необходимый коэффициент передачи на ре- зонансе

w

П ° = "7’(19)

амплитуду деформации вaиброизолятора на резонансе

w ₀

A = ^

и требуемый коэффициент рассеивания энергии 2 π

V * — η ₀

.

Для обеспечения большого времени работы виброизолятора желательно, чтобы его относительная деформация не превышала 10%. Примем 8 ° = 0.1. Тогда высота упругого элемента из МР _A

H = ₈ •           (22)

Минимальная предв0арительная стати- ческая деформация Q определяется весом защищаемого объекта. Однако она может быть увеличена при помощи дополнительного сжатия упругих элементов из материала

МР. Получаем

mg ^ C l ( 8 q ), F

Q где 8q _ H , g _ 9.81 m /52, F - площадь поперечного сечения виброизолятора.

Таким образом, виброизолятор совершает колебания между точками с относительной деформацией

Q + A

8 _ —---■ 8

1 _H ; 2

_ Q - A

H

.

Тогда динамическая жесткость виброизолятора kd *

^C L ^{( 8} 1 ) ^{+ C} H ^{( 8} 1 ) - ( ^C L ⁸ 2 ) - ^C H ⁸ 2 ) p

F

2 A

( A l + s_H ) р

2 A

где

AL = CL (81) - CL (82) ;

5H _ CH (81) + CH (82) .

Подставив в (25) уравнения (18) и (20), получаем

2w°m _ (Al + 5h )F

Площадь петли гистерезиса (предполагая, что участки первоначальной нагрузки и разгрузки – вертикальные линии) приблизительно равна

A W ' * 2 AF(c_H (8 1 ) + c_H ( 8 ₂)) _ 2 AFs_H .

Поскольку реальные участки нагрузки и разгрузки криволинейны, это завышенная оценка площади петли. Используя подобие петель виброизоляторов из МР, установленное в [4], и приведенную там же линию нагрузки (или разгрузки) в обобщенных координатах, можно считать, что площадь реальной петли гистерезиса

A W * 0.75 A W' * 1.5 AFs„ .

H

Максимальная потенциальная энергия деформирования из-за несимметрии петли будет различна для нагрузки и разгрузки, поэтому для ее расчета принято среднее значение

W * ^0.2 5 ^{(( c} l ^{( 8} 1 ) ^{+ C} h ^{( 8} 1 ) ^{- C} L ^{( 8} 0 )) ⁺

^{+ ( C} L ^{( 8} 0 ) - ^C L ^{( 8} 2 ) ^{+ C} H ^{( 8} 2 ))) AF ^_    .

_ 0.25( A _L + s_H ) AF

Тогда коэффициент рассеивания энергии

A W    6 s_H

ш =--«---—

W   A l + s- •

Из (25)    A l + s -

2 Ak_d F

Тогда

ψ

3 Fs H Ak d ^.

С учетом (18) – (21), получаем

2 πma

Fs„ _----

H 3

.

Разделив почленно (28) на (29), получим

A L + sH _ 3w0

sH     πa

.

Получаем следующий алгоритм проектирования виброизолятора:

• 1.    Рассчитать значения A и H по уравнениям (20) и (22).

• 2.    Принять некоторое значение ρ (для обеспечения минимального веса виброизоля-

• 3.    Принимая ряд значений Q, получать по уравнениям (24) значения ε ₁ и ε ₂ , по уравнениям (14) и (16) (или по уравнениям (15) и (17) для направления, перпендикулярного направлению прессования) значения σ_H ( ε ₁), σ_H ( ε ₂) , σ_L ( ε ₁) , σ_L ( ε ₂) , по уравнениям (26) и (27) значения A L и s_H , добиваться выполнения условия (30).

• 4.    Если условие (30) выполнено, при помощи уравнения (29) найти значение F .

• 5.    Проверить выполнение условия (23). Желательно также, чтобы е ₂ >  0, иначе необходимо приклеивать материал МР к опорным поверхностям, обеспечивая работу материала на растяжение.

• 6.    Если при принятом значении ρ условия (30) или (23) не выполняются ни при каком Q , увеличить значение ρ и повторить пункты 3, 4, 5. На практике p <  0.35 , и виброизолятор с такой плотностью обычно уже является чрезмерно жестким. Если изменение значения ρ не дало результата, требования к виброизолятору невыполнимы.

тора можно начинать с наименьших технологически достижимых значений, например, p _ 0.18 . При небольших требованиях к прочности виброизоляторавозможно p _ 0.15 .

Полученный алгоритм легко реализовать в виде программы для компьютера. В результате получаем высоту H и площадь сечения F виброизолятора, его относительную плотность ρ и необходимую предварительную деформацию упругого элемента Q . Этого достаточно для изготовления виброизолятора.

Проектирование виброизолятора, работающего на сдвиг, ведется аналогичным образом, с использованием уравнений (7) – (11).