Основы решения задач с параметрами для подготовки абитуриентов к ЕГЭ по математике

Задачи с параметрами, давно вошедшие в практику вступительных испытаний в вузы и ЕГЭ по математике, принадлежат к числу задач, наиболее трудных для абитуриентов, как в логическом, так и техническом плане. В этих задачах выбор метода, процесс решения, запись ответа предполагают определенный уровень знаний школьника, позволяющий анализировать, сравнивать и обобщать полученные результаты.

Рассмотрены и проанализированы основные виды уравнений с параметрами. К ним относятся: линейные и квадратные уравнения, дробно-рациональные уравнения с параметром, сводящиеся к линейным, иррациональные, тригонометрические, показательные и логарифмические уравнения с параметрами.

Исследуются методы решения данных уравнений. А именно: аналитический метод, функциональный подход, графические методы для координатной плоскости (Х; У) и координатной плоскости (Х; А).

Различные подходы к решению уравнений с параметрами

Чтобы определить алгоритм решения задачи с параметром, необходимо задать себе простой вопрос: как бы решалась задача, если бы вместо параметра стояло конкретное число. При этом не следует забывать, что параметр, в действительности являясь числом, может принимать любые значения. Иными словами, уравнение с параметром является фактически семейством уравнений, рассматриваемых при фиксированном значении параметра. При разных значениях параметра приходится использовать различные методы, применяемые при решении уравнений и неравенств с постоянными коэффициентами. Поэтому основной принцип аналитического решения задач с параметрами заключается в разбиении области изменения параметра на такие участки, что на каждом из них получается уравнение или неравенство, которое можно решить одним и тем же методом. На вступительных экзаменах и ЕГЭ по математике чаще всего встречаются два типа задач с параметрами:

• 1)    для всех допустимых значений параметра найти множество всех решений уравнения или неравенства;

• 2)    найти все значения параметра, при каждом из которых выполняются заданные условия.

Ответы в задачах этих двух типов различаются по существу: в ответах к задачам первого типа перечисляются все возможные значения параметра, для каждого из которых записываются полученные решения; в ответах к задачам второго типа перечисляются все значения параметра, для которых выполнены условия задачи.

Во многих задачах требуется определить значения параметров, при которых заданная функция удовлетворяет определенным условиям. Это задачи с параметрами, в которых ставятся вопросы, касающиеся областей определения и значений функций, промежутков возрастания и убывания, точек максимума (минимума), наибольших и наименьших значений. При решении задач такого типа целесообразно исследовать функцию, используя ее производную. Подобные задания были представлены в блоке «С» вариантов ЕГЭ по математике. Предложенные задачи классифицированы в зависимости от того, какое свойство функции является основным в решении [1].

При изменении параметра меняются функции, входящие в уравнение или неравенство, а в соответствии с этим меняются и различные характеристики этих функций, влияющие на множество решений. Удобным средством для изучения таких изменений, облегчающим анализ и решение задачи, являются те или иные графические интерпретации. Можно выделить два основных приема, используемых в задачах с параметрами:

• 1)    построение на плоскости (Х; У) семейства кривых, зависящих от параметра a ;

• 2)    построение графического образа задачи на плоскости «параметр -неизвестная», например, на плоскости (Х; А ).

Первый подход часто оказывается удобным в задачах с двумя неизвестными x и у и одним параметром. Второй обычно применяется в задачах, в которых фигурируют лишь неизвестная x и параметр.

• Пр имер 1. Найти все значения параметра b , при которых

  уравнение

  
  

• 4 sin x — 7 = b ( 1 + ctg ² x ) имеет хотя бы одно решение.

Аналитическое решение:

При sin X ^ 0 , т.е. X ^ ПП,   n G Z , данное уравнение равносильно

уравнению: 4 sin3 x — 7 sin2 x = b.

Пусть sin x = p ^ —1 < p < 1 и p ^ 0.

Тогда 4 p ³ — 7 p ² = b . Построим схематично график функции:

y(p) = 4p3 — 7p2 при p ^[—1;0)u(0;1];

y'(p) = 12p2 —14p ;

y (p) = 0 О 12p —14p = 0; или 2p(6p — 7) = 0; откуда pY = 0; p2 = -.

И p, и p, e[— 1;.0)u(0;1] (рис. 1).

Рис.1. Интервалы монотонности и экстремума функции y(p)

Исследуем функцию   y ( p ) в граничных точках области определения

y(p) = —1; y(1) = —3.

При p ^ 0; y ( p ) ^ 0.

Из рисунка 2 видно, что график функции y ( p ) пересекается с семейством прямых y = b , хотя бы в одной точке, при b G [ — 1; 0 ) .

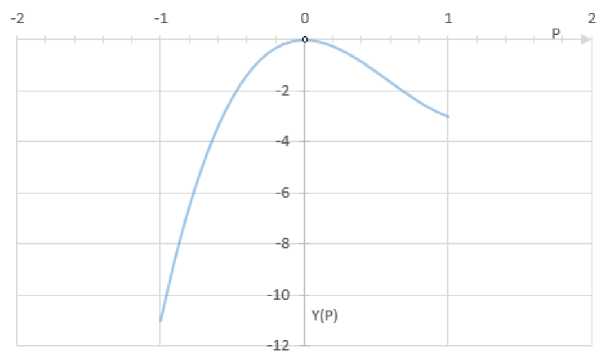
Рис. 2 График функции y (p ) = 4 p - 7 p

Пример №2

При каких значениях параметра p уравнение

log3 (23 - x2 - 2 x - 3| )= logi 3 + log2 (69 - 3 p)

имеет 3 различных корня.

Решение:

Аналитическое.

ОДЗ: . 23 -I'

x ²

—

2x - 3| > 0

69 - 3p > 0

'|x2 - 2x - 3| < 23

3p < 69

⇒

- 23 <  x ² - 2 x - 3 <  23

p <  23

x2 - 2x - 26 < 0

^ U² - 2 x + 20 >  0

⇒

p <  23

x g (1 - V27J1 + V27);p < 23.

В области допустимых значений функции данное уравнение равносильно:

23-| x ² - x 2 - 3| =

69 - 3 p

^ | x ² - 2 x - 3| = p ^

x2 - 2 x - 3 = p

^x2 - 2 x - 3 > 0

x2 - 2 x - 3 = - p x2 - 2 x - 3 < 0

Для того чтобы исходное уравнение имело три решения, уравнение первой системы должно иметь два решения, а уравнение второй системы – одно решение, или наоборот. Значит в одной из систем дискриминант больше нуля, а в другой дискриминант равен нулю.

Г D_x = 4 - 4( - 3 - p ) >  0

( p + 4 >  0

^ 1       ^ p = 4.

[ p = 4

| D₂ = 4 - 4( - 3 + p ) = 0

D i = p + 4 = 0 ^

D 2 = p - 4 = 0^

2) Графическое

Построим график функции (рис. 3) y_t ( x ) = x²

- 2 x - 3| и семейство прямых

y ₂( x ) = p : x ² - 2 x - 3 = 0 ^ x 1 =- 1; x ₂ = 3; _x =₊ 2 = 1 ; y (1) = 1 - 2 - 3 = - 4 0 ₂

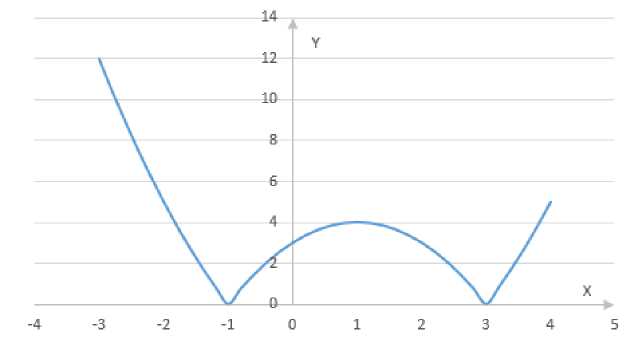
Рис. 3. График функции (рис. 3)

y , ( x ) = | x ² - 2 x - 3|

Практическая отработка получаемых знаний и навыков

Задачи с параметрами являются сложными потому, что не существует единого алгоритма их решения. Спецификой подобных задач является то, что наряду с неизвестными величинами в них фигурируют параметры, численные значения которых не указаны конкретно, но считаются известными и заданными на некотором числовом множестве. При этом значения параметров существенно влияют на логический и технический ход решения задачи и форму ответа.

По статистике многие из выпускников не приступают к решению задач с параметрами на ЕГЭ. По данным ФИПИ всего 10% выпускников приступают к решению таких задач, и процент их верного решения невысок: 2-3%, поэтому приобретение навыков решения трудных, нестандартных заданий, в том числе задач с параметрами, учащимися школ по-прежнему остается актуальным [2].

Возможность и умение решать задачи с параметрами демонстрируют владение методами решения уравнений и неравенств, осмысленное понимание теоретических сведений, уровень логического мышления, стимулируют познавательную деятельность. Для развития этих навыков необходимы большие усилия со стороны педагогов по созданию подобных заданий и контролю за их выполнением, что приводит к введению дополнительных курсов в школе, дополнительным материальным затратам. Успешному изучению методов решения задач с параметрами при достаточно небольших затратах времени со стороны педагога могут помочь современные информационные технологии, которые в настоящее время так привлекают школьников. Обучение при их использовании становится более увлекательным, живым, востребованным [3].

В частности, в подготовке к ЕГЭ могут помочь специализированные интеллектуальные программные комплексы, которые позволят облегчить работу педагога, поскольку обладают способностью генерировать различные задания на основе базовых, а также обеспечат не только контроль за выполнением заданий, но и своевременную корректировку и подсказку на определенном этапе ее решения. В качестве системы для отработки навыков решения задач с параметрами и закрепления материала можно использовать интеллектуальную систему Math-Bridge, являющуюся узкоспециализированной интеллектуальной средой разработки учебных объектов для математических и инженерных дисциплин, разработанной Немецким исследовательским центром по искусственному интеллекту (Deutsches Forschungszentrum für Künstliche Intelligenz-DFKI). Интеллектуальный редактор учебных объектов позволяет создавать объекты различной конфигурации в зависимости от их целей и назначения, которые способствуют отработке полученных теоретических знаний на практике. Возможности редактора математических формул очень широки: предусмотрена вставка специальных символов (букв греческого алфавита, знаков принадлежности множеству и др.), кроме того существуют шаблоны, которые позволяют с легкостью составлять такие элементы как обыкновенные дроби, матрицы, системы уравнений и другие [4-5].

Упражнение, позволяющее отработать навык решения параметрических уравнений, должно содержать как минимум три типа компонентов: в первом будет содержаться описание задачи, второй объект будет отображать реакцию системы при правильном ответе, третий – сообщит студенту о том, что его решение было неверным. Соединяя между собой эти объекты, мы можем сделать содержимое упражнения динамическим и адаптивным. В результате формируется ориентированный граф, отображающий структуру рассматриваемого упражнения (рис. 4).

Здесь блоки Task содержат постановку задачи. Блоки Interaction представляют собой компоненты для взаимодействия с обучающимся (ввод ответа, выбор одного ответа из нескольких). Блоки Сorrect и Wrong содержат в себе реакцию системы на ответ обучающегося [6]. В блоках Hint находятся подсказки – необходимый для выполнения конкретного задания теоретический материал. Как видно из рисунка, если обучающийся вводит верный ответ, система оповещает его об этом и происходит переход к следующему блоку с заданием. В случае неверного ответа, система предлагает повторить некоторый теоретический материал и попробовать ответить еще раз.

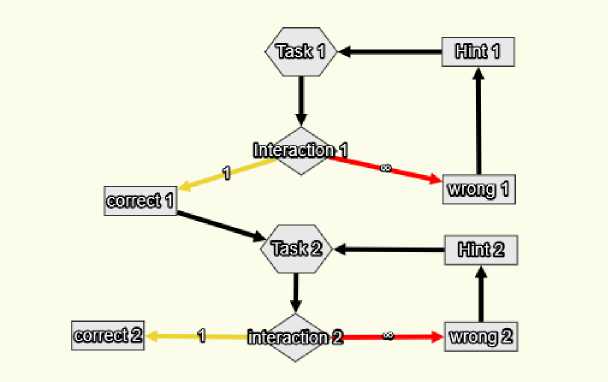
Рис. 4. Ориентированный граф

Интерфейс для обучающегося, начинающего выполнение задачи, выглядит следующим образом (рис. 5)

При каких значениях параметра р уравнение log, (23 - |х2 - 2х - 3|) = log, 3 + log, (69 - Зр)

I имеет 3 различных корня.

Область допустимых знамений

• □    х е (1 - V27?l + V27);/Т < 23

о хе (1-V27:1 + >Ш\р >23

• □    хе (-1;3); р < 23□    х е (-1;3); р > 23

• Р ис. 5. Рабочее окно системы Math-Bridge с условием задачи

В случае неверного ответа, предлагается помощь в виде одного из способов решения параметрических задач на определенном шаге. Она появляется в том же окне, что позволяет обучающемуся не тратить время на поиск необходимых теоретических сведений, а быстро освежить в памяти те или иные моменты и продолжить выполнение упражнения (рис. 6).

X с (-1;3); р > 23

Неверно1

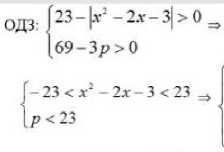
Пх2 -2х-3|<23 [Зр < 69 х2 - 2х - 26 < О х!-2х+20>0 ~ ^<23

х е (1 JlTA + V27); р < 23

Рис. 6. Рабочее окно системы Math-Bridge с неправильным ответом и подсказкой

Таких подсказок может быть несколько, так же, как и задач, разнообразие которых обеспечит сама система. Когда обучающийся ответит верно, система оповещает его об этом следующим образом (рис. 7), после чего система предложит следующее задание.

Рис. 7. Рабочее окно системы Math-Bridge с правильным ответом

Заключение

В настоящее время существует большое количество математических пакетов программ, которые могут быть использованы в качестве инструмента отработки навыков у учащихся при подготовке к ЕГЭ, но далеко не все они предоставляют возможности, связанные с тонкой настройкой инструментария обучения.

Учитывая тот факт, что задачи с параметрами могут быть рассмотрены в множестве комплексных чисел, интеллектуальная программа Math-Bridge позволит произвести настройку и расширить круг рассматриваемых задач с параметрами, что обеспечит более углубленное изучение математики как самостоятельно, так и при использовании ее на факультативных курсах, поскольку комплексные числа не входят в программу школьного курса математики [7-8]. Результаты исследования показывают, что привлечение информационных технологий в дополнение к традиционному обучению позволят повысить успеваемость, облегчить работу педагога, повысить интерес к знаниям, расширить банк заданий для отработки навыков решения задач с параметрами. Предложенный подход может быть использован для подготовки учащихся 10-11 классов общеобразовательных средних школ, а также выпускников техникумов к ЕГЭ по математике. Предлагаемый материал ориентирован не только на получение навыков решения типичных задач с параметрами, но и на повышение уровня их математической культуры, развития логики мышления и тем самым на подготовку к ЕГЭ.