Основы теории расчета электропневмомеханического оборудования для анализа ДНК

В настоящее время объектами научных и диагностических исследований медико-биологических лабораторий всего мира все чаще становятся нуклеиновые кислоты — ДНК и РНК. Сегодня в ходе исследований ставятся задачи, не только требующие определить наличие исследуемой нуклеиновой кислоты в образце, но и определить ее исходное количество и нуклеотидную последовательность — сиквенс. Наиболее доступным, достоверным и высокочувствительным методом, позволяющим обнаружить ДНК в пробе и оценить ее количество, является метод полимеразной цепной реакции (ПЦР).

Разработка в 1983 г. сотрудником фирмы "Сetus", США, Кэри Мюллисом метода полимеразной цепной реакции (Polimerase chain reaction — PCR) является одним из крупнейших методологических открытий в современной молекулярной биологии, за что он в дальнейшем был удостоен Нобелевской премии. Принцип метода полимеразной цепной реакции широко используется как в научных исследованиях, так и в практическом здравоохранении и службе госсанэпидемнадзора при генотипировании и диагностике инфекционных заболеваний [1].

Полимеразная цепная реакция — это циклически повторяющаяся температурозависимая ферментативная реакция, в ходе которой происходит экспоненциальный рост количества специфического фрагмента исходной двухцепочечной ДНК. При этом реакционная смесь содержит короткие синтезированные фрагменты одноцепочечной ДНК — праймеры, способные связываться с молекулами ДНК в определенной последовательности, специфичной для исследуемого объекта.

Как видно из рис. 1, каждый цикл реакции состоит из трех этапов.

• 1)    Денатурация исходной двухцепочечной

ДНК (разведение спиралей).

• 2)    Связывание праймеров с комплементарными участками исследуемой последовательности (при их наличии) при температуре, определяемой длиной и структурой праймеров.

• 3)    Достраивание двухцепочечной структуры на заданном участке при определенной температуре.

При этом количество исходных копий фрагментов ДНК увеличивается в экспоненциальной зависимости в каждом цикле (амплификация). Математически реакция описывается следующей формулой

Kn = Kо • 2 n, где Kn — количество фрагмента ДНК, получаемого в ходе реакции, K0 — исходное количество фрагмента ДНК, n — число циклов реакции.

На рис. 2 приведен пример процесса изменения температуры реакционной смеси, при которой протекает полимеразная цепная реакция. Количество полученного продукта зависит как от числа циклов n , так и от числа копий K ₀ исходной ДНК.

Теоретически из одной копии ДНК может быть получено любое количество продукта (до исчерпания праймера) и, как следствие, реакция практически не имеет ограничений по чувствительности. Это и определяет ПЦР как высокочувствительный метод, способный обнаружить единичные копии ДНК.

К разработке оборудования для реализации ПЦР приступили практически одновременно с открытием самой реакции. Фактически для успешного протекания полимеразной цепной реакции необходимо устройство, в котором можно обеспечить изменение температуры реакционной смеси по заданному закону и с определенной степенью точности. Наиболее распространенное название приборов данного класса — ДНК-амплификаторы.

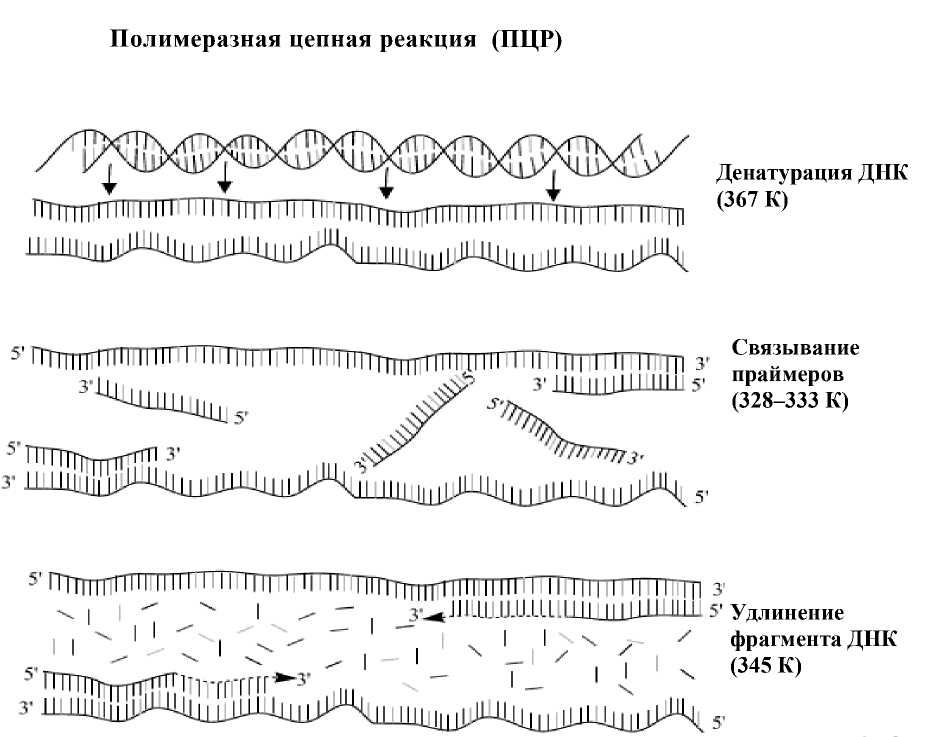
Рис. 1. Протекание полимеразной цепной реакции

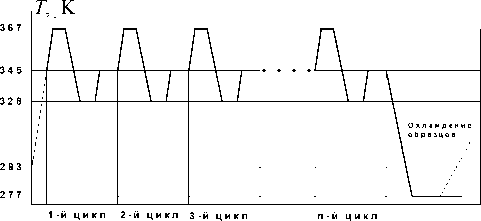
Рис. 2. Пример процесса изменения температуры, необходимого для обеспечения протекания полиме-

разной цепной реакции

предприятия, как Techne (Великобритания), Ер-pendorf (Германия) и др. Активно разрабатывалось оборудование и в России. Прежде всего — это разработки Института биологического приборостроения РАН, ООО "НПФ СТМ-Ц", МГТУ им. Н.Э. Баумана, ООО "Компания Биоком" и АО "ДНК технология". За прошедшие годы разработкой и производством амплификаторов ДНК занимались десятки фирм в промышленно развитых странах. Сегодня созданы и серийно выпускаются амплификаторы ДНК, обладающие различными техническими характеристиками, отличающиеся принципом действия и предназначенные для работы в различных условиях.

Одним из первых серийно выпускаемых амплификаторов был прибор фирмы Perkin Elmer (США) — DNA Thermal Cycler 480. Практически др    рр   ру

КОНСТРУКТИВНАЯ СХЕМА АМПЛИФИКАТОРА

Разработчики амплификаторов особое внимание наряду с увеличением вместимости лока в котором размещаются микропробирки с образцами реакционной смеси, уделяют обеспечению максимально высокой скорости изменения температуры и, что очень важно, однородности температурного поля.

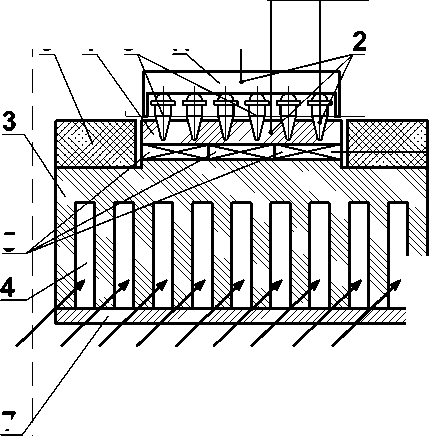
Наиболее широкое распространение получила схема амплификатора ДНК, принцип действия которой основан на использовании в качестве источника тепла термоэлектрических модулей (ТЭМО). Конструктивная схема такого устройства приведена на рис. 3. В данном устройстве термоэлектрические модули применены для нагрева и охлаждения пластины-держателя 1, в которой размещаются микропробирки с реакционной смесью 8. Характер процесса (нагрев или охлаждение) зависит от полярности включения тока [2]. Устройство состоит из блока нагрева/охлаждения и системы управления. В состав блока нагрева/охлаждения входят: пластина-держатель 1 для размещения микропробирок 8, датчики температуры 2, радиатор 3, батарея ТЭМО 5, ограничитель потока воздуха 7, теплоизоляция 6 и нагреваемая крышка 17.

Система управления состоит из предварительного усилителя 9, АЦП 10, микропроцессорного устройства 11, ЦАП 12, усилителя тока 13, импульсного источника тока 14, устройства ввода/вывода информации 15 и внешней ЭВМ 16 с программным обеспечением для сбора и обработки информации.

При включении тока, обеспечивающего нагрев пластины-держателя 1 с размещенными в ней микропробирками 8, происходит охлаждение радиатора 3. При изменении полярности включения тока на батарее термоэлектрических модулей происходит отвод тепла (охлаждение) от пластины 1 и нагрев радиатора 3. Поскольку этот процесс циклический, для повышения точности регулирования температуры пластины 1 необходимо стабилизировать температуру радиатора 3. С этой целью в состав блока включено устройство охлаждения, обеспечивающее постоянную продувку каналов охлаждения 4 радиатора 3 потоком воздуха.

8 17

Поток воздуха

Блок

нагрева / охлаждения

Система управления

Рис. 3. Принципиальная схема прецизионного программируемого устройства на-грева/охлаждения.

1 — пластина-держатель, 2 — датчики температуры, 3 — радиатор, 4 — воздушные каналы, 5 — термоэлектрические модули, 6 — теплоизоляция, 7 — ограничитель потока воздуха, 8 — микропробирки, 9 — предварительный усилитель, 10 — АЦП, 11 — микропроцессорное устройство, 12 — ЦАП, 13 — усилитель тока, 14 — источник тока, 15 — устройство ввода/вывода информации, 16 — внешняя ЭВМ, 17 — нагреваемая крышка

Во избежание испарения реакцио время нагрева и ее конденсации на ропробирок 8, в состав устройства греваемая крышка, температура ко живается в диапазоне 381–388 К.

Как отмечено выше, одной из ва при создании данных устройств яв чение однородности теплового пол при максимальной скорости ее нагр ния по циклу: нагрев от 323 К до дующим охлаждением до 323 К. П ряется 35–40 раз и затем пластина ными в ней микропробирками о 275–277 К.

ПОСТАНОВКА ЗАДАЧ

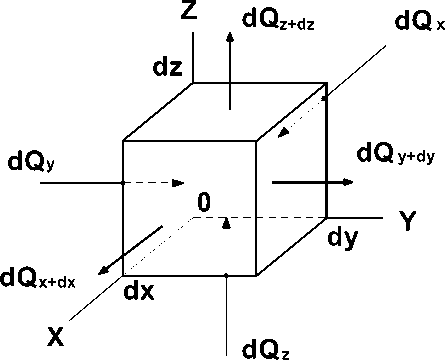
Рис. 4. Элементарный объем. К математической модели теплового состояния

Успешное решение задачи обеспечения однородности теплового поля, высокой скорости на-грева/охлаждения пластины и высокой стабильности амплификатора ДНК во многом зависит от результатов теоретических исследований теплового состояния устройства, которое определяется нестационарными тепловыми источниками (стоками), процессами конвективного теплопереноса и теплофизическими и электрическими свойствами материалов. Исследование теплового состояния в данной постановке сводится к решению нестационарной сопряженной трехмерной нелинейной задачи.

Математическая модель

Для описания теплового состояния блока на-грева/охлаждения амплификатора необходимо совместное решение трехмерного нестационарного уравнения теплопроводности и уравнения энергии для потока воздуха в каналах охлаждения радиатора.

Приступая к составлению трехмерного нестационарного уравнения теплопроводности, принимаем, что элементы устройства, подлежащие расчету, выполнены из материалов с изотропными свойствами, а их температурные деформации пренебрежимо малы по сравнению с линейными размерами.

Рассмотрим элементарный объем со сторонами d x , d y и d z , для которого, используя закон теплопроводности Фурье, определим количество теплоты, накопленной за интервал времени d τ . Если к граням d x d z , d x d y и d y d z элементарного объема (рис. 4) подвести тепло

dT dQY = -X — dx • dz • dT , dy dT dQz = -X — dy • dx • dT , dz '

то с противоположных поверхностей будет отводиться тепло d Q X +d X , d Q Y +d Y и d Q Z +d Z соответственно. Применив ряд Тейлора для разложения неизвестных функций, получим:

dQX+dX = dQX + - (dQX )dx + •••, dx dQY+dY = dQY + T"(dQY )dy + ••• , dy dQz+dZ = dQz +|-(dQz )dz + ••• dz

В разложениях оставляем по два первых члена. Таким образом, в результате теплопроводности в элементарном объеме останется количество тепла

^d Q T = ^d Q X ^{- d} Q X + d X ^{+ d} Q Y ^-

^{- d} Q Y + d Y ^{+ d} Q Z ^{- d} Q Z + d Z , или

d Q T

I ^d L d T A d

X + d x   d x   d y

V

I x dL)

( a ^y J

d I, dTA) +X dz I   dz J

J

X

d Q X =- X Td d y • dz • d T , d x

x d x d y d z d T ^

Математическая модель описывает тепловое состояние всего блока нагрева/охлаждения

амплификатора, включая источники и стоки тепла. Модель представлена в общем виде, без учета конкретного типа нагревательного элемента и устройства отвода (поглощения) тепла. Мощность внутренних источников теплоты представим как некоторое количество тепла, выделяемого или поглощаемого в элементарном объеме тепловыделяющего или теплопоглощающего элемента конструкции в единицу времени. Обозначив количество тепла, выделяемого в элементарном объеме в единицу времени — Q _V , а удельную мощность внутреннего источника — S , получим:

QV = S • dx • dy • dz • dr .

Поскольку часть теплоты в результате теплопроводности остается в элементарном объеме и, кроме того, присутствуют внутренние источники (стоки) тепла, то энергия данного объема изменяется, т. е. изменяется его температура:

„ d T

Q P = c p — d x d y d z d r . d r

Начальные условия:

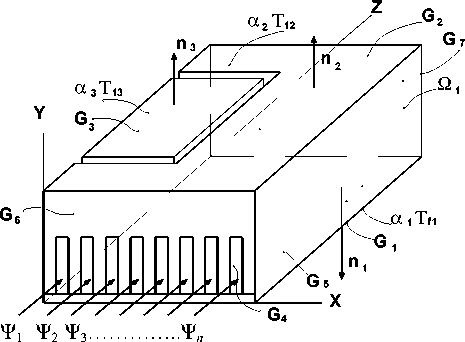
T (Г1-о)= Tо относятся к области (рис. 5)

r ( x , y , z ) e Q 1

и

^{r e} 0, ^r MAX

Граничные условия:

вертикальные поверхности G 5 , G 6 и G 7 , ограничивающие расчетную область Q i — изотермические.

На поверхностях G 1 , G 2 и G 3 , ограничивающих расчетную область Q 1, задаются граничные условия третьего рода. Это означает, что на указанных поверхностях задается зависимость теплового потока за счет теплопроводности со стороны тела от температур поверхности тела Т и окружающей среды (воздуха) T f :

Здесь с — удельная теплоемкость, а р — плотность материала.

Уравнение баланса энергии данного элементарного объема за единицу времени d r имеет вид

Q p = Q v + Q t ,

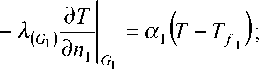
или

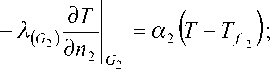
G ₃

d T ср— = dr

d^dtA dLdtAX+X dx( dx J dy dy

d^d T A „ + —I X— 1 + S.dz I dz i

dL

^{Х (} ° з ) э n 3

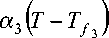
Известно, что коэффициент теплоповодности X зависит от температуры и в некотором ограниченном интерв симировать ли x-x^^T.Y

где Хо — коэффициент теплопроводности при Т0= 273 К, в — экспериментальный коэффициент пропорциональ мости вполне риалов, приме тов рассматрив Математиче вое состояние представляет уравнение

Поток воздуха

Рис. 5. Определение граничных условий. К математической модели теплового состояния

cp^~ = div(- [A]gradГ) + S, dr здесь [Х] — тензор теплопроводности.

Тепловые источники S 1 , S 2 и S 3 , входящие в уравнение теплопроводности, имеют нелинейную по времени характеристику.

Охлаждение радиатора осуществляется потоком воздуха, проходящим через n каналов (рис. 5). Тепловое состояние воздуха в каналах радиатора описывается уравнениями энергии [4, 5]:

Pc^1 + div(p • u • c -01 - [X]grad 01) = 0;

дт

Pc^2 + div(p • u • c • 02 - [X]grad 02) = 0; дт

dPc0n + div(p • u • c • 0n - [X]grad 0n) = 0. дт

Здесь 0 n — текущая температура в j -м канале радиатора (К); u — вектор скорости потока воздуха (м/c); [ λ ] — тензор теплопроводности воздуха (Вт/(м . К)).

Начальные условия для потока воздуха — равенство скоростей потоков на входных участках u 1 (r2 ,0)= u2 (r3 ,0)= - = u 1 (rn+1,0)= u0

и температуры газа в потоках на входных участках

0 1 ( r 2 ,0 ) =0 2 ( г з ,0 ) = ... = 0 1 ( r n + 1 ,0 ) =0 0

— относятся к областям (рис. 5):

r (x,y,z)e ^1, r3(x, y, z )e ^2,

rn+1 (x, У, z)e ^n , где r2, r3, .„ rn, rn+1 — радиус-векторы точек, принадлежащих расчетным областям Ψ1, Ψ2, … Ψn, и

T G [0,TMAX ] .

Условия сопряжения в охлаждающих каналах радиатора задаются согласно закону Фурье на границах стенка канала—воздух

^qG 4

r

I

X 5L

G 4 д n 4

7 ^{- n} 4

= + Xa”^ д n 4 ^

+ n ₄

В данном случае q _{G 4} — плотность теплового потока на границе газ—стенка, а X и X G 4 — коэффициенты теплопроводности воздуха и стенки канала радиатора соответственно.

В поставленном виде расчет теплового состоя-

ния сводится к решению сопряженной задачи. Необходимо совместное решение нестационарного трехмерного нелинейного уравнения теплопроводности для всей рассматриваемой области и уравнений энергии потока воздуха, протекающего в каналах охлаждения.

РЕШЕНИЕ СФОРМУЛИРОВАННОЙ ЗАДАЧИ

Выбор метода решения

При решении задач подобного класса с существенной нелинейностью граничных условий аналитическими методами математической физики встречаются серьезные трудности. Классические методы, к которым относятся метод разделения переменных — метод Фурье, метод функций источников (Грина) и метод тепловых потенциалов, не позволяют решить такие задачи. То же относится и к методам интегральных преобразований: интегральному преобразованию Лапласа, интегральному преобразованию в бесконечных пределах, применению таблиц интегральных преобразований и к конечным интегральным преобразованиям [3]. Известно большое количество методов, позволяющих получать приемлемое решение задач теплопроводности при нелинейных граничных условиях. Прежде всего это метод перехода к эквивалентному интегральному уравнению [3]. Известны методы линеаризующих подставок, которые сводятся к выбору подставок, связывающих искомую температуру с новой функцией таким образом, что краевая задача относительно нее будет иметь линейное граничное условие. Разработаны подставки различных видов [3]. Для исследования процессов в одномерных телах классической формы применяют методы последовательных приближений. Чаще всего этот метод применяют для расчета процесса нагрева термически массивных тел, когда число Био не превышает 0.5 [3]. В теории нелинейного теплопереноса широко используются методы решения нелинейных уравнений в частных производных с малым параметром. Данный метод, часто называемый методом возмущений, заключается во введении небольших поправок к основному решению задачи в виде ряда. Параметрами разложения ряда являются содержащиеся в краевых условиях малые числовые коэффициенты. Метод позволяет решать задачи с нелинейными граничными условиями для тел с практически любыми геометрическими формами [3].

Сегодня к наиболее широко используемым методам решения задач, связанных с исследованием процессов теплообмена, относится математическое моделирование, базирующееся на численных методах решения систем дифференциальных

уравнений в конкретной трехмерной постановке [6]–[9].

Дискретизация задачи

В данной работе для исследования теплового состояния блока нагрева/охлаждения амплифика-тора применен гибридный численный метод решения [4, 10], сочетающий достоинства конечноразностного и конечно-элементного контрольного объема. Предложенный в работе [10] метод дискретизации предполагает разбиение расчетной области на призматические конечные элементы (рис. 6), имеющие в сечении XOY форму треугольника [4]. Обоснование выбора конечного элемента треугольной формы приводится в работе [8]. Данный способ дискретизации предполагает, что при обеспечении заданной точности расчета значительно экономится оперативная память ЭВМ и уменьшается общее время расчета. Последнее важно, несмотря на высокую производительность современных ЭВМ, т. к. при данной дискретизации возможно разбиение расчетной области на 100 000 и более узлов.

Как отмечалось, распределение температуры воздуха в каналах радиатора описывается уравнением энергии

Pc^ + div(p • u • c • © - [A]grad ©) = 0 ,

дт

00 0

[ A ] = 0   X yy

A

zz

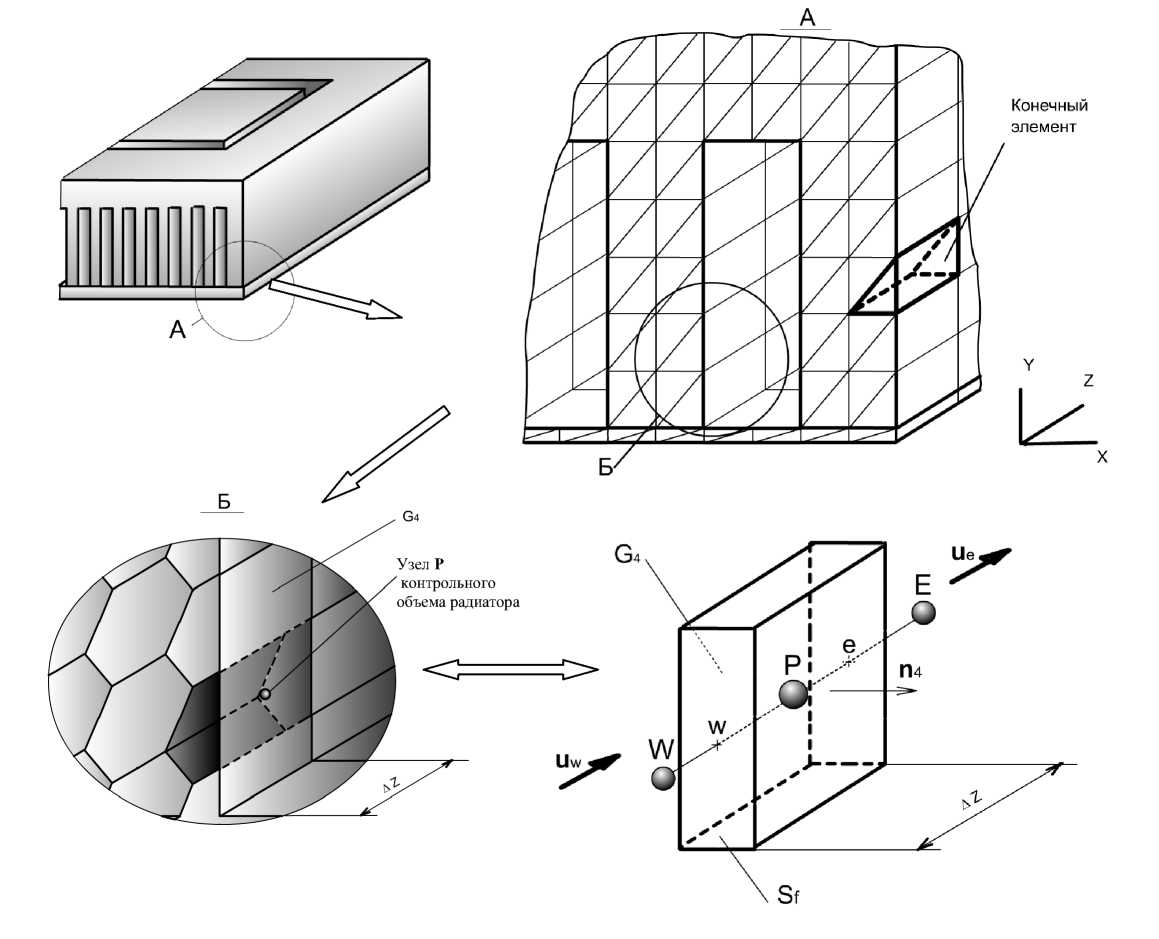
Рис. 6. Построение контрольных объемов и определение граничных условий для сопряженной задачи теплообмена

В соответствии с принятой схемой дискретизации расчетной области для получения дискретного аналога данного уравнения проинтегрируем его по контрольному объему (рис. 6).

Узел P находится в центре контрольного объема. Принимаем допущения:

— значение зависимой переменной в узле P превалирует в контрольном объеме;

— значения теплофизических характеристик потоков зависимых переменных через грани контрольного объема представлены через значения этих величин в центрах соответствующих граней [6].

Интеграл от первого слагаемого, представляющего нестационарную составляющую уравнения, можно представить в виде:

Слагаемое I ₂ представляет собой мощность теплового потока, подведенного к контрольному объему (воздуха) за счет теплообмена со стенками канала охлаждения радиатора:

1 2 = - f ( [ A ] grad 0 , n ) d S = - f X д ПА d S .

Согласно закону Ньютона—Рихмана (в данном случае для конвективного теплообмена между стенками канала и потоком газа) второе слагаемое принимает вид

12 =-[Л—dS = fa(©p - T)dS.

S д n      s p

f

V

др c 0 дт

d V =

^р р c р ⁰ р ^р р с р ⁰ р а v Ат

В данном уравнении T — среднеинтегральная температура боковой поверхности участка A z канала охлаждения в контрольном объеме

^{р р} c ^{р 0 р} А V - ^{Р р} с ^{р 0 р} А V. А т        А т

Здесь А V — величина контрольного объема (м³), А V = S f -A z . Индексами * — обозначены параметры на предыдущем по времени шаге.

Второе слагаемое уравнения энергии потока воздуха принимает вид

f div(puc0 - [X]grad 0)dV =

V

= f ((p u c 0 - Ngrad 0), n)dS =

S

= f p c 0 ( u , n ) d S - f ( [. Л ] grad 0 , n ) d S = 1 1 + 1 2 .

SS

Проведем дальнейшее интегрирование на основе предложенного в работе [6] метода (см. рис. 6):

11 = f pc 0(u, n)dS =

S

= f pc 0(u, n)dS + f pc 0(u, n)dS =

S e                    S w

= ce 0 eG + cw 0 wG.

T = -1- f TdS ;

S б _{S б}

S ₆ — площадь боковой поверхности канала в рассматриваемом контрольном объеме; а а — коэффициент теплоотдачи от газа к стенке канала, (Вт/(м² - К)).

Таким образом,

1 2 = а 0 _p S _б - a TS _б.

Для получения дискретного аналога проведем дальнейшее преобразование уравнения энергии с учетом полученных зависимостей:

^p p c p ^А V ⁰ p

Ат

V

+ c e G 0 e

+ a S б 0 p

AV ^

А V /

* * ™*

p PcP А V 0 P

—

Ат

V

-

c w G 0 w + a S б T А Т . ^А V j

Согласно противопоточной схеме, предложенной в [6], примем, что (см. рис. 6)

u e u P , u w = u W .

Тогда

Здесь G = f pu dSf — расход воздуха в канале ох-Sf лаждения радиатора, протекающего через соответствующую грань Sf контрольного объема (рис. 6).

Слагаемое 1 1 представляет мощность потока энергии, подведенного к контрольному объему расходом газа, обладающего внутренней энергией.

f p p c p ^А V

Ат

V

* *

= ppcp0

Ат

+ cpG +    А V ^0

^p А V

*

p

- А V - cwG0 w

p

+ aSA а v , А V

^р p c p ^А V

А т

V

**

_ р p c p ⁰

Ат

*

р

- А V + C w G 0 w

+ cG +   А V ^0

^e    А V

p

+оа а v , А V или в общепринятой форме дискретный аналог уравнения теплопроводности принимает вид ap0p = aw0w + b •

Здесь aw = CwG ,

= ^{P p}c^{p А} V + c e G + S _P А V ,

**

b = ppCpАV 0*+ s av , Ат где SP

^{a S} б

А V

и S _C

a S _б T А V

Решение сопряженной задачи в дискретной форме

Как уже указывалось, для решения данной задачи в поставленном виде необходимо одновременное решение системы уравнений, включающих уравнения нестационарной теплопроводности в трехмерной постановке, описывающие тепловое состояние всего устройства, и уравнение энергии для потока газа, протекающего во всех каналах охлаждения радиатора. Взаимодействие происходит в зоне контакта потока воздуха со стенками каналов охлаждения радиатора. Для решения дискретного аналога уравнения теплопроводности необходимо определить распределение температуры потока воздуха в каждом канале. Кроме того, необходимо знать коэффициенты теплоотдачи, для расчета которых существует ряд методик, но в любом случае необходимо знать распределение температуры по стенкам канала охлаждения. Решение данной задачи базируется на сопряжении тепловых потоков на границе разделения поверхности канала, контактирующего с потоком воздуха и объемом воздуха в канале. В данном случае для решения дискретного аналога уравнения энергии потока воздуха строится контрольный объем, ограниченный стенками канала охлаждения и двумя поперечными сечениями в пределах канала на расстоянии d z друг от друга.

Тепловой поток от стенки к j -му контрольному объему потока воздуха:

Q j = J a j ( 0 j - T j ) d S = J a j 0 j d S - J a j T j d S . S   SS

Соответственно первое слагаемое можно представить как

J aj0jdS = 0ja^j.

S

Здесь S _j — боковая поверхность j -го контрольного объема. Общая боковая площадь канала охлаждения, контактирующего с потоком воздуха, m

S _б j = ^ S kj , где m — общее число контрольных k = 1

объемов в канале.

Аналогично можно представить и второе слагаемое уравнения — тепловой поток от стенки к j -му контрольному объему потока воздуха

J a j T _{5 y} d S = a j TS -, •

S

Следовательно,

Q _J = 0 _J a _J S -j - T a S - •

Тепловой поток для контрольных объемов радиатора, образующих канал, определяет граничные условия, т. е. представляет источник тепла для уравнения теплопроводности

e.j= ajtijk -ej.

Таким образом, исходя из принципа сопряжения тепловых потоков

m

S Q kj + Q j = 0.

k = 1

Граничные условия на поверхностях сопряжения потока воздуха со стенками канала можно записать как aJ(тJ-eJ')=

λ

V

d T .)

d n

/

G ₄

где черта над переменной означает ее усреднение.

Для расчета среднего значения коэффициента теплоотдачи a j по поверхности теплообмена воспользуемся зависимостью [13]

Я , a_; = Nu_; —. _d

Здесь d есть некоторый эквивалентный диаметр для расчета канала сложной формы, который мож-4Sf но рассчитать как dj = ——, где Sf — площадь сечения канала, а L — периметр сечения канала.

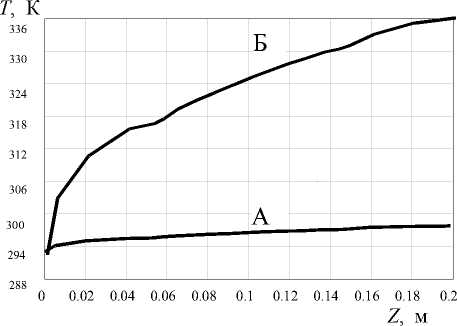
Рис. 7. Распределение температуры воздуха по длине Z канала охлаждения: А — в процессе циклического нагрева пластины-держателя, Б — в процессе охлаждения пластины-держателя

Проблема заключается в том, что отсутствуют достоверные критериальные зависимости для вычисления коэффициента Нуссельта для каналов сложной формы с граничными условиями второго рода. В данной работе используется подход, предложенный в [12] и опробованный в работах [4, 11]. Авторы работы [12] провели исследования теплоотдачи в трубах при сложном сопряженном теплообмене, используя при этом предложенные в [13] критериальные зависимости для плотности теплового потока q = const:

Nu

Nu ~

= 1 +

+ 0.416 Pr - °' ⁴ I ^— I ⁴ X

I d J

T , К

285 0

а

Пластина-держатель

Радиатор

800 t , c

X 1 +

I

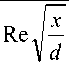
f exp

I

0.17^f - ( d

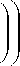
Данное соотношение справедливо для диапазона критерия Рейнольдса 4 - 10 3 <  Re <  10⁶, критерия Прандтля 0.7 <  Pr <  100 и отношений длины трубы к диаметру ( х / d ) >  0.5.

Значение Nu _го при постоянной плотности теплового потока q = const в работе [13] предложено рассчитывать как

Nu

^

| — I Re Pr ( 8 J

k + 12.7 I ^— Pr³ - 1

v J

T , К    б

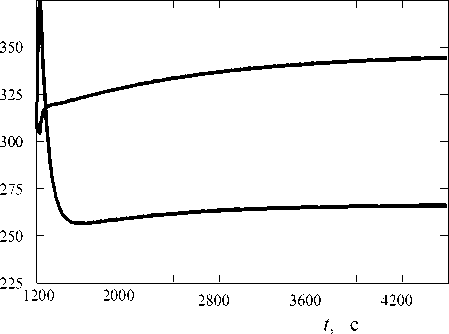
Рис. 8. Расчетные значения усредненных температур пластины-держателя и радиатора в процессе циклического нагрева (а) и охлаждения (б)

Здесь — — коэффициент местного сопротивления трубопровода

— = ( 1.82lgRe - 1.64 )^{- 2},

k = 1 + 900/Re.

Выражение для расчета Nu ^ справедливо при 10 4 <  Re <  5^10 6 и 0.5 <  Pr <  200.

ЗАКЛЮЧЕНИЕ

Для решения поставленной задачи, а именно расчета теплового состояния блока нагре-ва/охлаждения амплификатора на основе созданной математической модели, была разработана программа расчета на языке программирования FORTRAN с использованием программного

а

T: 299.6 306.2 312.9 319.5 326.1 332.7 339.3 345.9 352.6 359.2

0.025

б

0.05

0.1

X

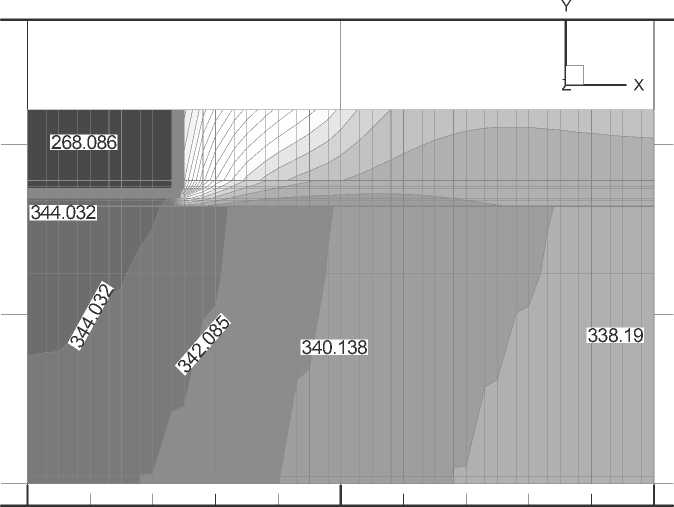
Рис. 9. Температурное поле блока нагрева/охлаждения амплификатора в режиме циклического нагрева (а); б — поперечный разрез блока при расчете режима охлаждения комплекса FEM-CV, созданного на кафедре "Теплофизика" Московского государственного технического университета им. Н.Э. Баумана [4]. Программный комплекс предназначен для решения трехмерных нестационарных нелинейных задач тепло- и массопереноса. Сопоставление полученных результатов расчета с результатами экспериментальных исследований показали приемлемую сходимость. Созданная математическая модель расчета теплового состояния блока нагре-ва/охлаждения использовалась в процессе разработки амплификаторов "Циклотемп-105" и "Циклотемп-107". В процессе разработки конструкции амплификаторов были проведены серии расчетов, позволивших получить оптимальное соотношение геометрических размеров основных элементов конструкции. На рис. 7 приведены результаты расчета распределения температуры воздуха по длине канала охлаждения: А — в процессе циклического нагрева пластины-держателя, Б — в процессе перевода пластины-держателя в режим длительного охлаждения до температуры 277 К. На рис. 8 приведены расчетные значения усредненных температур пластины-держателя и радиатора охлаждения при работе амплификатора в циклическом режиме (а) и в режиме охлаждения (б). На рис. 9 приведен результат расчета температурного поля блока нагрева/охлаждения в режиме циклирования в момент времени 1202 с (а) и поперечный разрез блока при расчете режима охлаждения (б).