Основы теории силового импульсного устройства
Автор: Ниязов Нурпазыл Тажибаевич, Джаманкызов Насипбек Курманалиевич, Асанов Арстанбек Авлезович, Исманов Юсупжан Хакимжанович
Журнал: Бюллетень науки и практики @bulletennauki
Рубрика: Технические науки
Статья в выпуске: 6 т.7, 2021 года.
Бесплатный доступ
В статье рассмотрена математическая модель силового импульсного устройства, которая позволяет подбирать характеристики выбрасываемой струи жидкости, такие как скорость в момент выброса, давление, создаваемое в сопле силового импульсного устройства и др., изменяя параметры устройства. Особенностью предложенной математической модели, существенно отличающей ее от ранее рассмотренных моделей, является то, что модель рассматривалась для случая неустановившегося движения. Такое состояние среды в силовом импульсном устройстве является наиболее характерным, поэтому полученные результаты являются более общими. Показано, что в отличие от установившегося движения жидкости, в случае неустановившегося движения появляется дополнительное слагаемое, которое можно определить как напор, носящий инерционный характер. Из предложенной математической модели видно, что наличие инерционного напора приводит к возникновению эффекта торможения потока, что, в свою очередь, приводит к возрастанию полного напора жидкости в направлении течения потока. Напор, возникающий в стволе, действует против направления гидравлических сопротивлений. Все сказанное применимо лишь для определенного момента времени или для случая, когда ускорение жидкости постоянно. Если же ускорение меняется, то действие напоров вдоль течения жидкости является функцией времени. Это обстоятельство дает возможность применять полученный результат при неустановившемся движении для создания устройств, формирующих струю высокого напора. Отличительной особенностью рассмотренной модели является то, что здесь анализируется поведение жидкости в силовом импульсном устройстве для двух случаев: 1) объем жидкости в стволе силовой импульсной установки больше, чем объем сопла; 2) объем жидкости в стволе меньше или равен объему сопла. Результаты анализа показали, что в первом случае начальная скорость выброса жидкости значительно превышают эту скорость во втором случае. Т. е. именно первый случай имеет практическое значение.
Силовое импульсное устройство, сопло, инерционный напор, неустановившееся движение, скорость, давление
Короткий адрес: https://sciup.org/14120573
IDR: 14120573 | УДК: 532.522: | DOI: 10.33619/2414-2948/67/16
Текст научной статьи Основы теории силового импульсного устройства
Бюллетень науки и практики / Bulletin of Science and Practice
УДК 532.522: 518.5
В настоящее время произошел бурный рост в использовании водоструйных технологий, основанных на применении струй жидкости высокого и сверхвысокого давления, в различных отраслях промышленности. Данные технологии используются для обработки бетонных поверхностей (резка, очистка, углубление), разрушения горных пород и бетонных блоков, упрочнения металлических поверхностей наклепом при ударе струи, очистки корпусов судов от ракушек и старой краски и т. д. Характерной особенностью водоструйных технологий является возможность обработки материалов, существенно различающихся по своим механическим свойствам — пластмассы, кожи, мягких, твердых и хрупких металлов, горных пород и бетонных изделий различной прочности и абразивности. Обрабатывающим инструментом в этих процессах является, как правило, вода, которая в отличие от других инструментов не тупится и не требует заточки. В этом смысле рассматриваемые технологии являются универсальными, т. к. не требуют замены рабочего органа при смене обрабатываемого материала [1].
Производительность водоструйных технологий быстро возрастает при увеличении давления воды, поэтому целесообразно использование струй жидкости высокого и сверхвысокого давления. Однако получение стационарных струй с такими параметрами в настоящее время сталкивается с большими техническими трудностями. По этой причине все большее распространение получают пульсирующие и импульсные струи жидкости высокого и сверхвысокого давления, эффективность которых значительно превышает стационарные струи. Формирование струй воды супервысокого давления требует оборудования, создающего высокий напор и использующего неустановившиеся процессы в рабочей жидкости. Например, в гидравлических вибрационных прессах, гидравлических молотах, гидроперфораторах, гидропушках и импульсных водометах создание значительных импульсов является необходимым для обеспечения их основных функций [1–2].
Основные гидродинамические параметры ультраструй — максимальная скорость струи, ее компактность, дальнобойность и коэффициент превышения давления существенно зависят от механизма ускорения жидкости в этих установках. Зависимость этих параметров от формы сопла и других конструктивных факторов гидропушки достаточно подробно исследована в [3–5]. Однако в литературе отмечается, что закономерности получения таких струй и их воздействия на объект обработки еще недостаточно изучены [6–8].
В частности, применение неустановившегося движения в рабочей жидкости для описания процесса формирования высоконапорных струй в литературе практически отсутствуют, за исключением [1]. Поэтому целью настоящей работы является теоретическое исследование процесса преобразования энергии в силовом импульсном устройстве (СИУ) для получения струйных импульсов жидкости, обладающих супервысокой скоростью, этим методом.
Математическая модель СИУ
Рассмотрим задачу аналогичную той, которая рассмотрена в работе [1]. Покажем, что применяемый нами метод на основе неустановившегося движения дает тот же результат, что получен в работе [1]. Схематичное изображение поршневой СИУ приведено на Рисунке 1.

Рисунок 1. СИУ. 1 – ресивер; 2 – поршень; 3 – столб воды; 4 – ствол установки; 5 – сопло
Из рисунка видно, что пар под высоким давлением 1 заставляет двигаться поршень 2 и столб воды перед ним 3 вдоль ствола 4 до определенной скорости. С этой скоростью вода втекает в сужение сопла. Это происходит в тот момент, когда передний фронт водяного столба оказывается у входа в сопло 5. Жидкость в районе переднего фронта получает ускорение. Остальная часть жидкости и поршень, наоборот, притормаживаются. Это означает, что в установке начинается неустановившейся процесс. Поршень и прилежащая к нему жидкость сообщают энергию частицам жидкости, расположенным спереди, что приводит к значительному увеличению их скорости. Смещение жидкости в СИУ можно рассматривать как одномерное, что не сильно влияет на общность рассуждений. Также считаем, что вязкость и сжимаемость жидкости, деформация корпуса пренебрежимо малы.
Для переднего фронта потока жидкости делаем предположение, что он плоский. И, наконец, последнее допущение — не учитываем давление воздуха в сопле.
За начало координат берем начало сопла. Передний фронт жидкости в начальный момент времени располагается именно здесь. По определению неустановившееся движение потока жидкости характеризуется временной зависимостью его параметров — скорости, давления и плотности во всех точках жидкости. В принятой постановке уравнение Бернулли для неустановившегося движения идеальной несжимаемой жидкости в СИУ для двух сечений, проходящих через задний фронт водяного заряда и произвольную точку внутри сопла, можно записать в виде [9–10]:
f « + “ 1 = JL +(1+<) 2 2 + Lft^ (1)
pg 2g i> g 2'2g gJxRdt
Начальные и граничные условия имеют вид:
u(0,x)=u0, p(0,x)=0, -L< x > 0,xR(0) = -L, (2)
xF (0)=0, u(t, xR )= uR, p(t, xF)=0 , где u, p, p — такие важные характеристики элемента жидкости, как скорость, давление, плотность; д — ускорение силы тяжести; x — координата; t - время; и0 — скорость поршня в начальный момент времени; xR и xF — координаты, определяющие положения фронтов водяного заряда — заднего и переднего соответственно; uR — скорость заднего фронта; L — длина столба воды; Ls — длина сопла. R и F — индексы, характеризующие параметры заднего и переднего фронтов соответственно, ^ — суммарный коэффициент гидравлических сопротивлений, который для данной системы — величина постоянная. Максимальное значение координаты переднего фронта xF = Ls.
При установившемся движении, если между двумя сечениями нет источника энергии (насос и др.), то, благодаря трению, удельная энергия во втором сечении вдоль направлении течения потока жидкости всегда меньше, чем в первом сечении. В отличие от установившегося движения жидкости в случае неустановившегося движения справа
1 X du появляется дополнительное слагаемое hi = - J^ — ax, которое можно определить как напор, носящий инерционный характер. Физическая суть напора, носящего инерционный характер, как видно из соотношения (1), это результат вычитания полных напоров, которые можно рассматривать как суммарные значения энергии жидкости, отнесенные к единице веса жидкости, в произвольных сечениях S1 и S2 , в данный момент времени. Эта разность обусловлена отрицательным или положительным значениями ускорения потока жидкости. Положительное ускорение приводит к положительной разности напоров в указанных сечениях. Т. е. полный напор уменьшается в направлении движения потока, что сходно с действием гидравлических сопротивлений на напор. Если ускорение направлено против движения потока, то напор на сечение S1 становится больше, чем на сечение S2 . Т. е. эффект торможения потока приводит к возрастанию полного напора жидкости в направлении течения потока. Напор, возникающий в стволе, действует против направления гидравлических сопротивлений. Все сказанное применимо лишь для определенного момента времени или для случая, когда ускорение жидкости постоянно. Если же ускорение меняется, то действие напоров вдоль течения жидкости является функцией времени. Это обстоятельство дает возможность применять инерционный напор при неустановившемся движении для создания установок, формирующих струю высокого напора.
В уравнения неустановившегося движения (1) фигурируют две неизвестные функции — скорость и давление. Ясно, что для определения этих функций необходимо иметь еще одно уравнение. Этим уравнением является уравнение неразрывности, которое, учитывая принятые ограничения (пренебрежение сжимаемостью жидкости и деформируемостью корпуса), имеет вид:
д-^1 = 0. (3) дх
Это означает, что величина uF, представляющая собой расход жидкости, является функцией только времени, т. е. uF= f(t). Отсюда следует, что для любого фиксированного момента времени расход жидкости во всех сечениях потока одинаковый [2]:
U r F r = u(t, x)F(x) = usFs . (4)
s — индекс, характеризующий параметры на выходной кромке сопла. F= F(x) — функция координат, являющаяся площадью поперечного сечения сопла.
Процесс выброса жидкости СИУ можно разделить на два этапа: первый этап, это когда жидкость попадает в сужение сопла, второй этап представляет собой непосредственно выброс порции жидкости из сопла.
Этап втекания жидкости — это начало процесса выброса жидкости СИУ. Данный этап завершается в тот момент, когда передний фронт столба жидкости оказывается у выходной кромки сопла. Как указано выше, процесс втекания водяного заряда в сужающееся сопло сопровождается торможением потока вместе с поршнем. В уравнении, описывающем движение жидкости обязательно надо учесть движение поршня:
mpUp = - pRFR, X p = up, up (0) = u o , X p (0) = -L. (5)
Здесь u p = uR , — скорость, сообщенная поршню; X p =x0- координата положения поршня; pR - давление, оказываемое на поршень. Временную производную обозначаем точкой над соответствующей переменной. Выразим из уравнения (1) скорость u через скорость заднего фронта uR / u = u R F R / F(x). Учитывая (5) получим распределение давления вдоль водяного столба:
Р<‘> x) = - ^(W -1) (1+0 - u'rG? + PFR ^ ).
Однако надо учитывать, что инерционный напор имеет различный вид в зависимости от того, больше или меньше объем воды в стволе, чем объем воды в сопле на начало истечения. Указанное соотношение объемов зависит от длины сопла.
Случай а). Если объем жидкости больше объема сопла, то на начало истечения поршень находится в стволе и выражение для инерционного напора имеет вид:
„гх dx о \r0 dx , г-x dx \ „Г xR , rx dx 1
J0 F(x) I'
PFR Ix,^ = PFR [L^ + foF^> J = P F R I - FT +
В этом случае распределение давления по длине водяного заряда принимает вид:
p(t, x) = - ^iS -1) 0+0 - u R (^- X R P + PFR Jo^ )
Ускорение заднего фронта жидкости U r найдем из выражения (7) с учетом граничного условия на свободной поверхности p(t, xF ) = 0:
- X P FrU^, Fr , fX dx 1 1
uR (t, x) = - —rA^ -1) (1 + ^ [ mP - xR P FR + P FR ^ 0 F(X) ]
Приведенные формулы полностью описывают втекание жидкости в сопло СИУ и дают распределение скоростей и давлений по длине водяного заряда в разные моменты времени или положения переднего фронта в зависимости от величины водяного заряда. Поршень и прилежащая к нему жидкость сообщают энергию частицам жидкости, расположенным спереди, что приводит к значительному увеличению их скорости.
Выход струи из сопла приводит к уменьшению массы и энергии жидкости в СИУ.
Обозначим момент выхода струи из сопла t0. Рассмотрим произвольный момент времени, удовлетворяющий условию t > t0. К этому моменту сопло покидают жидкость массой Am и энергия AE. Принимая во внимание соотношение Ur(t,x) = uR ^и~^-, получаем из уравнения (8):
du R _ dx R
ju^ji-«d+f ) m»- x"pFR + ^R'f'fS) '
2 F(x)
Далее, делая замены переменных:
k 1 = m „ + P FR !’r- dy и k2 2^ -1 ) (1+«.
Принимая во внимание начальные условия на момент выброса жидкости из ствола, получаем, после интегрирования соотношения (9), выражение для скорости заднего фронта жидкости как функцию координаты:
Ur =URq
/ k1-pFR XR k 1-pFR xR 0
)
^ 2
Здесь xRo и uRq — координата и скорость заднего фронта на начало выброса жидкости из ствола, которые рассчитываются на основе законов сохранение массы и энергии в момент завершения втекания. Когда передний фронт водяного заряда доходит до среза сопла, его задний фронт сдвинется на расстояние xR , значение которого можно определить из закона сохранение массы m = PFr Xr0 + pJ^FF^dx.
Отсюда:
Xr = — - — LXFF(x)dx.
Ro pFr Fr J0
Скорость в этой точке получим из закона сохранение энергии:
uR0 = —
J mp
(m+mp)u0 ______
2 rxF dx
- pFr XRo+ pFr/oF(X)
Знание этих выражений позволяет находить значение момента времени t0, при котором начинается истечение:
= XRo t0
u^o
Бюллетень науки и практики / Bulletin of Science and Practice Т. 7. №6. 2021
Соотношение, представляющее собой временную зависимость положения заднего фронта xR на этапе испускания жидкости из сопла, получаем, проинтегрировав уравнение dxR
(11), и так как uR = -^- t =
t + (т+тр)и0
0 (k2 - 1)Р F R U3R 0
I (
^1—PFRxR k1-pFR xR0
Г-I .
Здесь учтено, что к 1 — pFR xRo = (т + тр)и 2 /и 2 .
Из выражений (15) и (11) получаем соотношения, показывающие зависимости координаты и скорости заднего фронта от времени:
kj
X r = PF R
k1-p F R xR 0
(^2— 1>P FR иУ pFR 1 +--—-- 2 ° ( t- f0 )
(m+mp)u0
k2-1’
U r = UR 0
L (k2 - 1)p F R UR 0 (т+тр)и2
( t —
^ 0)]
^2
^2-1
Для скорости выброса жидкости из ствола получаем:
us = U r — = U r0
r 1 + < k£22^R u S„( t
L (т+тр)и 0
—
^ 0)]
^2 k2-1F R
F s
Как видно из этих соотношений, скорость выброса жидкости из ствола в kF = — раз Fs 2
превышает поршневую скорость. В начальный момент выброса жидкости из ствола СИУ скорость выброса максимальна и равна:
и5мах kFuR0 -
Важной особенностью выброса является то, что скорость выброса сильно ослабевает со временем.
Случай б). Если объем жидкости в стволе меньше или равен объему сопла, то на начало истечения поршень остановится у входа в сопло, а вся жидкость окажется внутри сопла. В х dx этом случае инерционный напор pFr ^. можно записать в виде
„ с х dx Р R Ч) F(x) .
Здесь учитывается, что координата заднего фронта водяного заряда xr =0. Уравнения (7) и (8) в этом случае принимают вид:
P", x) = - ^ FF R22 -1) (1+0 - ^^
и, с учетом граничного условия на свободной поверхности p(t, xf ) = 0,
U r (t, x) = - ^
После интегрирования (21) по времени получаем зависимость скорости заднего фронта от времени: Бюллетень науки и практики / Bulletin of Science and Practice
U
r
=
uRo l+^^p Fr (t-to),
где
k=mp
+
pF
R
^F
F^
. (23)
, _ „ (m+mp^uO ~
Здесь
ur
= -------
x dx
, и его можно определить из закона сохранения энергии. Это
0
mrn++ p
F£S
o
F
FX)
значение скорости заднего фронта водяного заряда в цилиндрическом стволе в момент времени, когда жидкость начинает втекать в сопло. В конце втекания вся жидкость находится в сопле, но истечения жидкости еще нет. Исходя из сказанного, получаем для времени разгона водяного заряда в сопле следующее соотношение t0=
L/
u
Ro
.
Соотношение для зависимости скорости истечения жидкости от времени в рассматриваемом случае имеет вид: Fr_ uRo
■ p
F
r
(t-to)^
Us
UR
л
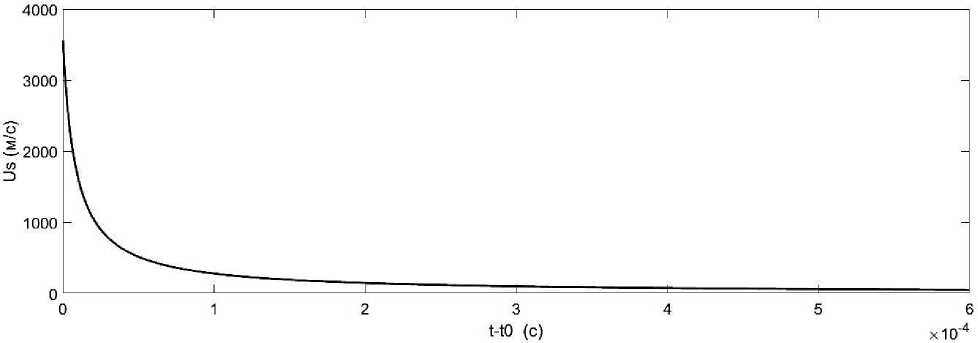
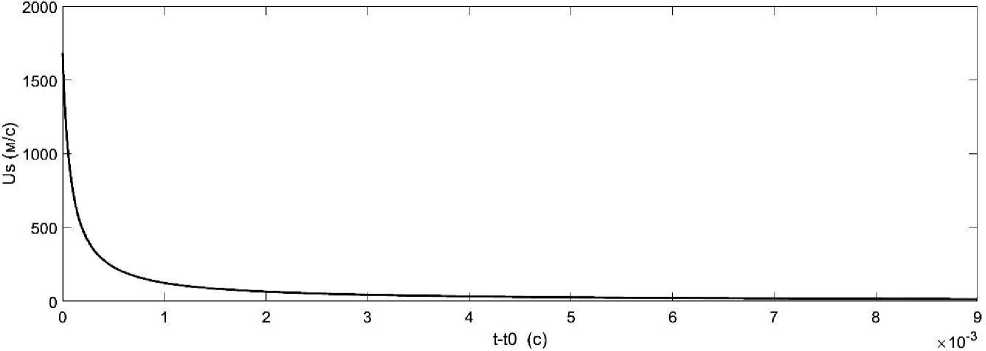
Fs 1+ uRokO ' к Рисунок 2. Зависимость скорости жидкости от координаты в стволе СИУ на момент начала выброса жидкости. 1-раствор без глины; 2-раствор с глиной; 3-вода На Рисунке 2 представлены графики зависимости скорости жидкости от координаты вдоль столба жидкости в стволе СИУ. Графики построены для момента времени, когда начинается испускание жидкости через сопло. На Рисунках 3 и 4 представлены зависимости скоростей истечения жидкости из сопла СИУ для двух случаев: 1. объем жидкости в стволе превышает объем сопла; 2. объем жидкости в стволе меньше или равен объему сопла. Как видно из рисунков в первом случае начальная скорость выброса жидкости превышает начальную скорость во втором случае больше, чем в два раза, а время выброса меньше в первом случае, чем во втором приблизительно в 15 раз. Полученные результаты объясняются тем, что во втором случае, после достижения среза сопла передним фронтом жидкости, вся жидкость оказывается в сопле, и воздействие такого силового фактора, как поршень, отсутствует. В первом случае, даже при полном заполнении сопла жидкостью, часть жидкости остается в стволе, что приводит к продолжающемуся воздействию поршня на жидкость. Рисунок 3. Зависимость скорости истечения жидкости из сопла для случая, когда объем жидкости превышает объем сопла Рисунок 4. Зависимость скорости истечения жидкости из сопла для случая, когда объем жидкости меньше или равен объему сопла Выводы Разработана математическая модель силовой импульсной установки, которая позволяет подбирать характеристики выбрасываемой струи жидкости, такие как скорость в момент выброса, давление, создаваемое в сопле силовой импульсной установки и др., изменяя параметры установки. Особенностью предложенной математической модели, существенно отличающей ее от ранее рассмотренных моделей, является то, что модель рассматривалась для случая неустановившегося движения. Такое состояние среды в силовой импульсной установке является наиболее характерным, поэтому полученные результаты являются более общими. Показано, что в отличие от установившегося движения жидкости в случае неустановившегося движения появляется дополнительное слагаемое, которое можно определить как напор, носящий инерционный характер. Физическая суть напора, носящего инерционный характер, это результат вычитания полных напоров, которые можно рассматривать как суммарные значения энергии жидкости, отнесенные к единице веса жидкости, в произвольных сечениях S1 и S2 , в данный момент времени. Эта разность обусловлена отрицательным или положительным значениями ускорения потока жидкости. Положительное ускорение приводит к положительной разности напоров в указанных сечениях. Т. е. полный напор уменьшается в направлении движения потока, что сходно с действием гидравлических сопротивлений на напор. Если ускорение направлено против движения потока, то напор на сечение S1 становится больше, чем на сечение S2 . Т. е. эффект торможения потока приводит к возрастанию полного напора жидкости в направлении течения потока. Напор, возникающий в стволе, действует против направления гидравлических сопротивлений. Все сказанное применимо лишь для определенного момента времени или для случая, когда ускорение жидкости постоянно. Если же ускорение меняется, то действие напоров вдоль течения жидкости является функцией времени. Это обстоятельство дает возможность применять полученный результат при неустановившемся движении для создания установок, формирующих струю высокого напора. Важным моментом предложенной модели является то, что в ней были рассмотрены два случая: 1. объем жидкости в стволе превышает объем сопла; 2. объем жидкости в стволе меньше или равен объему сопла. Анализ показал, что в первом случае начальная скорость выброса жидкости значительно превышает начальную скорость во втором случае и, поэтому этот случай имеет практическое значение.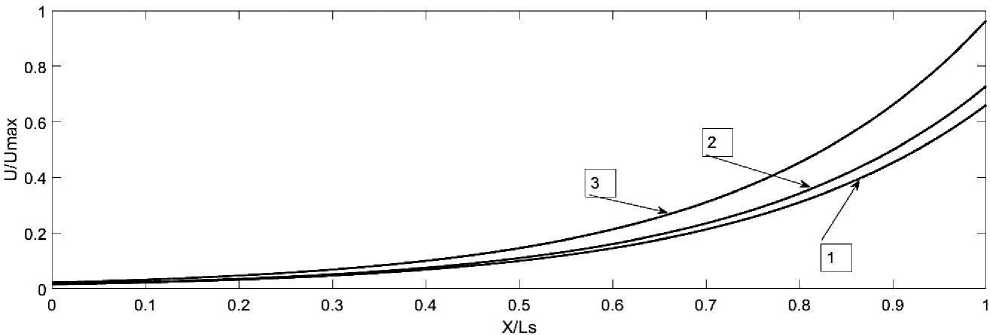
Список литературы Основы теории силового импульсного устройства
- Атанов Г. А. Гидроимпульсные установки для разрушения горных пород. Киев: Вища школа, 1987. 155 с.
- Семко А. Н. Импульсные струи жидкости высокой скорости и их применение. Донецк, 2014. 149 с.
- Gmelin C., Zander V., Hecklau M., Thiele F., Nitsche W., Huppertz A., Swoboda M. Active flow control concepts on a highly loaded subsonic compressor cascade: résumé of experimental and numerical results // Journal of turbomachinery. 2012. V. 134. №6. DOI: 10.1115/1.4006308
- Kirtley K. R., Graziosi P., Wood P., Beacher B., Shin H. W. Design and test of an ultralow solidity flow-controlled compressor stator. 2005. DOI: 10.1115/1.1860374
- Овсепян В. М. Гидравлический таран и таранные установки. М.: Машиностроение, 1968. 173 с.
- Новиков С. Г., Глаголев Р. В., Зайцев С. А. Некоторые аспекты применения гидродинамического эффекта получения сверхвысоких давлений и больших скоростей струи жидкости // Актуальные проблемы общества, науки и образования: современное состояние и перспективы развития: материалы III международной научно-практической конференции. М.: Перо, 2016. С. 283-287
- Hecklau M., Wiederhold O., Zander V., King R., Nitsche W., Huppertz A., Swoboda M.Active separation control with pulsed jets in a critically loaded compressor cascade // AIAA journal. 2011. V. 49. №8. P. 1729-1739. DOI: 10.2514/1.J050931
- De Luca L., Girfoglio M., Chiatto M., Coppola G. Scaling properties of resonant cavities driven by piezo-electric actuators // Sensors and Actuators A: Physical. 2016. V. 247. P. 465-474. DOI: 10.1016/j.sna.2016.06.016
- Dzhamankyzov N. K., Ismanov Y. K., Zhumaliev K. M., Alymkulov S. A. Estimation of optimal hologram recording modes on photothermal materials // Optical Engineering. 2018. V. 57. №1. P. 017113. DOI: 10.1117/1.OE.57.1.017113
- Dzhamankyzov N. K., Ismanov Y. K. Temperature modes of development of holograms recorded on photothermoplastic media heated by laser radiation // Optical Engineering. 2018. V. 57. №6. P. 067103. DOI: 10.1117/1.OE.57.6.067103


