Особенности анализа динамических нагрузок привода вращения механизмов космического аппарата

Основными особенностями разрабатываемого типоразмерного ряда универсальных мехатронных модулей (УММ) является модульная конструкция, малые масса и габаритные размеры, высокая удельная мощность и универсальность применения. Модульная конструкция позволяет быстро модифицировать УММ в соответствии с конструктивными особенностями и техническими требованиями отдельных узлов и механизмов космического аппарата (КА). Модули предназначены для применения в системах ориентации антенн, устройствах позиционирования солнечных батарей, манипуляторов.

Анализ влияния динамических нагрузок на объект разработки на этапе проектирования позволяет доработать и улучшить разработанную конструкцию до начала проведения испытаний. Динамические нагрузки характеризу-

ются быстрым изменением во времени и возникают под действием вибрационной нагрузки. Возникновение динамических нагрузок при эксплуатации УММ связано с воздействием ускорений и сил инерции, возникающих в процессе вывода космического аппарата на орбиту.

Динамический анализ необходим для проектирования структурных и механических систем, работающих без потери устойчивости и последующего разрушения в динамических средах, а также подбора характеристик разрабатываемой системы (формы, механизмов демпфирования, свойств материала, и т.п.), чтобы уменьшить влияние вибрации [1, 2].

В качестве современного подхода для выполнения динамического анализа применяется метод конечных элементов (МКЭ). По результатам МКЭ можно выявить узлы конструкции, требующие доработки для повышения стойкости к механическим воздействиям. МКЭ позволяет оптимизировать процесс разработки, снизить затраты на изготовление макетных и экспериментальных образцов, ускорить проведение испытаний. Такой подход широко применяется из-за высокой степени точности совпадения результатов расчетов и испытаний [3-9].

Цель настоящего исследования заключается в создании конечно-элементной модели (КЭМ) исполнительного прецизионного мехатронного модуля (УММ-ИП) и проведении динамического анализа нагрузок и переходных процессов, возникающих при работе УММ-ИП.

1.    Созданиеконечно-элементной модели

Исследуемый УММ-ИП конструктивно состоит из гибридного шагового двигателя, планетарной и волновой передачи, датчика углового положения типа «вращающийся трансформатор». Кинематическая схема представлена на рис. 1.

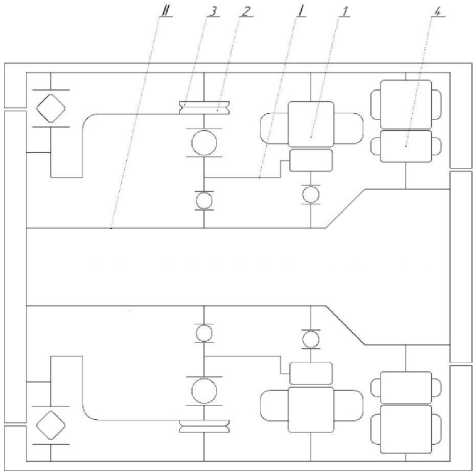
Рис. 1. Кинематическая схема устройства:

I – входной вал; II – выходной вал;

1 – гибридный шаговый двигатель;

2 – гибкое колесо волнового редуктора;

3 – жесткое колесо волнового редуктора;

4 – вращающийся трансформатор

Для проведения анализа динамических нагрузок используется конечно-элементная модель (КЭМ), которая была разработана с помощью Ansys Workbench аналогично имитационной модели, представленной в статье [10]. Для уменьшения времени расчета и накапливаемой ошибки трехмерная модель УММ-ИП упрощена за счет удаления фасок и скруглений, не участвующих в расчете.

Отличительной особенностью КЭМ для проведения динамического анализа является то, что вместо подвижного соединения «Revolute Joint», при котором соединение между поверхностями считается абсолютно жестким, что недопустимо для проведения динамического анализа, используется функция «Bearing», которая позволяет представить подшипник как систему пружин с заданной жесткостью и создает конечный элемент типа «COMBI214», представленный на рис. 2.

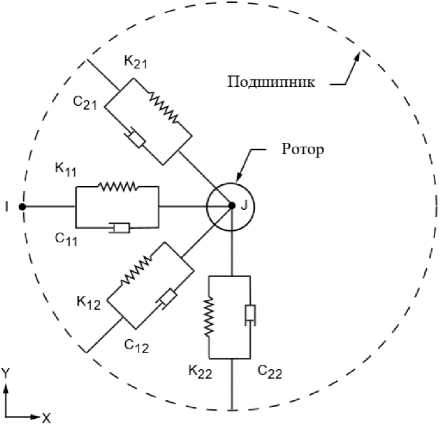
Рис. 2. Изображение элемента COMBI214

Данный элемент позволяет задать коэффициенты матрицы жесткости подшипника – K ₁₁, K ₁₂, K ₂₁, K ₂₂. Матрица жесткости:

	Г к 11	K 12	- K 11	- K 12
[ K e ] =	K 21 - к 11	K 22 - K 12	- K 21 K 11	- K 22 K 12
	1— K 21	- K 22	K 21	K 22 V
Элемент «COMBI214»			не исключает		переме-

щения тел вдоль оси вращения, поэтому требуется задать элемент типа «Spring» (пружина) – упругий элемент, позволяющий задать кривую жесткости. В расчете на динамические нагрузки с помощью элемента «Spring» осевая жесткость подшипника задается графиком зависимости силы приложенной нагрузки от перемещения. Таким образом, в анализе учитываются радиальная и осевая жесткости подшипников.

В качестве граничных условий для исследуемого модуля используется закрепление с ограничением перемещения и поворотом по всем осям в местах, предусмотренных конструкторской документацией на изделие. Общий вид полученной КЭМ показан на рис. 3.

Для корпусных деталей редукторной сборки используется материал ВТ14. Для элементов зубчатого зацепления в волновой и планетарной передачах используется сталь 95Х18. Для деталей двигателя применяется АМг6. Модуль упругости и коэффициент Пуассона материалов, используемых в расчете, представлены в табл. 1.

Том 7

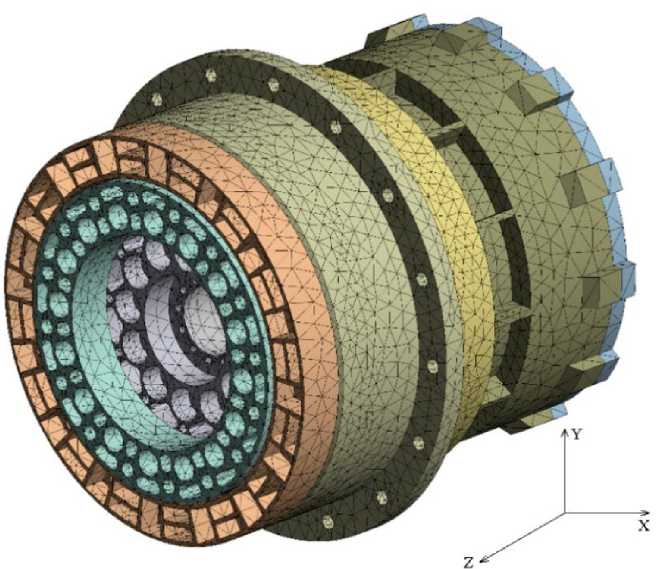
Рис. 3. Общий вид КЭМ УММ-ИП

Вибрационные нагрузки

Таблица 2

Нагрузки	По всем осям координат
	Частота, Гц	Уровень, м/с2 (g)
Синусоидальные вибрации	5–10	±10 мм
	10–20	от ±39,24 (4) до ±196,2 (20)
	20–100	±196,2 (20)
Случайная вибрация	20–100 100–300 300–360 360–500 500–2000	+6 дБ/окт 0,8 g2/Гц –12 дБ/окт 0,4 g2/Гц –12 дБ/окт
Среднеквадратическое значение ускорения, g	18,6

Таблица 1

Материал	95Х18	АМг6	ВТ14
Модуль упругости, Па	2∙1011	0,71∙1011	1,1∙1011
Коэффициент Пуассона	0,3	0,33	0,36

Свойства материалов

Перед проведением динамического анализа проводится статический анализ без задания дополнительных нагрузок для решения контактной задачи в местах зацепления зубчатых передач и пересчета коэффициентов матрицы жесткости, что определяет преднагруженное состояние модели. Пересчет коэффициентов матрицы жесткости необходим, так как в дальнейшем используется линейная динамика, при которой жесткость остается постоянной.

Проводимый далее динамический анализ заключается в определении собственных частот (модального анализа), которые отражают отклик конструкции на внешние механические воздействия, и анализе воздействия на конструкцию синусоидальной и случайной вибраций.

По техническому заданию УММ не должен иметь конструктивных элементов и узлов с резонансными (собственными) частотами ниже 50 Гц.

При проведении динамического анализа величины нагружающих воздействий устанавливались в соответствии с техническими требованиями стойкости к механическим воздействиям, приведенным в табл. 2.

При проведении анализа на воздействие синусоидальной вибрации выполняли три исследования с разными диапазонами частоты и амплитуды воздействия по трем осям координат при помощи модуля Harmonic Response. При анализе случайной вибрации проводилось одно исследование по трем осям с помощью модуля Random Vibration. Расположение осей системы координат для УММ-ИП показано на рис. 3.

2.    Описание результатов расчетов

Полученные результаты рассматриваются при 3σ, что соответствует вероятности 99,72 %. Максимальные значения напряжений и перемещений, полученные при проведении статического анализа, сконцентрированы на гибком колесе волновой передачи. Полученное преднагруженное состояние применяется как начальное состояние для динамического расчета.

Модальный анализ

Задачей модального анализа является поиск первых 20 колебательных мод (собственных частот). Полученные частоты приведены в табл. 3.

Значения собственных частот передаются в модуль Random Vibration для дальнейшего анализа воздействия случайной вибрации на конструкцию УММ-ИП.

Анализ влияния синусоидальной вибрации

В ходе анализа влияния синусоидальной вибрации было выявлено, что нагрузка в 1g оказывает минимальное влияние на исследуемый УММ-ИП, в связи с чем графики его амплитудночастотной характеристики (АЧХ) имеют линейный вид при данной нагрузке (рис. 4 а ).

При синусоидальной вибрации на частоте 10–20 Гц и увеличении значения ускорения от 4 до 20g максимальный отклик наблюдается при воздействии ускорения 20g (рис. 4 б ).

Таблица 3

Номер моды	Частота, Гц	Номер моды	Частота, Гц
1	605,32	11	3552
2	861,36	12	3621,2
3	934,76	13	3686,8
4	2599,0	14	3710,1
5	2606,4	15	3877,8
6	2867,7	16	4387,8
7	2967,3	17	4700,5
8	3123,8	18	4798,2
9	3160,4	19	4868,9
10	3354,7	20	5017,9

Собственные частоты

При воздействии нагрузки величиной 20g на частоте 20-100 Гц максимальный отклик наблюдается на частоте 100 Гц (рис. 4 в ).

Значения максимального отклика по каждой оси были зафиксированы при совпадении осей нагрузки и отклика. Графики АЧХ для трех диапазонов представлены на рис. 4.

Анализ влияния случайной вибрации

При воздействии случайной вибрации максимальные напряжения сконцентрированы в местах зубчатого зацепления планетарной передачи, как показано на рис. 5, и по осям X, Y составляют 32 МПа, по оси Z – 18 МПа.

В состав исследуемого модуля входит вращающийся трансформатор, для правильной работы которого необходимо обеспечить воздушный зазор между статором и ротором. Несоблюдение воздушного зазора в 1 мм является критичным для точности позиционирования УММ-ИП. В ходе анализа было выявлено, что максимальное перемещение составляет 0,044 мм при воздействии нагрузки по оси Y, следовательно, радиальное перемещение статора и ротора не превышает заданного конструктивного значения. Эпюра распределения перемещений представлена на рис. 6.

Заключение

Разработана конечно-элементная модель УММ-ИП с учетом радиальной и осевой жесткости подшипников. По результатам статического анализа изучены контактные напряжения в зуб-

■ОсьХ

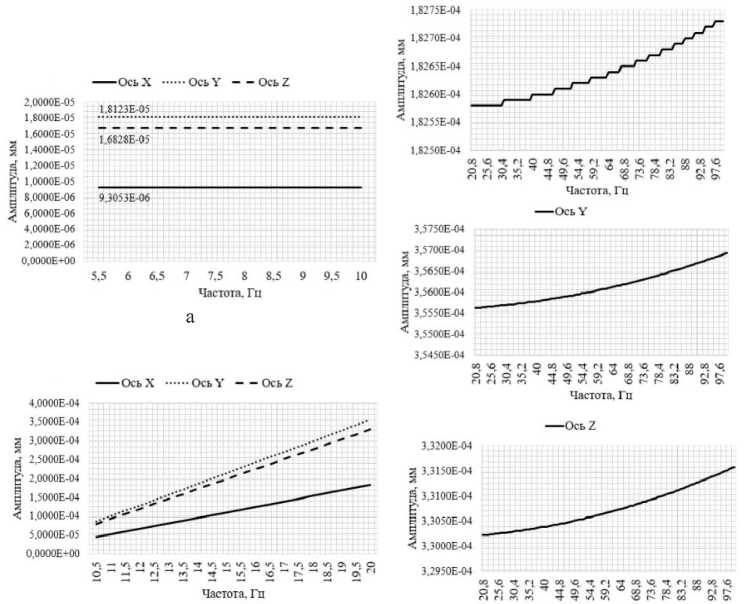
б

в

Рис. 4. а – график АЧХ по осям Х, Y, Z при нагружении ускорением 1g по осям X, Y, Z на частоте 5–10 Гц; б – график АЧХ по осям Х, Y, Z при нагружении ускорением от 4 до 20 g по осям X, Y, Z на частоте 10–20 Гц; в – график АЧХ по осям Х, Y, Z при нагружении ускорением 20g по осям Х, Y, Z на частоте 20–100 Гц

Том 7

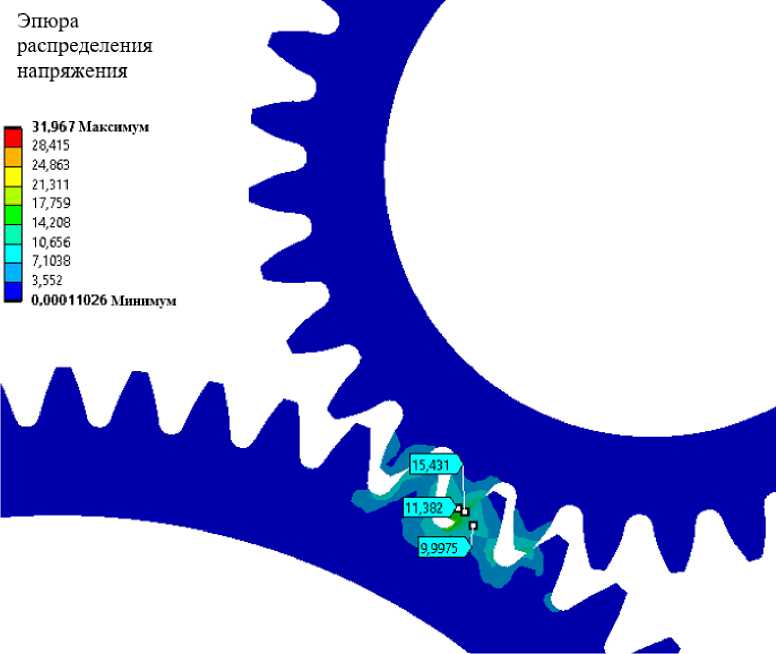
Рис. 5. Распределение напряжения в месте зубчатого зацепления в планетарной передаче по оси X

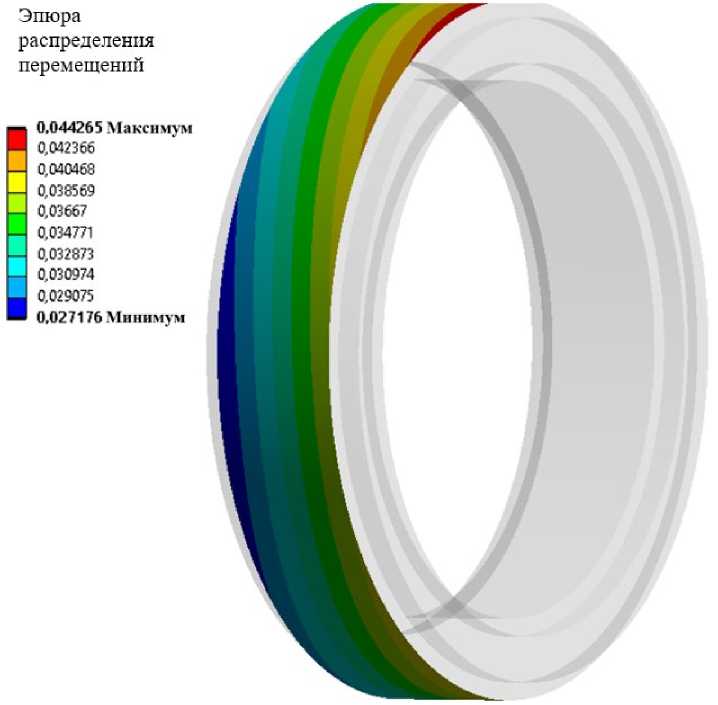
Рис. 6. Эпюра распределения перемещений на детали ротора

чатом зацеплении и скорректированы коэффициенты матрицы жесткости. Проведен анализ динамических нагрузок для исследования стойкости к механическим воздействиям – синусоидальным и случайным вибрационным нагрузкам.

По результатам динамического анализа УММ-ИП не имеет собственных частот ниже 50 Гц. По анализу графиков амплитудночастотной характеристики для трех диапазонов частот УММ-ИП является стойким к воздействию синусоидальной вибрации. Полученные данные о перемещениях и возникающих напряжениях в пределах трех среднеквадратичных отклонений, о распределении напряжений по конструкции при воздействии случайной вибрации позволяют сделать вывод, что УММ-ИП является стойким к воздействию случайной вибрации. Воздушный зазор между статором и ротором вращающегося трансформатора не нарушается под действием случайной вибрации, обеспечивается исправная работа элементов УММ-ИП.

Работа выполнена в рамках проекта «Создание высокотехнологичного импортозамещающего производства универсальных многофункциональных мехатронных модулей, предназначенных для обеспечения работы исполнительных систем трансформируемых конструкций объектов авиационно-космической техники, обеспечивающей освоение и использование Мирового океана,

Арктики и Антарктики» в БГТУ «ВОЕНМЕХ» им. Д. Ф. Устинова при финансовой поддержке Министерства науки и высшего образования Российской Федерации (соглашение № 075–11– 2021–057 от 28.06.2021) в соответствии с постановлением Правительства РФ от 09.04.2010 № 218.