Особенности численного моделирования упругопластического выпучивания полусферических оболочек при нагружении жестким индентором

PNRPU MECHANICS BULLETIN

Для упругопластических сферических оболочек при сжатии, потере устойчивости и последующем закритическом деформировании характерна близкая к билинейной зависимость силы сопротивления от прогиба. Благодаря этому они хорошо поглощают (адсорбируют) энергию внешнего динамического воздействия и представляют значительный интерес как демпфирующий элемент при проектировании современных противоударных конструкций.

Результаты теоретических и экспериментальных исследований упругопластического выпучивания сферических оболочек при различных условиях нагружения представлены в [1–14]. Рассмотрены задачи упругопластического выпучивания сегментов сферических оболочек [1–3] и замкнутых сферических оболочек [4] при нагружении равномерным внешним давлением. Отмечено, что учет пластических деформаций приводит к существенному снижению критической нагрузки. В [5, 6] представлен обзор методов и результатов теоретических и экспериментальных исследований устойчивости тонкостенных конструкций. Производится анализ выпучивания сегментов пологих сферических оболочек при квазистатиче-ском сжатии локальными нагрузками, приложенными по периметру сегмента. Изучены разнообразные аспекты влияния локальных конструктивных дефектов на устойчивость оболочек. Показано, что угол обхвата ложемента существенно влияет на форму волнообразования. В [7] проведен экспериментальный и численный анализ осесимметричного упруго- пластического выпучивания полусферических оболочек (26 < R/h < 45) при сжатии между двумя плитами. В [8] приводятся результаты экспериментальных и теоретических исследований предельных состояний стальных полусферических оболочек с различными геометрическими параметрами при локальном контактном нагружении недеформируемыми инденторами различной формы. В [9, 10] представлены результаты конечно-элементного анализа нелинейного деформирования алюминиевых и стальных полусферических оболочек при осевом ударном и квазистатическом нагружениях. Исследовано влияние геометрических параметров и упругопластических характеристик конструкционных материалов на деформирование оболочек. В [11] в осесимметричной постановке рассмотрена задача упругопластического выпучивания свинцовой сферической оболочки в алюминиевом скафандре под действием импульса перегрузки. В [12] излагается процедура калибровки теоретических результатов (критических нагрузок) на основании экспериментальных данных.

С развитием математических моделей, вычислительной техники, численных методов и программных систем появились новые возможности решения задач устойчивости упругопластических конструкций в геометрически нелинейной постановке как неидеальных систем с начальными несовершенствами формы при сложных нагружениях. При этом вместо критических бифуркационных нагрузок определяются предельные нагрузки и соответствующие формоизменения конструкций. Для численного решения подобных квази-статических задач в теории упругости хорошо разработан метод продолжения по обобщенному параметру нагружения [13]. Для упругопластических задач этот метод неэффективен и малопригоден, особенно при решении контактных задач, ввиду зависимости решения от истории нагружения, которое фактически не предоставляет свободы выбора оптимального параметра нагружения с целью регуляризации задачи в предельных точках интегральной зависимости нагрузка-перемещение. В связи с этим для исследования процессов деформирования и оценки предельных состояний упругопластических тел при неоднородных напряженно-деформированных состояниях, сложных нагружениях и немалых формоизменениях получила применение динамическая формулировка задачи с использованием в качестве параметра нагружения модифицированного времени [1–3]. В квазистатических задачах роль регуляризатора численного решения выполняют инерционные члены, вклад которых регулируется выбором соответствующей скорости нагружения и ее реверсом при разгружениях. Отметим, что динамическая постановка задачи в сочетании с явной схемой интегрирования по времени позволяет весьма эффективно моделировать закритическое поведение и контактное взаимодействие упругопластических элементов конструкций при квазистатическом нагружении [1–3, 14].

Ниже приводятся результаты численного исследования квазистатического выпучивания упругопластических полусферических оболочек при вдавливании жестких инденторов в динамической постановке [2, 14]. Решение задачи основано на моментной схеме метода конечных элементов и явной конечно-разностной схеме интегрирования по времени типа «крест» [1, 2]. Результаты расчетов сопоставляются с экспериментальными данными.

1.    Определяющая система уравнений и метод решения

Деформирование оболочки описывается в переменных Лагранжа с позиций механики сплошных сред [15–19]. Наряду с общим базисом X = [ X ₁ X ₂ X ₃] введем местную (сопутствующую) систему координат x = [ x ₁ x ₂ x ₃] с направляющими косинусами n _ij :

Xi = n j X j ,¹ , j = 1,3                                        (!)

(по повторяющимся индексам ведется суммирование). Здесь х ₃ - координата, отсчитываемая от срединной поверхности оболочки и нормальная к ней, x ₁, x ₂ - ортогональны к х ₃. Деформации поперечного сдвига предполагаем малыми, что позволяет считать местный базис ортогональным в течение всего процесса деформирования. Компоненты тензора скоростей деформаций в местном базисе s j выражаются через компоненты e j скорости деформаций в общем базисе:

^s j = n m n jk e mk ,                                           ⁽²⁾

которые определяются в метрике текущего состояния,

t ej= (Uj Uj^Q, (i, j = 1,3) X= X| t=0 + J Utdt.                (3)

В (2) U i - перемещения в общей декартовой системе координат Х ; индекс после запятой означает частную производную по соответствующей пространственной переменной, точка над символом - частную производную по времени t .

Уравнение движения выводится из баланса виртуальных мощностей [15,16,19]:

J o j 5s ij dV + J p U i 5 U i dV = J P i 5 Ud y+ J P q 5 Ud y ( i , j = □),           (4)

ΩΩ    ΓpΓq где Ui - компоненты вектора скорости перемещения в общей декартовой системе координат Х; о у - компоненты тензоров напряжений Коши; р - плотность; Piq - контактное давление; Pi - распределенная нагрузка; Q - исследуемая область; Г q - поверхность контакта; Г p -зона действия внешнего давления; 5s j, 5 Ui - вариации sj, Ui (на поверхности с заданными кинематическими граничными условиями 5 Ui = 0); точка над символом означает частную производную по времени t; по повторяющимся индексам ведется суммирование.

Упругопластическое деформирование материала описывается соотношениями теории течения [1, 20, 21].

V

° ij ^о _у + ° ⁵ , _д V =— 3 к s V , s V =ё _/7 /3,

S=s ij -s V 5 ij -s p , s p = 0 , о ij = 2 G s,                            (5)

t sp = Xdf/doj, f = ojoj-3o2 =0; от = от(x), x = Jsipdt.

Здесь o j , s j , о ^v , s ^v - девиаторные и шаровые компоненты тензоров напряжения и скоростей деформаций; s ^p - скорости пластических деформаций; G , К - модули сдвига и объемного сжатия; 5 j - символы Кронекера; f - поверхность текучести Мизеса; о т -динамический предел текучести; X - параметр, тождественно равный нулю при упругом деформировании и определяемый при упругопластическом деформировании из условия прохождения мгновенной поверхности текучести через конец вектора догрузки.

На контактной поверхности формулируются условия непроникания по нормали и свободного скольжения вдоль касательной к поверхности контакта:

U n = Un , qn = qn , qi = qi = 0 , i = T1, T2 , где n, T1, t2 - единичные векторы локального, ортогонального базиса, n - вектор нормали к поверхности контакта, т1, т2 ортогональны n; нижний индекс i означает проекцию вектора на оси подвижной системы координат, верхними индексами 1 и 2 обозначены номера соответствующих подобластей, поверхности которых находятся в контакте. Определяющая система уравнений (1)–(4) дополняется кинематическими граничными и начальными условиями.

Для дискретизации определяющей системы уравнений применяются моментная схема метода конечных элементов и явная конечно-разностная схема типа «крест» [19, 22– 25]. Оболочка заменяется лагранжевой сеткой, состоящей из 8-узловых конечных элементов (КЭ). В узлах сетки определяются ускорения { U } , скорости { U } и перемещения { U } в общей системе координат { X } = { X 1 X ₂ X 3 } T . Предполагается, что деформации поперечного сдвига в конечных элементах малы, а смещения и углы поворота КЭ как жесткого могут быть большими. В каждом конечном элементе вводится локальный базис { x } = { x 1 x ₂ x 3 } T (1), отслеживающий его вращение как жесткого целого пошаговым пересчетом направляющих косинусов осей [1, 25, 26]. Конечный элемент с помощью полилинейного изопараметрического преобразования отображается на куб - 1 < 5 i <  1 ( i = 1, 3) :

x - = E x k N ( ^ 1 5 2 5 3 ) , N = (1 +5 1 / ^ k X1 + 5 , / 5 k )(1 +5 з / 5 k )/8 ,           (7)

k = 1

где xk, 5k — координаты узлов в базисах x, 5; Nk — функции формы. Компоненты скорости деформаций гу в КЭ аппроксимируются линейными функциями a ij = a 0 + a j 51 + a 2 52 + a 3 5з,                                     (8)

где a 0 - значения компонент скорости деформаций в центре КЭ (безмоментные составляющие), а a k = da j / d5 _k = const — их градиент (моментные составляющие). Чтобы не завышать сдвиговую жесткость элемента, в (6) учитываются только компоненты a j, соответствующие изгибающим и крутящим моментам в теории оболочек [24].

С применением формул численного интегрирования [17, 18] напряжения, определенные в локальном базисе, заменяются статически эквивалентными узловыми силами, которые проецируются в общую систему координат. После замены интегрирования по области Q суммированием по элементам получим дискретный аналог уравнений движения

[ M ]{U} = { F },                                     (9)

где [M] - диагональная матрица масс; {Uj}, {F} - векторы, составленные из ускорений узлов КЭ-сетки и результирующих узловых сил в общей системе координат. Система обыкновенных дифференциальных уравнений (9) интегрируется по явной конечноразностной схеме типа «крест».

Численная схема для определения контактного давления и статически эквивалентных ему узловых сил приведена в [23].

Конечно-элементная методика [19, 22, 23] реализована в рамках вычислительной системы (ВС) «Динамика-3», аттестованной в научно-техническом центре по ядерной и радиационной безопасности (регистрационный паспорт аттестации ПС № 325 от 18.04.2013) и Госстандарте РФ (сертификат соответствия Госстандарта России № РОСС RU.ME20.H00338).

2.    Результаты исследований

На основе изложенной выше методики и ВС «Динамика-3» выполнен расчет упругопластического деформирования и выпучивания полусферической стальной оболочки

( R = 3,85 см, R/h = 48,125, p = 7,8г/см³, Е = 150 ГПа, ц = 0,33, диаграмма деформирования приведена на рис. 1), расположенной на неподвижной плите при квазистати-ческом вдавливании недеформируемого индентора, имеющего вид цилиндрической оболочки ( R = 2,5 см, R/h = 5) с продольными вырезами в области контакта, количество N которых варьировалось (рис. 2, а , б ). Размеры опорных элементов инденторов при этом не менялись. Скорость вертикального смещения индентора 1 м/с.

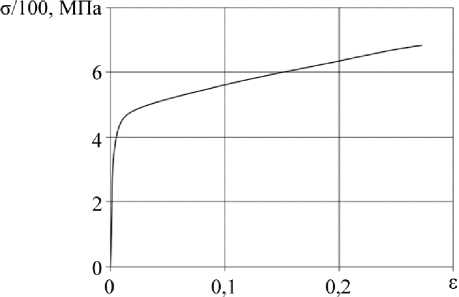
Рис. 1. Диаграмма деформирования

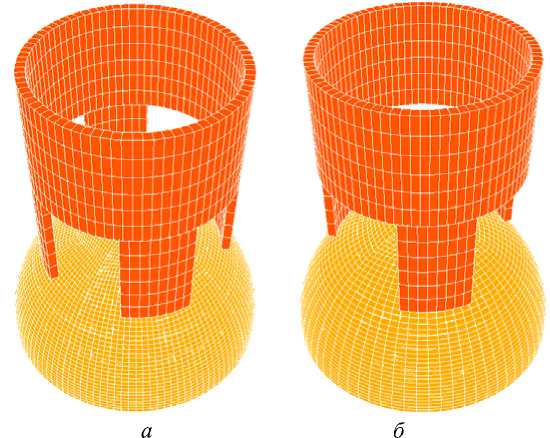
Рис. 2. Формы инденторов и конечно-элементные сетки расчетной области: а – N = 4; б – N = 3

Численное исследование проводилось на сетках с одним слоем конечных элементов по толщине оболочки. Количество конечных элементов сетки оболочки в расчетах было равным 4800. Результаты решения задачи приведены на рис. 3–5.

На рис. 3, а , б представлены графики F ( u ) изменения контактной силы в зависимости от смещения инденторов, изображенных на рис. 2, а , б соответственно. Сплошной, пунктирной и штриховой линиями отмечены результаты эксперимента [8] и расчетов в квазистатической и динамической постановке с применением вычислительных систем ABAQUS [8, 27] и «Динамика-3» соответственно. На рис. 3, в сравниваются графики зависимости F ( u ), полученные на основе ВС «Динамика-3» для инденторов при N = 4 и N = 3. Остаточные формы полусферической оболочки в расчете и натурном эксперименте [8] для первого варианта задачи ( N = 4) представлены на рис. 4. Распределение интенсивностей пластических деформаций в оболочке, полученное с применением вычислительной системы «Динамика-3», изображено

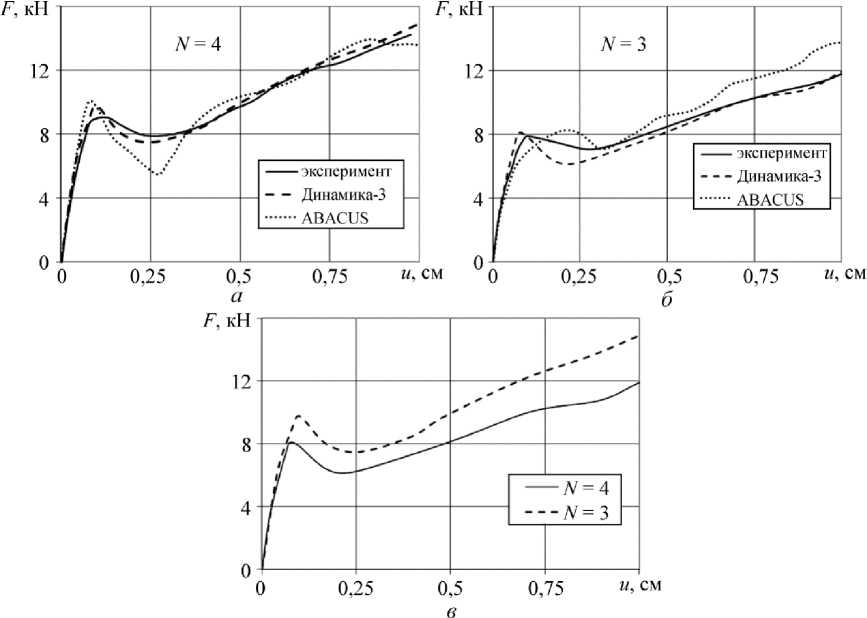
Рис. 3. Зависимость контактной силы от смещения индентора

а

б

Рис. 4. Остаточная форма оболочки для первой задачи ( N = 4): а – эксперимент; б – ВС «Динамика-3»

б

а

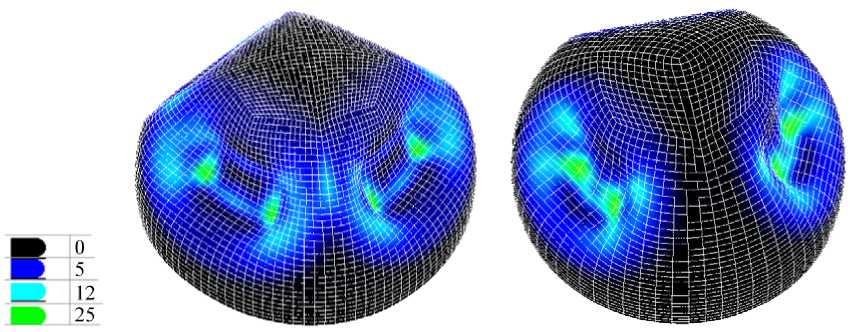
Рис. 5. Остаточное распределение интенсивности пластических деформаций (%) в оболочке: а – N = 4; б – N = 3

на рис. 5 на момент окончания нагружения. В табл. 1 приведены максимальные значения параметра Одквиста χ , сдвиговых деформаций ε 12 в срединной поверхности оболочки, а также деформаций поперечного сдвига ε 23 , ε 31 .

Таблица 1

Максимальные деформации (%)

N	χ	ε 12	ε 23	ε 31
4	25	8,3	2,9	2,6
3	23	7	2,5	2

Как видно из рис. 4, 5, полусферическая оболочка в процессе нагружения претерпевает значительные локальные формоизменения, характеризуемые большими смещениями и углами поворота конечных элементов как жесткого целого. Так, углы поворота конечных элементов в зоне вмятин достигают 70 градусов. Изгибные деформации оболочки, по расчетным данным, не превышают 25 %. Максимальное значение деформаций поперечного сдвига оболочки составляют 3 %, а максимальные сдвиговые деформации срединной поверхности оболочки 8,3 %.

В табл. 2 приведены расчетные и экспериментальные значения критической нагрузки для рассмотренных вариантов задачи.

Таблица 2

Критические значения нагрузки (кН)

	Расчет (ВС «Динамика-3»)	Эксперимент
N = 4	9,7	9,02
N = 3	8,1	7,9

Снижение площади контакта оболочки и индентора на 25 % при уменьшении числа продольных вырезов в цилиндрической оболочке (см. рис. 2) в расчетах и экспериментах приводит к уменьшению критического значения нагрузки примерно на 15 %.

При кинематическом закритическом нагружении нет скачкообразного динамического перехода на закритическую ветвь деформирования. На всех этапах нагружения, в том числе и на падающей ветви деформирования после достижения критической нагрузки, оболочка находится в устойчивом равновесном состоянии. Образование локальных вмятин сопровождается временным снижением контактной силы. При дальнейшем расширении локальных вмятин сила сопротивления оболочки внедрению индентора возрастает за счет упрочнения материала и увеличения жесткости оболочки (см. рис. 3).

Проведенные расчеты свидетельствуют о достаточной эффективности применения динамического подхода к исследованию предельных состояний упругопластических оболочек при квазистатических нагружениях и больших формоизменениях. ВС «Динамика-3» с удовлетворительной для инженерной практики точностью описывает исследуемый процесс. Так, рассогласование графиков зависимости контактной силы от смещения нагружающего устройства, полученных расчетным путем на основе ВС «Динамика-3» и экспериментально, на закритической стадии деформирования оболочки не превышает 5 %. Остаточные формы оболочки в расчете и эксперименте также соответствуют друг другу. Численные результаты решения задачи с применением ВС «Динамика-3» в динамической постановке в целом лучше согласуются с экспериментальными данными, чем результаты, полученные на основе ABAQUS в квазистатической постановке.

Выводы

Сопоставление результатов расчетов на основе ВС «Динамика-3» с экспериментом показало, что при малых деформациях поперечного сдвига и больших углах поворота применение моментной схемы метода конечных элементов с определением скоростей деформаций и напряжений в местном вращающемся базисе, определяемом изменением геометрии оболочки, обеспечивает приемлемую точность вычислений при использовании явной конечно-разностной схемы интегрирования типа «крест» с малыми шагами по времени, что соответствует данным расчетно-экспериментальных исследований [28]. Относительно грубая дискретизация геометрии оболочки стала возможной благодаря принятой аппроксимации скоростей деформаций и напряжений в моментной схеме МКЭ [19, 22, 23], которая является, по существу, численной реализацией шестимодального варианта теории оболочек типа Тимошенко [24] и позволяет моделировать динамику тонкостенных оболочек на сетках с одним слоем элементов по толщине.

Исследование выполнено за счет гранта Российского научного фонда (проект № 16-19-10113).