Особенности фазирования электрооптических поверхностей

Дискретные оптические элементы (ДОЭ), в т.ч. дифракционные оптические элементы, широко используются в качестве фокусаторов лазерного и широкополосного оптического излучения в произвольную область, корректоров волнового фронта, выполняют функции спектрального и амплитудного преобразования [1,2]. К настоящему времени сформированы обобщенные теоретические модели и методы расчета и синтеза ДОЭ со статическими параметрами, имеющие достаточно высокую практическую точность [2].

Одним из путей развития элементной базы оптики является создание перестраиваемых оптических элементов с управляемыми (адаптивными) оптическими характеристиками и синтезируемой апертурой, что позволит расширить функциональность элементов и устройств на их основе.

Разработка ДОЭ на периодических, в том числе дифракционных структурах (решетках), в силу малой величины электрооптического эффекта [3] требует оптимального сочетания параметров электрооптического материала (ЭОМ), взаимной пространственной ориентации оптических осей ЭОМ, светового потока и силовых линий электрического поля.

Проведенный анализ показывает, что даже для простых структур ДОЭ нельзя заранее предсказать эффективность выбранного конструктивного варианта реализации ДОЭ и применяе-

мого ЭОМ. В тоже время введение ряда критериев позволяет оценить как эффективность использования электрических полей в ДОЭ, так и эффективность пространственной ориентации оптических осей ЭОМ и световых потоков.

ФУНКЦИОНАЛ

ПРЕИМУЩЕСТВЕННОГО ТИПА ЭЛЕКТРООПТИЧЕСКОГО ЭФФЕКТА

Для упрощенного анализа ДОЭ с периодической структурой разобьем ДОЭ на ряд элементарных базовых оптических элементов (ЭБОЭ) таким образом, чтобы добавление очередного ЭБОЭ к группе уже сформированных ЭБОЭ не влияло на характеристики последних. Для оценки типа распределения электрического поля в ЭБОЭ и выбора соответствующего типа электрооптического введем понятие функционала G преимущественного типа электрического поля в ЭБОЭ:

G =

J ^j [| F^x ( x , y )| - | F^y ( x , y )|] dxdy 00

координат x, y; n(x,y) – координатная зависимость коэффициента преломления ЭОМ.

В частности, для ДОЭ на основе дифракционных решеток, в зависимости от отношения периода решетки к толщине резонансного слоя наблюдается существенное перераспределение продольной и поперечной составляющих электрооптического эффекта (рис. 1).

На рис. 1 вектор А указывает направление распространения световой волны.

На рис.2 величины функционала G от отношения .

d

Из рис.1,2 видно, что при a = 8 доля Ex d                       i,j компоненты электрического поля доминирует и составляет величину порядка 90%, а электрооп тический эффект в этом случае поперечный.

-

a

При d ⁼ 1,2

доля Eix, j компоненты элект- рического поля уменьшается до величины порядка 60%, а электрооптический эффект в этом случае преимущественно поперечный с долей продольной компоненты порядка 30%.

a

При d ⁼ 0,3

доля Eix, j компоненты элект- рического поля уменьшается до величины порядка 50%, а электрооптический эффект в этом случае смешанный с долей продольной компоненты порядка 50%.

Вывод. Устанавливая классификационную величину функционала G например по уровням

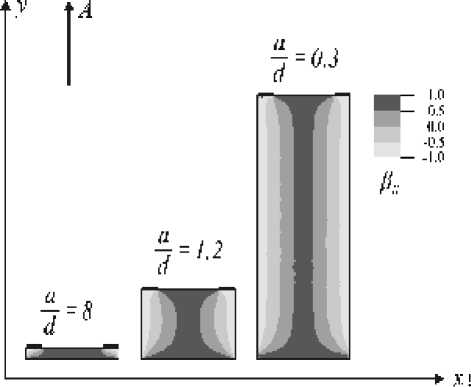
Рис. 1. Распределение проекций вектора напряженности электрического поля

0,1 и 0,9 (рис. 2), получим три зоны преимущественного типа электрооптического эффекта: I – преимущественно поперечный электрооптический эффект; II – смешанный (промежуточный) электрооптический эффект; III – преимущественно продольный электрооптический эффект.

Определение. Под фазированием оптической поверхности будем понимать создание требуемого одно- или двумерного распределения фазы Φ _sur f светового пучка, пересекающего данную поверхность.

В общем случае световая волна может распространяться перпендикулярно фазируемой поверхности или пересекать ее под некоторым углом.

Поскольку фактически получаемая фазовая функция Φ f может не совпадать с целевой Φ _surf , для количественной характеристики сходимости Φ f и Φ _surf можно ввести интегральную Δϕ _int ошибку:

Δϕ _int = ∫ ( Φ _surf - Φ _f ) ² dS ,

S где S – фазируемая поверхность. В этом случае требование к формируемой фазовой функции Φf должно удовлетворять критерию минимума среднеквадратичной ошибки:

Δϕ _int → min

Для создания фазовой функции электрооптически активной поверхности можно предложить несколько методов, основанных на управлении распределением электрического поля в объеме ЭОМ, выборе определенной ориентации ЭОМ, а также их комбинации.

Для описания пространственных электрических полей и оптических осей ЭОК введем понятия системы координат кристалла (СКК) и электрического поля (СКЭП).

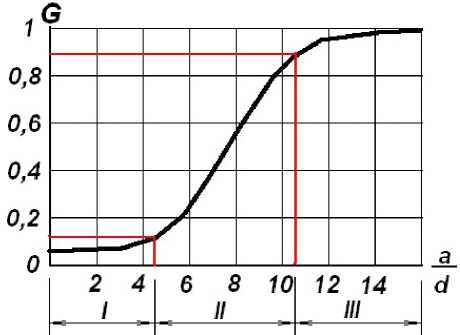
Рис. 2. Зависимость величины функционала G

a в зависимости от отношения d

a от отношения d

Координатной системой СКК служит ортогональный базис векторов x₂y₂z₂ , параллельных оптическим осям ЭОК, причем для рассматриваемых ниже одноосных кристаллов вектор z₂ полагается совпадающим с осью оптической анизотропии.

Система СКЭП является фиксированной системой координат с ортогональными направляющими x₁y₁z₁ , в которой задаются величины и направления внешних электрических полей, геометрия и ориентация управляющих электродов, направление распространения световой волны, т.е. в СКЭП задается большинство исходных данных задачи. В общем случае оси x₂y₂z₂ СКК могут быть как параллельными координатным осям x₁y₁z₁ СКЭП, так и ориентированными под произвольными углами.

ВЛИЯНИЕ ОРИЕНТАЦИИ ВЕКТОРА

НАПРЯЖЕННОСТИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ НА ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ ЭЛЕКТРООПТИЧЕСКОГО МАТЕРИАЛА ДЛЯ ВОЛН ОСНОВНЫХ ПОЛЯРИЗАЦИЙ

Данный частный случай характеризуется тем, что сочетание элементов матрицы электрооптических коэффициентов r_ij и действующих электрических полей E_k таково, что в уравнении эллипсоида показателей преломления коэффициенты при переменных x₂, y₂, z₂ зависят от двух или более составляющих E_k . Это позволяет, используя методы независимого регулирования по каждому из векторов электрического поля E_x2, E_y2, E_z2 путем выбора ориентации кристалла, поляризации световой волны , изменять показатель преломления в объеме ЭОК в соответствии с целевой функцией.

В качестве примера рассмотрим изменение показателей преломления x₂, y₂ – поляризованных волн в ниобате лития, ориентированного так, как это показано на рис. 3. Электрическое поле создается с помощью двух протяженных электродов и включает составляющие E_x1 = E_y2 и E_y1 = E_z2 (оси x₂,y₂,z₂ СКК параллельны осям z₁,x₁,y₁ СКЭП). Световая волна распространяется вдоль оси z₂ || y₁ .

Изменение эллипсоида показателей преломления в плоскости x₂y₂ примет вид:

л

r 22 E y 2

+ ^r 13 E z 2 x 2 ² +

\

+   ₂ + ^r 22 E y 2

I n 0

+ ^r 13 E z 2 У 2 ² = ¹

или в системе СКЭП:

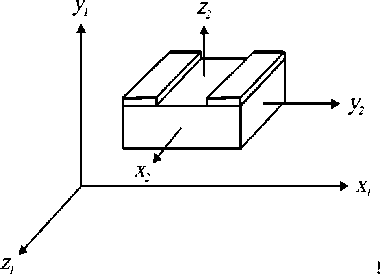
Рис. 3. Ориентация оптических осей кристалла в СКЭП

f 1

"У - ^r22 E x1 + ^r13 E y 1 z 1 +

V n 0

+ — + Г— E xi + r ig E yi x i = ¹

V n 0

Показатели преломления для x₂, y₂ -поляри-зованных волн будут равны:

n x 2 = n 0 + 2 n 0 ^r 22 E y 2 ^- - n 0 ^r13 E z 2 ;

n y 2 = n 0 ^- 2 n 0 ^r22 E y 2 ^- ^ n 0 ^r 13 E z 2 . (1)

Из выражений (1) следует, что фазовая функция светового пучка в выходном межэлектродном промежутке формируется двумя составляющими электрического поля – E_y2 и E_z2 , которые являются соответствующими проекциями полей E_x1 , E_y1 СКЭП на оси симметрии кристалла x₂,y₂,z₂ (рис. 3). Поэтому, путем выбора ориентации ЭОК, возможно изменение вклада каждой составляющей электрического поля на показатели преломления материала. Например, вращение СКК вокруг оси z₂ уменьшит электрическое поле E_y2 и увеличит составляющую E_x2 при неизменной величине E_z2 . Таким образом, с использованием определенного среза ЭОК, возможно формирование требуемого фазового распределения световой волны на выходе структуры.

Для рассмотренного варианта фазирования необходимы, по крайней мере, две составляющие электрического поля, с целью изменения их соотношения в величине фазового набега, а также наличие определенных ненулевых электрооптических коэффициентов r_ij . Для простого случая ориентации осей симметрии кристалла параллельно осям СКЭП данные требования оформлены в виде табл. 1.

Переход от векторов x₁,y₁,z₁ к x₂,y₂,z₂ или от E_x1,E_y1,E_z1 к E_x2,E_y2,E_z2 в данном случае задается простым соответствием осей СКК и СКЭП, однако

Таблица 1. Требования к матрице электрооптических коэффициентов.

Направление световой волны	Составляющие электрического поля в СКК	Поляризация световой волны	Электрооптические коэффициенты	Класс симметрии кристалла
z 2 ||y 1	Ez 2 , Ex 2	x 2 y 2	r11, r13 r21, r23	1,m,3,3m 1,m,3,3m
	Ez 2 , Ey 2	x 2 y 2	r12, r13 r22, r23	1,3,3m 1,3,3m
y 2 ||y 1	Ey 2 , Ex 2	x 2 z 2	r11, r12 r31, r32	1,m,3, 6 1,m,3
	Ey 2 , Ez 2	x 2 z 2	r12, r13 r32, r33	1,3,3m 1,3m
x 2 ||y 1	Ex 2 , Ey 2	y 2 z 2	r21, r22 r31, r32	1,m,3, 6 1,m
	Ex 2 , Ez 2	y 2 z 2	r21, r23 r31, r33	1,m,3m 1,m

при произвольной ориентации СКК в СКЭП должен осуществляться через линейное преобразование базисных векторов в пространстве.

Вывод: для реализации рассмотренного типа фазирования оптической поверхности ЭОК должен иметь как минимум 2 ненулевых элемента, по крайней мере, в одной из первых трех строк матрицы электрооптических коэффициентов. Это обстоятельство ограничивает номенклатуру материалов, не позволяет выбрать материалы с высокими значениями электрооптических коэффициентов.

ВЛИЯНИЕ ОРИЕНТАЦИИ ВЕКТОРА

НАПРЯЖЕННОСТИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ НА ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ ЭЛЕКТРООПТИЧЕСКОГО МАТЕРИАЛА ДЛЯ ВОЛН ПРОМЕЖУТОЧНЫХ ПОЛЯРИЗАЦИЙ

Данный частный случай характеризуется тем, что сочетание элементов матрицы электро оптических коэффициентов r_ij и действующих электрических полей E_k таково, что в уравнении эллипсоида показателей преломления при наличии внешнего электрического поля возникают ненулевые коэффициенты как при переменных x₂, y₂, z₂ , так и при слагаемых x₂ y₂, x₂z₂ и т.п, причем изменение показателя преломления для волн x₂- , y₂- , z₂- и x₂y₂- , x₂z₂- и т.п. поляризаций происходит под действием различных составляющих поля E_x2, E_y2, E_z2 .

Влияние управляющего поля будет выражаться в одновременном изменении оптической индикатрисы вдоль основных осей x₂, y₂, z₂ и новых (наведенных) осей x₃, y₃, z₃ эллипсоида показателей преломления. Это позволяет использовать влияние векторов электрического поля

E_x2, E_y2, E_z2 на показатель преломления в объеме ЭОК путем выбора ориентации кристалла и поляризации световой волны. Принципиальным отличием от предыдущего частного случая будет использование световых волн с промежуточной поляризацией типа x₂y₂- , x₂z₂- и т.п., либо поляризованных вдоль новых оптических осей.

В качестве примера рассмотрим изменение показателей преломления x₂z₂ – поляризованных волн в ниобате лития, ориентированного так, как это показано на рис. 4. Электрическое поле создается с помощью двух протяженных электродов и включает составляющие E_x1= E_x2 и E_y1=E_y2 (оси z₂,y₂,x₂ СКК параллельны осям z₁, y₁,x₁ СКЭП). Световая волна распространяется вдоль оси y₂ || y₁ .

Изменение эллипсоида показателей преломления в плоскости x₂z₂ примет вид:

(

I n 02

/

2         1       2

r 22 E y 2 x 2 +    2 z 2 + ² z 2 x 2 ^r 51 E

V

I n e V

' x 2 = 1. (2)

Наличие в выражении (2) слагаемого 2z₂x₂r₅₁E_x2 приводит к связи z₂-, x₂- поляризован-ных волн и повороту главных осей эллипса показателей преломления в плоскости x₂z₂ на угол 0 (рис. 5). В частном случае, когда уравнение (2) симметрично относительно переменных x₂, z 2 , угол 0 постоянен и равен п /4 •

Тогда преобразование осей x₂, z₂ к новым главным осям x₃, z₃ примет вид:

Х2 = r2 cos 0 - r2 sin 0

1 r r         r ³

z 2 = x з sin 0 + z з cos 0 •

Подставляя систему выражений (3) в уравнение (2) и полагая коэффициент при x₃z₃ равным нулю, получим показатели преломления для новых осей и угол их поворота 0 :

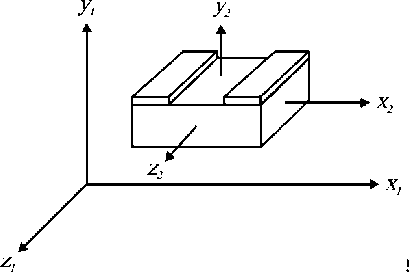
Рис. 4. Ориентация оптических осей кристалла в СКЭП

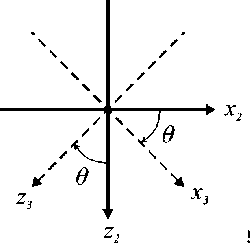
Рис. 5. Поворот главных осей эллипса показателей преломления в плоскости x₂z₂

nx 3 = cos (0) sin (0)         cos2(0) + 2r E sin(0)cos(0)

2 ⁺    2     ^r 22 Ey 2cos ^{( 0 ) +} 2r 5i Ex 2^{sin( 0 )}c^{os( 0 )}

n ₀ ²        n_e ²

ⁿz 3 =

Вывод: для реализации рассмотренного типа фазирования оптической поверхности ЭОК должен иметь как минимум 2 ненулевых элемента матрицы электрооптических коэффициентов, обуславливающих влияние ортогональных составляющих электрического поля на показатель преломления и фазовую функцию волн промежуточных поляризаций.

Данный способ управления оптическим элементом может быть реализован для большего числа материалов по сравнению с предыдущим методом, однако также не позволяет использовать наиболее эффективные кристаллы классов 2mm, 4mm.

ВЛИЯНИЕ ОРИЕНТАЦИИ ОСЕЙ

ЭЛЕКТРООПТИЧЕСКОГО КРИСТАЛЛА.

СЛУЧАЙ, КОГДА ОДНА ИЗ ОСЕЙ

ЭЛЕКТРООПТИЧЕСКОГО КРИСТАЛЛА ПАРАЛЛЕЛЬНА БАЗИСНОМУ ВЕКТОРУ СКЭП И НАПРАВЛЕНИЮ

РАСПРОСТРАНЕНИЯ

СВЕТОВОЙ ВОЛНЫ

Рассмотрим частный случай ориентации ЭОК, когда одна из его оптических осей (например, ось анизотропии z₂ ) сонаправлена с осью СКЭП (например, z₁ ) и направлением распространения световой волны, а две другие ориентированы под произвольным углом а к базисным векторам x₁,y₁ СКЭП (рис. 6).

Переход от системы координат x₁ , y₁ СКЭП к x₂ , y₂ СКК будет осуществляться с помощью матрицы A линейного преобразования [4]:

хэ     x

² = A ¹

V y 2 J    V y 1 J

f " 11 a 2 Jf x i J

V a 21 a 22 ^JV y 1 J

Если оси x₂, y₂ ортогональны и угол между векторами x 1 , x 2 составляет а , то элементы a_j; матрицы в выражении (5) равны a 11 =cos( а ), a₁₂ =sin( а ), a₂₁ =-sin( а ), a₂₂ =cos( а ):

jr 2 = x 1 cos( а ) + y 1 sin( а )

У 2 = - x 1 sin ( а ) + У 1 cos( а ) ^.

Таблица 2. Требования к матрице электрооптических коэффициентов

Направление светов ой волны	Составляющие электрического поля в СКК	Электрооптические коэффициенты	Класс симметрии кристалла
z 2 ||y 1	Ez 2 , Ex 2	r11, r63 r13, r61 r11, r13, r61 r11, r13, r63 r11, r61, r63 r13, r61, r63 r11, r13, r61, r63	1 1,3,3m 1,3 1 1 1 1
	Ez 2 , Ey 2	r22, r63 r23, r62 r22, r23 ,r62 r22, r23, r63 r22, r62, r63 r23, r62, r63 r22, r23, r62, r63	1,2 1 1 1,3 1 1 1
y 2 ||y 1	Ey 2 , Ex 2	r11, r52 r12, r51 r11, r12, r51 r11, r12, r52 r11, r51, r52 r12, r51, r52 r11, r12, r51, r52	1,3,32 1,3,3m 1,3 1,3 1,3 1,3 1,3
	Ey 2 , Ez 2	r32, r53 r33, r52 r32, r33, r52 r32, r33, r53 r32, r52, r53 r33, r52, r53 r32, r33, r52, r53	1,m 1,2 1,3,4,6 1 1 1 1
x 2 ||y 1	Ex 2 , Ey 2	r21, r42 r22, r41 r21, r22, r41 r21, r22, r42 r21, r41, r42 r22, r41, r42 r21, r22, r41, r42	1,m,3,3m 1,2,3 1,3 1,3 1,3 1,3 1,3
	Ex2, Ez2	r31, r43 r33, r41 r31, r33, r41 r31, r33, r43 r31, r41, r43 r33, r41, r43 r31, r33, r41, r43	1,m 1,2,3,4,6 1 1 1 1 1

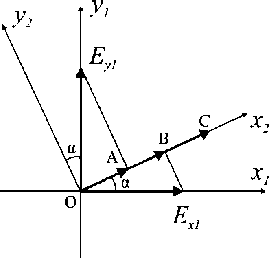
Рис. 6. Ориентация осей x₂ , y₂ кристалла относительно базиса x₁ , y₁ СКЭП

Переход из системы СКК в СКЭП будет осуществляться аналогичным образом с помощью обратной матрицы A-1, равной:

a - 1=[ A11 a 211 [ A ] l A12 A22 J где [A] – определитель матрицы A (в данном случае равный 1). Элементы A11, A12, A21, A22 являются алгебраическими дополнениями a11, a12, a21, a22 и соответственно равны cos(a ), -sin(a ), sin(a ), cos(a ):

x 1 = ^r 2 cos( a ) - y 2 sin ( a ) y = x₂ sin( a ) + y 2 cos( a ) ^.

Таким образом, между базисами СКК и СКЭП существует однозначная связь, определяемая углом поворота a , позволяющая по заданным координатам элемента (вектора, точки, плоскости) в одной системе координат определить его положение в другой системе.

Используя рассмотренный выше математический аппарат, определим электрические поля E_x2, E_y2 , наведенные составляющими E_x1, E_y1 и действующие вдоль оптических осей кристалла x₂, y₂ .

В дальнейшем будем учитывать только абсолютные значения векторов поля, поскольку их направления при расчете величины электрооптического эффекта не принципиальны.

Исходя из сделанных утверждений, для величин E_x2, E_y2 с учетом выражения (6) можно записать:

b ₁₁ x ₂ ²

+ 2 b

12 ^x 2 ^y 2

⁺ b 22 ^y 2

= 1.

Для приведения квадратичной формы (9) к каноническому виду Bx 2 + Cy 2 необходимо вместо переменных x₂, y₂ подставить их значения, выраженные через новые оси x₃, y₃ :

x 2 = x g cos( 0 ) - y з sin( 0 ) y 2 = x g sin ( 0 ) + y g cos( 0 ) .

где 0 - угол поворота новых осей относительно осей СКК. Тогда выражение (9) примет вид:

x _g ² [ b 11 cos² ( 0 ) + 2 b ₁₂ sin( 0 ) cos( 0 ) + b ₂₂ sin² ( 0 ) ] +

+ y 2 [ b _H sin² ( 0 ) - 2 b ₁₂ sin( 0 ) cos( 0 ) + b ₂₂ cos² ( 0 ) ] +

+ x _g y _g [ - 2 b ₁₁sin( 0 )cos( 0 ) + 2 b ₁₂(cos 2 ( 0 ) -        . (11)

- sin² ( 0 )) + 2 b ₂₂ sin( 0 ) cos( 0 ) ] = 1

E_x 2 = Ex 1 cos( a ) + Ey 1 sin( a )

Для приведения (11) к канонической форме приравняем множитель при x₃y₃ к нулю:

Ey 2 =

- Ex i sin ( a ) + Eyi cos( a )

- 2 b 11 sin( 0 )cos( 0 ) + 2 b ₁₂ (cos²( 0 ) -

- sin² ( 0 )) + 2 b ₂₂ sin( 0 )cos( 0 ) = 0

Необходимо отметить, что в общем случае E 2 +E_{y2 <}  E x1 +E_y1 вследствие того, что производится векторное сложение полей, при этом ни одна из составляющих поля не может быть отрицательной.

Вид эллипса показателей преломления в плоскости x₂y₂ запишем, полагая координату z₂ =0:

Учитывая тождества

2sin( 0 )cos( 0 )=sin(2 0 )

и cos2(u)-sin2(0 )=cos(20 ), разделим (12) на cos(20 ) и выразим из него пе ременную 0:

0 = 2 arctg

^{2 b} 12

к bn ^- b 22

⁺ r ^{11 2}

к X 2

^{+ r}12 ^Ey 2

^x 2 +

+

' 1

"T ⁺ r 21 Ex 2

\

^{+ r}22 ^Ey 2 ^y 2

+

к ny 2

^{+ 2 x} 2 ^y 2 ^{( r} 61 ^Ex 2 ^{+ r} 62 ^Ey 2

. 7

)= 1

. (8)

где составляющие E_x2, E_y2 определены в (7).

Последующий анализ электрооптического эффекта по выражениям (7), (8) включает в себя две задачи:

• 1)    определение новых главных осей x₃, y₃ эллипса показателей преломления в системе СКК при наличии внешних электрических полей и положения новых осей в СКЭП с помощью матрицы перехода A^-1;

• 2)    определение показателя преломления n_y4 для волны с произвольным вектором поляризации y₄ и положения (координат) этого вектора в СКЭП.

С целью упрощения анализа перепишем (8) в виде:

Из (13) следует, что при одинаковых значениях b 11 , b .2 угол 0 будет равен п /4 , при b₁₂ =0 значение 0 будет равно 0 при любых b 11 , b₂₂ , т.к. в отсутствие электрического поля деформации индикатрисы не происходит. Коэффициенты b₁₁, b₁₂, b₂₂ в общем случае содержат не только показатели преломления материала, но также электрооптические константы и величины действующих электрических полей, поэтому угол поворота оптических осей для b₁₁, b₂₂ будет зависеть от напряженности поля.

Поскольку при задании системы (10) полагалось, что поворот осей x₂, y₂ происходит в положительном направлении против хода часовой стрелки, то для нахождения положения осей x₃, y₃ в СКЭП (векторы x_3,1 , y_3,1 ) справедливы зависимости:

x g 1 = x 1 cos( a + 0 ) + y g sin( a + 0 )

y g,1 =- x g sin ( a + 0 ) + y g cos( a + 0 )

r g 1 E x 1 tg ( a + 0 )

y g,1 =- x 1 ctg ( a + 0 )

Для определения показателя преломления n_p для световой волны произвольной поляризации

p₂ воспользуемся квадратичной формой (9). Состояние поляризации зададим в виде вектора, ориентированного под углом в к оси х 2 :

Р 2 = P x 2 ^Х2 + P y 2 y 2 = ^X2 cos C # ^{) +} y 2 sin ^(в ) .(14)

Как следует из (14), вектор поляризации p лежит на прямой y₂ = tg( в )x (аналогично рис. 5).

Для нахождения показателя преломления в точке (x_2,1;y_2,1), (-x_2,1;-y_2,1) решим систему уравнений:

^b11 x 2 ⁺ b 22 y 2 ^{+ 2} x 2 y 2 ^b 12 = ¹

. У 2 = tg ^(в ) x 2

Значение показателя преломления n_p определится как модуль вектора, соединяющего центр координат x₂, y₂ и найденное решение, например (x_2,1;y_2,1). Решая систему (15) стандартным методом подстановки и учитывая тригонометрическое тождество 1 + tg²( в ) = 1/cos 2 ( в ) , найдем значение n_p :

n p = V x 2,1 ⁺ y 2,1 =

=---------- ,           ¹                      . (16)

cos ( в )V b„ + 2 b„ tg ( в ) + b 22 tg ² ( в )

Для упрощенного определения положения вектора p₂ в исходной системе координат x₁, y₁ , без использования матриц линейного преобразования, можно воспользоваться зависимостью:

P\ = P x 1 x ⁺ P y 1 ^y1 = ^x 1 co^{s ( a + в ) +}

+ У 1 sin ( a + в )

^P 1 ^c У 1 = tg ^{( a + в} ) ^x 1

. (17)

где знак “+” перед a , в соответствует углам, откладываемым в положительном направлении, знак “-” - для углов a , в , откладываемых в от- рицательных направлениях.

В случае, когда вектор поляризации задается в системе СКЭП в виде p₁=x₁cos( y )+y^in( y ) , а затем преобразуется в СКК с целью нахождения показателя преломления, для определения вектора p₂ в базисе x₂y₂ предлагается воспользоваться формулой:

^P 2 = P x 2 r 2 ⁺ P y 2 ^y 2 = ^x 2 ^{cos (}Y ^{- a ) +}