Особенности физически-нелинейного расчета железобетонных балок-стенок с трещинами при знакопеременном нагружении

Для знакопеременного нагружения принципиальную важность имеет решение вопроса об учете накопления остаточных деформаций в бетоне при изменении знака напряжений. Принятый в данной работе подход показан на примере трансформации условной диаграммы деформирования бетона при одноосном напряженном состоянии (рис. 1).

До смены знака напряжений в бетоне остаточные деформации определяются как сумма нелинейных деформаций, вызванных напряжениями текущего знака, и деформаций усадки (точка Вi-1). Со сменой знака напряжений на диаграмме осуществляется перенос вершины секущей с углом наклона α через начало координат (точка Вi). В результате меняется знак не только упругих, но и остаточных деформаций, чем обеспечивается соответствие физическому смыслу задачи при алгоритмизации расчета. Таким образом, смена знака деформаций позволяет сохранить параметры физического состояния бетона после изменения нагрузки – уровень напряжений, момент трещинообразования и др. Подробная методика учета накопления остаточ- ных деформаций при плоском напряженном состоянии рассмотрена в работе [2].

Для расчета по предложенной методике была выбрана балка-стенка W-4 специальной конструкции, предназначенная для испытаний на малоцикловую нагрузку и исследованная в опытах К. Герстле и В. Червенки [4]. В балке-стенке длиной 1830 мм и толщиной 76,2 мм предусмотрены три поперечных ребра сечением 298 × 102 мм, обеспечивающих реверсивный характер приложения нагрузки. Армирование конструкции - одной сеткой из стержневой арматуры периодического профиля ∅ 7,6 мм и шагом 76,2 мм (коэффициенты армирования µ х = µ у = 0,00785). Физико-механические свойства арматуры приведены в табл. 1.

Таблица 1

Арматура	E , МПа s ,	σ s,el , МПа	σ 0,2 , МПа	σ u , МПа	ε su
∅ 7,6 мм	1,9 × 105	290	353	550	0,02*

* Принято по аналогии со стержневой арматурой с подобными показателями прочности.

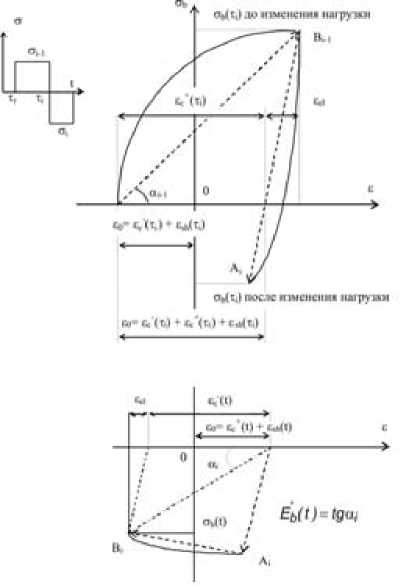
Рис. 1. Условная диаграмма деформирования бетона при знакопеременном нагружении

Физико-механические свойства бетона балки-стенки приведены в табл. 2.

Таблица 2

Физико-механические свойства бетона балки-стенки

Цилиндрическая прочность Rс, МПа	Кубико-вая прочность R (20 x 20 см), МПа	Призменная прочность Rb*, МПа	Прочность при осевом растяжении Rbt, МПа	Модуль мгн.-упр. деформаций Еb, МПа
24,45	29,45	21,6**	1,97**	20000

* Вычислено по формуле R b = R c /0,83;

** Вычислены как средние значения при коэффициенте вариации 13 %.

Секущие модули деформаций бетона определялись по методике диаграмм-изохрон, подробно изложенной в работе [1]. Для эталонной диаграммы-изохроны было принято s _b ( т ) = 2,5 х х 10 - . В качестве меры линейной ползучести была использована функция, рекомендованная в работе [3], параметры которой составили С 0 = =7 х 10 5 B i = 0,75; _{Г 1} = 0,008; В₂ = 0,2; у ₂ = 0,01.

Схема армирования балки-стенки W-4, совмещенная со схемой загружения, приведена на рис. 2. Для расчета часть балки-стенки, примыкающая к продольному ребру, была разбита на 110 прямоугольных конечных элементов двух типов: толщиной 298 мм для опорного ребра (элементы № 1, 12, …, 100) и 76,2 мм для остальных. Число узлов в системе составило 138.

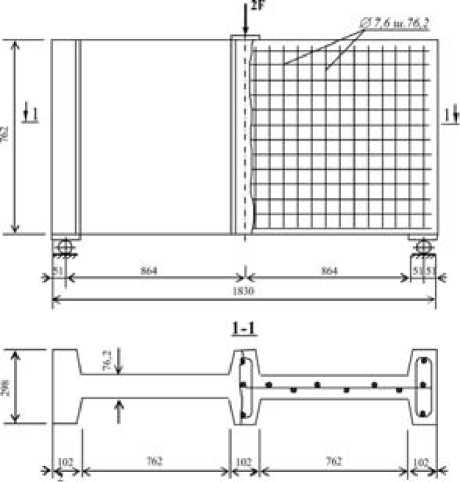
Рис. 2. Схема армирования балки-стенки W-4 [3]

Каждый полуцикл нагружения балки-стенки был разделен на 20 ступеней, F max = 7,3 + 19 х 5 = =102,3 кН. Время выдержки нагрузки на каждой ступени нагружения было принято 3 мин. Таким образом, для расчета балки-стенки использовались диаграммы-изохроны жесткого режима за-гружения с параметрами t — т от 3 мин до t — т = 3 х 100 = 300 мин.

На рис. 3 представлены графики прогиба балки-стенки на 2½ цикла нагружения.

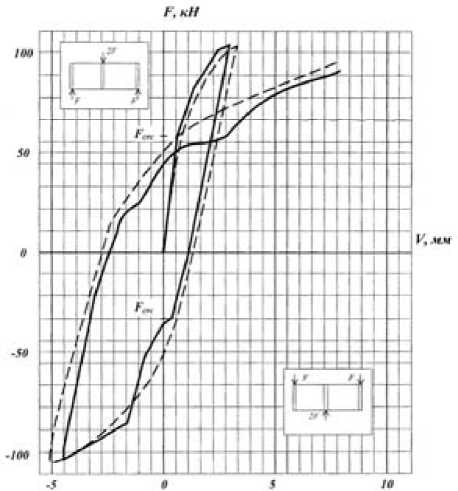
Рис. 3. Кривая прогиба балки-стенки W-4 при циклическом нагружении из опытов [4]

Примечание. _________ опыт; ______ расчет.

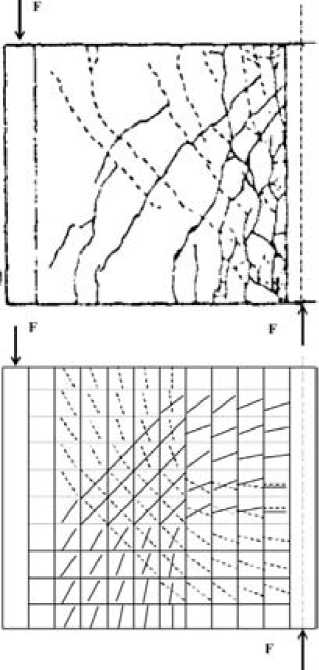
Рис. 4. Схема образования и раскрытия трещин в балке-стенке W-4 [1].

Примечание. Вверху – опыт, внизу – расчет. Пунктир – схема трещин на ½ цикла, сплошная линия – на 1½ цикла.

На первом полуцикле нагружения расчетная нагрузка трещинообразования составила 58 кН, что практически совпало с опытом. Дальнейший рост нагрузки привел к развитию характерной системы трещин (показана пунктиром на рис. 4), которые практически полностью закрылись на втором полуцикле нагружения (разгрузке). На 1½ цикла нагружения нагрузка трещинообразования составила 32,4 кН. Дальнейший рост нагрузки привел к развитию характерной системы трещин (показана сплошной линией на рис. 4). При этом нелинейность деформирования существенно возросла, а прогиб балки-стенки в конце 1½ цикла нагружения возрос практически в два раза по сравнению с прогибом на первой ½ цикла. Деформирование балки-стенки на 2 и 2½ цикла нагружения сопровождалось существенным раскрытием первичной системы трещин и резким нарастанием нелинейности деформирования. Прогиб балки-стенки в конце 2½ цикла нагружения более чем в три раза превысил прогиб на первой ½ цикла. Наряду с этим анализ напряженного состояния конечных элементов показал, что часть продольной и поперечной арматуры сетки в конце ½, 1½ и 2½ цикла нагружения работала в пластической стадии, чему соответствует значительная ширина раскрытия трещин, зафиксированная в опыте.

Сопоставление результатов расчета и опытных данных позволяет сделать вывод, что деформационная теория железобетона с трещинами с достаточной степенью точности описывает нелинейное поведение конструкций при знакопеременном малоцикловом нагружении.