Особенности фокусировки оптических вихрей при изменении высоты нечетных и четных зон рельефа субволновых элементов

Развитие микроэлектроники проводит к потребности в миниатюризации элементов, что, в свою очередь, стимулирует прогресс в технологиях литографии [1 –6]. На текущий момент классическим решением является использование ультрафиолетового света в фотолитографическом процессе [2]. Следует отметить, что в общем случае дифракция света ограничивает разрешение традиционной фотолитографии, что привело к внедрению новых методов литографии, среди которых нужно отметить электронно-лучевую литографию [2, 3], ионно-лучевую литографию [7], рентгеновскую литографию [8], двухслойную фотолитографию на основе перекрытия позитивного и негативного фоторезиста и контролируемого времени экспозиции [9]. Причем интегративные методики, основанные на сочетании позитивного и негативного фоторезиста, достаточно часто используются, в том числе для изготовления коаксиальных передатчиков [10]. Для реализации схем с разрешением менее 10 нанометров известно использование гибридных органонеорганических фоторезистов [11].

Главной особенностью сред с градиентным показателем преломления (GRIN) является неоднородность распределения показателя преломления в пространстве [12– 19], причем такие среды можно классифицировать в зависимости от формы поверхностей, у которых показатель преломления постоянен [13]. Известно выделение симметричных относительно заданной координаты сред GRIN [13] и произвольных сред GRIN (также известных как F-GRIN), где наблюдается произвольное трехмерное распределение показателя преломления [14]. Хорошо известно использование материалов с градиентным показателем преломления для управления распространением света [20, 21], коллимации света [22, 23], для решения задач оптической связи [24], в биологии [25, 26], причем для проектирования таких сред также применяются нейронное сети [16].

Последние десятилетия оптические вихри активно используются для решения ряда задач в оптике и фотонике [27–42], в частности, для оптического манипулирования [20, 27, 40–44], зондирования [45], оптической передачи информации [32, 46], острой фокусировки [20, 34, 35, 47]. Для генерации таких пучков можно использовать ряд оптических структур, среди которых можно отметить спиральные фазовые пластинки [27, 49, 50], металинзы и метаповерхности [27, 51], кольцевые решетки [52–54]. Кольцевые решетки и дифракционные аксиконы в различных комбинациях также используются для получения оптических игл с большой глубиной фокуса [55–57].

В данной работе, с целью выявления особенностей фокусировки, было проведено исследование дифракции оптических вихрей с круговой, радиальной, азимутальной поляризацией на субволновых кольцевых решетках со стандартной и GRIN-подложкой. Варьировалась высота нечетных и четных зон рельефа элементов.

Численное моделирование осуществлялось методом конечных разностей во временной области (FDTD).

1.    Дифракция оптических вихрей на обычных и GRIN-подложках

В данной работе анализируется действие трех разных типов подложек: стандартная подложка с показателем преломления n = 1,47, а также две разновидности GRIN-подложек, у которых показатель преломления изменяется равномерно от максимального значения в центре к минимальному на краях (прямая GRIN-подложка) и обратный случай, когда минимальный показатель преломления находится в центре и происходит его равномерное увеличение к краям подложки (обратная GRIN-подложка).

Максимальный показатель преломления в случае GRIN-подложек была равен 2,7, минимальный n = 1,47, шаг изменения показателя преломления равен 0,123. Следует отметить, что GRIN-подложку составляли кольца одинаковой ширины с различным радиусом, равномерно вписанные друг в друга по подложке размером 16,5Х х 16,5Х х Х. Ширина девяти вписанных в подложку колец составляла 0,75λ (с радиусами от 1,5λ до 7,5λ), радиус центрального элемента составлял 0,75λ.

Моделирование методом FDTD осуществлялось со следующими параметрами моделирования: рассматривалась трехмерная расчетная область (8,4 мкм), со всех сторон окруженная поглощающим слоем PML (0,6 мкм). В качестве входных пучков рассматривались оптические вихри первого порядка (мода Лагерра– Гаусса (1,0), σ =1,5 мкм) с круговой, радиальной и азимутальной поляризациями.

Следует отметить, что в данной работе «-» круговой поляризацией будет называться поляризация, у которой знак круговой поляризации противоположен знаку введенной вихревой фазовой сингулярности. Обратный случай будет называться «+» круговой поляризацией.

Длина волны λ входного излучения была равна 0,532 мкм. Шаг моделирования по пространству – λ /30, шаг по времени – λ /(60c), где c – скорость света. Для численного моделирования использовался программный пакет Meep [58].

В качестве элементов в работе были рассмотрены дифракционные аксиконы и кольцевые решетки. Период рассматриваемых оптических элементов был одинаков и составлял 1,05λ. Высота рельефа h элементов выбиралась исходя из скачка фазы π радиан. Для выбранного показателя преломления рельефа элемента ( n =1,47) базовая высота h составляла 1,06 λ (π). В дальнейшем варьировалась высота нечетных ( h 1 ) и четных ( h 2 ) зон рельефа элементов, также исходя из скачка фазы π радиан.

На рис. 1 показано прохождение рассматриваемого оптического вихря через стандартную подложку и GRIN-подложки при «-» круговой поляризации входного пучка. Также на рисунке схематично показано расположение подложки и приводится вид входного пучка.

Хорошо заметно, что в случае GRIN-подложки высотой λ наблюдается фокусировка излучения. Таким об- разом, добавление рельефа к такой подложке очевидно приведет к лучшей фокусировке.

А в случае обратной GRIN-подложки хорошо видно рассеивание входного излучения и можно предположить, что при таком рельефе будет наблюдаться удлинение светового отрезка при сравнении с обычной подложкой.

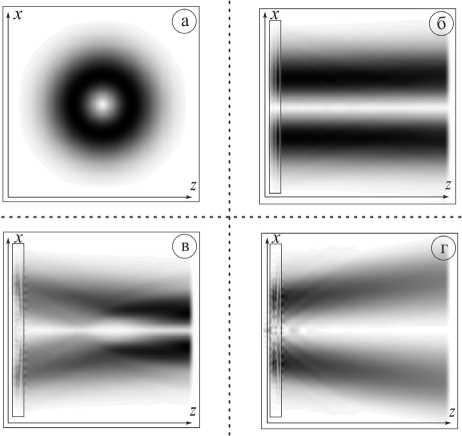
Рис. 1. Входной пучок (а) и его распространение через стандартную подложку (б), прямую GRIN-подложку (в) и обратную GRIN-подложку (г), интенсивность

Ранее было показано, что возможно распознавание поляризации дифракционным аксиконом для оптического вихря первого порядка для стандартной подложки, в том числе кремниевой [29, 59].

Тогда близкие к нулевым значения центрального фокального пятна должны указывать на «+» круговую и радиальную поляризации, а ненулевое значение указывает на «–» круговую и азимутальную поляризации. Оценим влияние на распознавание поляризаций GRIN-подложек.

Следует отметить, что размер фокального пятна оценивался по стандартной ширине полуспада максимального значения интенсивности (full width at half maximum – FWHM) в точке максимальной интенсивности на оптической оси, аналогично была проведена оценка длины световой иглы вдоль оси распространения излучения (depth of focus – DOF).

На рис. 2 показано распространение оптического вихря через дифракционный аксикон с высотой рельефа h =1,06λ при круговой, радиальной и азимутальной поляризациях.

Поперечные картины дифракции в максимумах интенсивности вне элемента для стандартной подложки приведены на рис. 3. В остальных случаях поперечные картины дифракции выглядят схожим образом.

Как видно из рис. 2, возможно распознавание всех рассмотренных типов поляризации, причем азимутальную поляризацию можно отличить от «-» круговой поляризации по меньшему размеру фокального пятна.

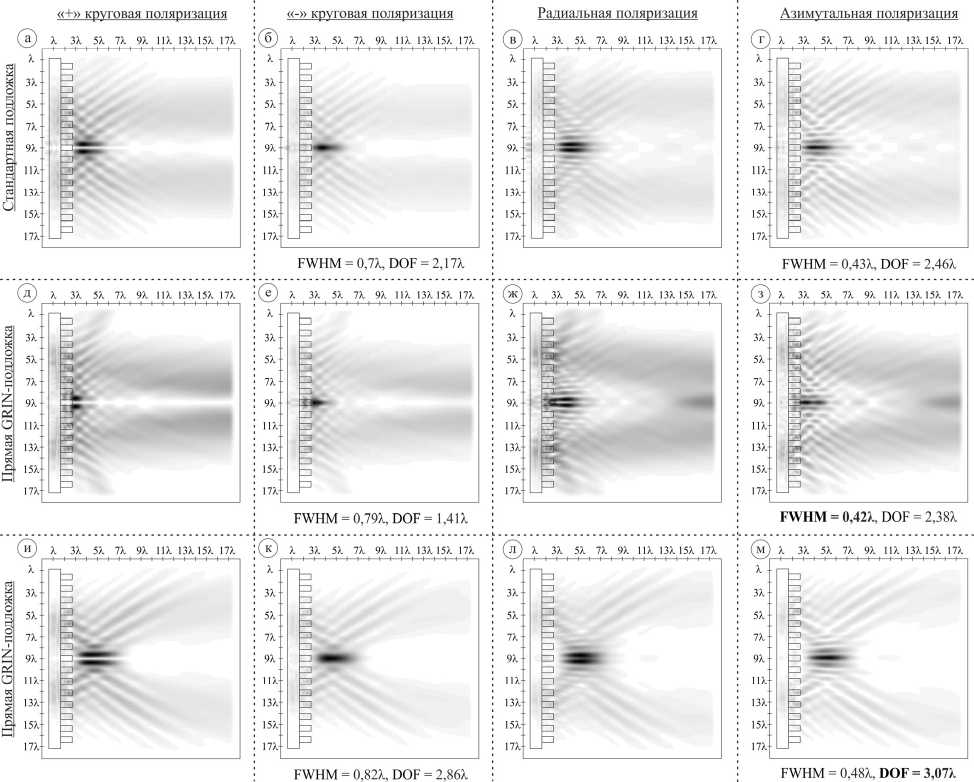
Рис. 2. Дифракция оптических вихрей (плоскость xz, высота рельефа аксикона h = 1,06λ) при различных типах поляризации и стандартной подложке (а, б, в, г), прямой GRIN-подложке (д, е, ж, з) и обратной GRIN-подложке (и, к, л, м)

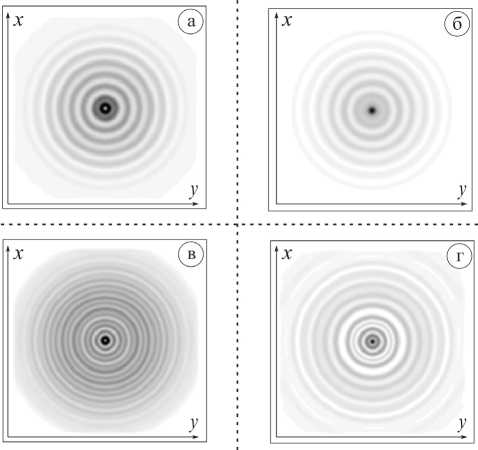
Рис. 3. Двумерная картина дифракции (плоскость xy) в максимумах интенсивности (стандартная подложка, рис. 2) при различных типах поляризации: «+» круговой (а), «-» круговой (б), радиальной (в), азимутальной (г)

А радиальную поляризацию от «+» круговой поляризации можно отличить по более резкому падению интенсивности формируемого кольца, а также меньшему размеру центрального тёмного пятна.

Влияние обратной GRIN-подложки проявляется в возможности определения типа поляризации на более далеком расстоянии от элемента путем формирования более длинной световой иглы (DOF=3,07λ, азимутальная поляризация).

Влияние прямой GRIN-подложки проявляется в формировании в общем случае более узких и коротких фокальных отрезков. Именно с помощью данного типа подложки было получено наиболее узкое фокальное пятно (FWHM=0,42λ) для случая азимутальной поляризации.

Также следует отметить, что для данного типа подложки при радиальной поляризации вдали от элемента наблюдается увеличение значения интенсивности на оптической оси.

Оценим, как изменение высоты рельефа элементов c GRIN-подложкой влияет на дифракцию рассматриваемых оптических вихрей.

В дальнейших исследованиях будем рассматривать «-» круговую, радиальную и азимутальные поляризации входного лазерного излучения. Размер подложки будет аналогичен подложкам, рассмотренным в данном параграфе (высотой λ).

• 2.    Фокусировка оптических вихрей при изменении высоты нечетных и четных зон рельефа для прямой GRIN-подложки

Ранее было показано, что изменение высоты рельефа существенным образом меняет картину дифракции в ближней зоне субволновых оптических элементов [20, 34, 39]. Рассмотрим элементы, у которых варьируется высота нечетных и четных зон рельефа. Подобный оптический элемент фактически представляет собой комбинацию двух аксиконов, даю- щих два фокуса на разном привести к формированию расстоянии, что может нескольких пиков ин-

тенсивности на оптической оси. Оценим, как увеличение высоты рельефа элемента будет влиять на фокусировку лазерного излучения.

Будем рассматривать два типа элементов. В первом случае зафиксируем высоту рельефа h 1 = 1,06λ и будем варьировать h 2 кратно скачку фазы π радиан: 2,13λ (2π), 3,19λ (3π), 4,26λ (4π), 5,32λ (5π). Во втором случае, наоборот, фиксируем h 2 = 1,06λ и аналогичным образом изменяем h 1 .

Полученные результаты для элемента первого типа для прямой GRIN-подложки показаны на рис. 4 (плоскость xz ), для элемента второго типа приведены на рис. 5. Значения DOF и FWHM приведены в максимумах на оптической оси вне элемента. Как и ранее, на рисунках в плоскости xz схематично показан профиль рассматриваемого элемента, а также местоположение максимумов на оптической оси (для случаев, когда их несколько).

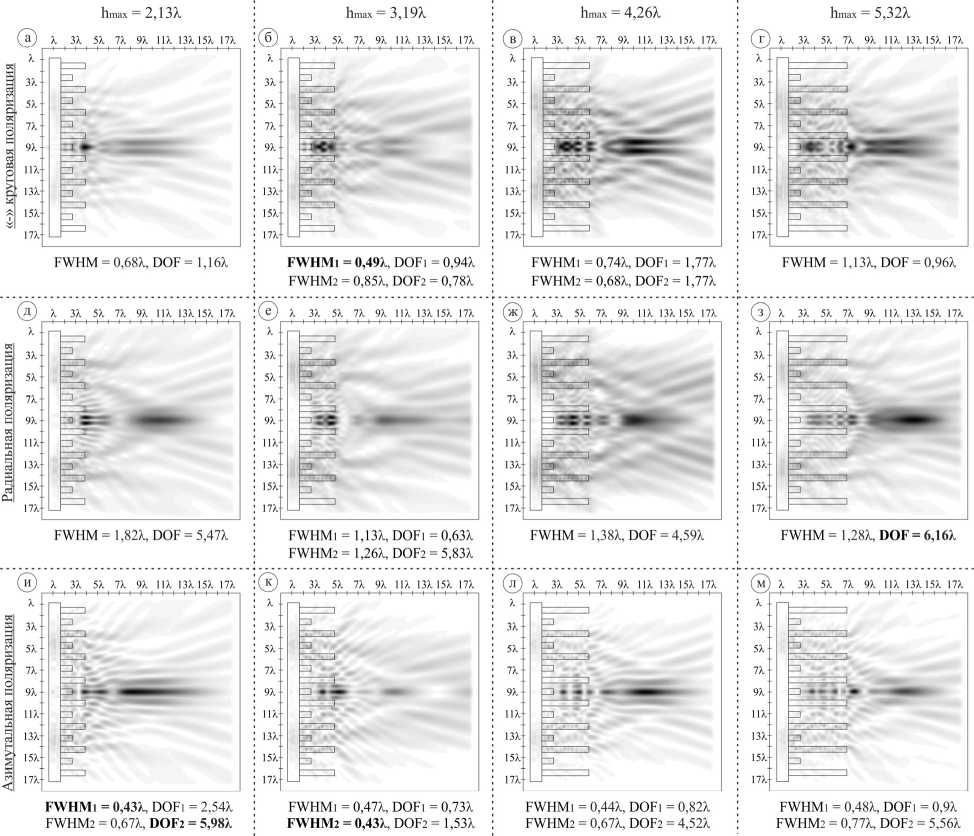
Рис. 4. Двумерная картина дифракции (плоскость xz) оптических вихрей на кольцевых решетках (общая интенсивность, прямая GRIN-подложка) при фиксированном h 1 = 1,06λ и h 2 = 2,13λ, 3,19λ, 4,26λ, 5,32λ: (а, б, в, г) «-» круговая поляризация, (д, е, ж, з) радиальная поляризация, (и, к, л, м) азимутальная поляризация

Оценим случай, когда h1 = 1,06λ и изменяется высота h2. В этом случае все основные максимумы фор- мируются вне элемента. Увеличение высоты h2 привело к формированию мощной световой иглы для ра- диальной поляризации, в отличие от случая той же поляризации для обычного аксикона с высотой h1 = 1,06λ (наблюдался минимум на оптической оси и формирование кольца). Максимальный размер световой иглы для радиальной поляризации DOF=6,16λ.

Минимальный размер фокального пятна был получен для азимутальной поляризации при h 2 = 3,19λ (FWHM=0,43λ), во втором максимуме на оптической оси. Также следует отметить, что для азимутальной поляризации увеличение высоты привело к формированию набора максимумов на оптической оси. Также наблюдается формирование длинной световой иглы, причем для случая h 2 = 2,13λ (DOF = 5,98λ).

Для «–» круговой поляризации увеличение высоты h 2 больше 2,13λ привело к формированию набора оптических ловушек.

Проанализируем далее случай, когда фиксируется h 2 и варьируется h 1 (рис. 5).

Минимальный размер фокального пятна был получен рядом с рельефом элемента для «-» круговой поляризации (FWHM=0,4λ), что лучше фокального пятна, полученного для аксикона с прямой GRIN-подложкой при одинаковой высоте всех зон высоте h = 1,06λ и азимутальной поляризации.

Дальнейшее увеличение рельефа приводит к формированию основных максимумов внутри рельефа или, в случае h 1 = 5,32λ, к уширению фокального пятна. Для высоты рельефа h 1 наблюдаются одиночные оптические ловушки, но они менее выражены, чем для предыдущего типа рельефа.

Максимальный размер световой иглы был получен для радиальной поляризации при h 1 = 5,32λ, DOF=7,86λ, что в 2,56 раза длиннее лучшего случая для дифракционного аксикона при одинаковой высоте всех зон (рис. 2 м ).

Для азимутальной поляризации наблюдаются длинные световые иглы при h 1 = 2,13λ (2π, DOF =4,23λ) и h 1 =4,26λ (4π, DOF= 5,7λ), при уменьшении их длины для случаев h 1 = 3,19λ и h 1 = 5,32λ.

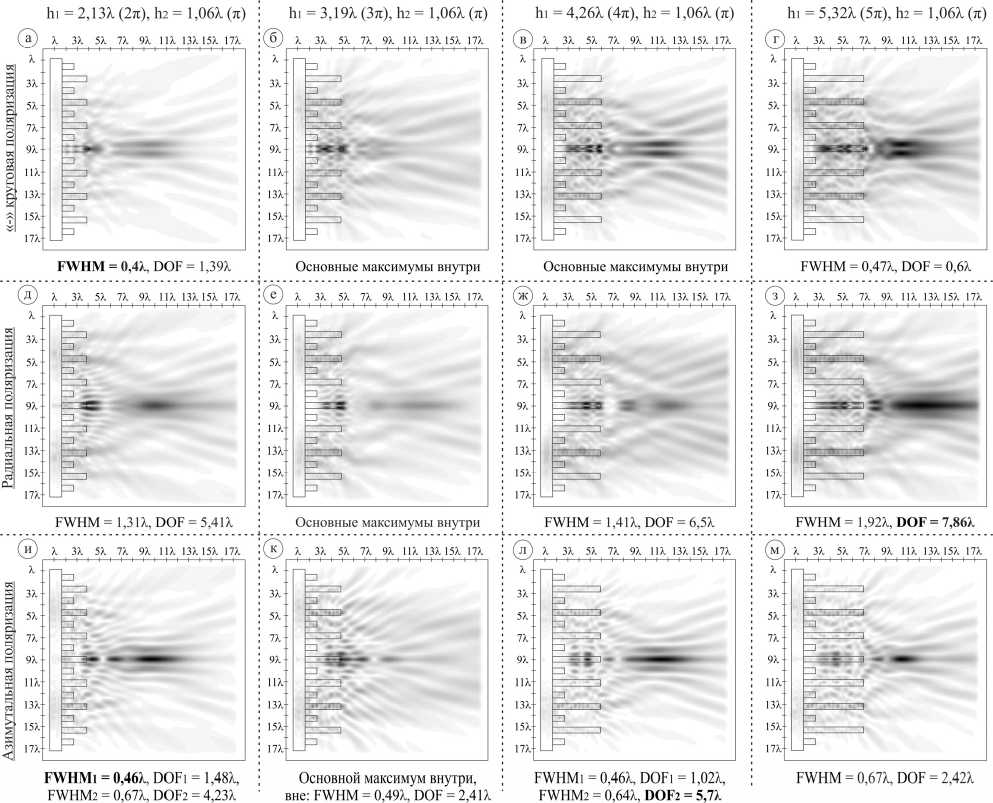
Рис. 5. Двумерная картина дифракции (плоскость xz) оптических вихрей на кольцевых решетках (общая интенсивность, прямая GRIN-подложка) при h 1 = 2,13λ, 3,19λ, 4,26λ, 5,32λ и фиксированном h 2 = 1,06λ: (а, б, в, г) «-» круговая поляризация, (д, е, ж, з) радиальная поляризация, (и, к, л, м) азимутальная поляризация

• 3.    Фокусировка оптических вихрей при изменении высоты нечетных и четных зон рельефа для обратной GRIN-подложки

В данном параграфе приводятся аналогичные исследования по влиянию на картину дифракции в ближней зоне изменения высоты нечетных и четных зон рельефа, но уже при обратной GRIN-подложке. Также сначала фиксируется h 1 и меняется h 2 (рис. 6).

Размер фокальных пятен ожидаемо шире, тем не менее, для азимутальной поляризации при h 1 = 1,06λ и h 2 = 2,13λ, размер фокального пятна (FWHM =0,46λ) в первом максимуме сопоставим с аналогичным видом рельефа при прямой GRIN-подложке (FWHM=0,43λ, рис. 4 и ). Увеличение высоты рельефа также приводит к формированию набора максимумов интенсивности на оптической оси для данного типа поляризации.

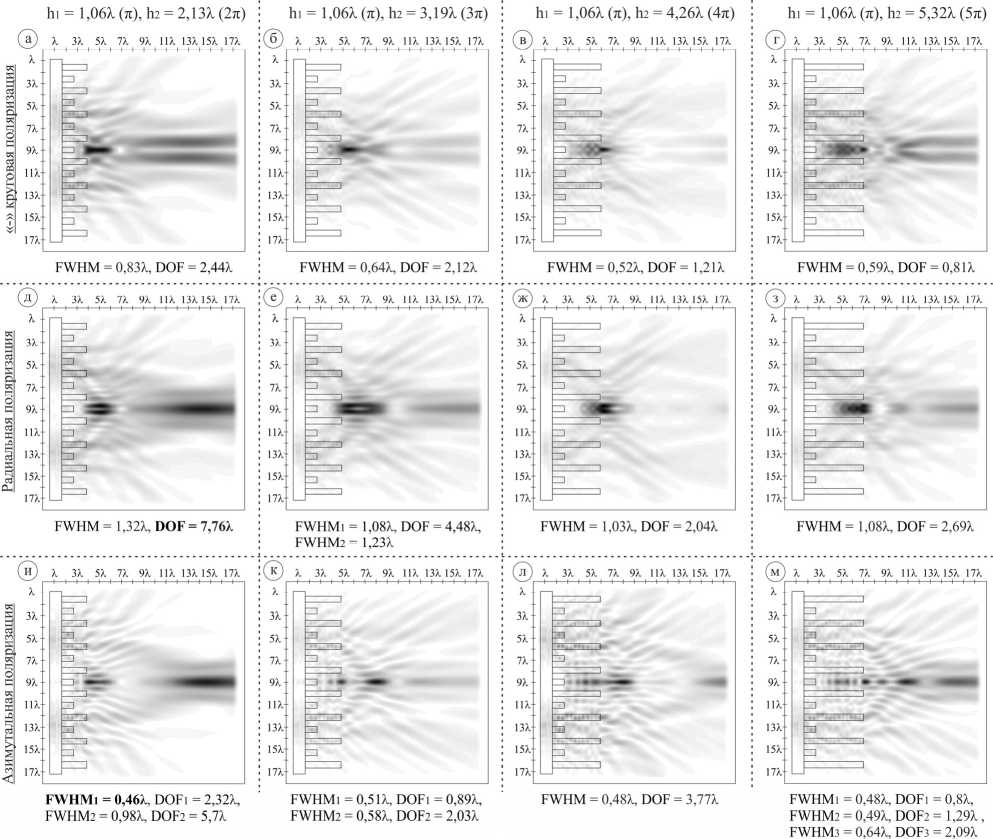
Рис. 6. Двумерная картина дифракции (плоскость xz) оптических вихрей на кольцевых решетках (общая интенсивность, обратная GRIN-подложка) при фиксированном h 1 = 1,06λ и h 2 = 2,13λ, 3,19λ, 4,26λ, 5,32λ: (а, б, в, г) «-» круговая поляризация, (д, е, ж, з) радиальная поляризация, (и, к, л, м) азимутальная поляризация

Максимальный размер световой иглы был получен для радиальной поляризации, случай h 1 = 1,06λ и h 2 = 2,13λ (DOF = 7,76λ), что сопоставимо с размерами световой иглы для прямой GRIN-подложки (DOF=7,86λ), однако при меньшей высоте рельефа.

Также следует отметить, что для радиальной поляризации при h 1 = 1,06λ и h 2 = 3,19λ (рис. 6 е ) наблюдается формирование «оптической бутылки», области пониженной интенсивности, окруженной со всех сторон максимумами интенсивности [43, 60].

Сечения в плоскости xy и график интенсивности в плоскости xz для этого случая представлены на рис. 7. Высота максимумов интенсивности (точки 1 и 3 на рис. 7) оптической ловушки в плоскости xz составляет 75,6% и 77,5% от максимальной интенсивности. Длина области пониженной интенсивности L=1,21λ.

При анализе сечения в области минимума (точка 2 рис. 7) следует отметить образование кольца, максимум которого в данной точке составляет 89,1% от максимальной интенсивности. В этом случае ширина теневого фокального пятна определяется как FWHM=0,27λ, в то время как ширина кольца составляет FWHM=0,36λ. Также следует отметить, что одиночная оптическая ловушка наблюдается для того же типа поляризации при h2 = 3,19λ.

Далее зафиксируем h 2 и будем варьировать h 1 (рис. 8).

В этом случае максимальный размер световой иглы наблюдается для радиальной поляризации при h 1 = 2,13λ и h 2 = 1,06λ (DOF = 8,04λ), что в 2,62 раза длиннее лучшего случая для дифракционного акси-кона при одинаковой высоте всех зон (DOF=3,07λ).

Минимальный размер фокального пятна (FWHM=0,41λ) получен для «-» круговой поляризации при h 1 = 4,26λ и h 2 = 1,06λ, что сопоставимо с лучшим ранее полученным случаем для прямой GRIN-подложки (FWHM=0,4λ) также для «-» круговой поляризации.

Таким образом, предложенные в данной работе элементы с чередующимися шагами, которые представляют собой комбинацию двух аксиконов, дополненные GRIN-подложками, позволяют сформировать требуемую картину дифракции в ближней зоне: узкое фокальное пятно, оптическую иглу, оптические ловушки. При сравнении результатов данной работы с ранее проведенными исследованиями по изменению высоты рельефа [20, 34, 39, 42] следует отметить, что удалось добиться увеличения размеров светового фокального отрезка: световая игла, полученная в данной работе, на 32,4% длиннее ранее полученной световой иглы, DOF=6,07λ [20].

Также следует отметить, что для дифракционного аксикона применение обратной GRIN-подложки позволяет расширить возможности распознавания поляризации лазерного излучения, показанные ранее [29, 59]: возможно определить состояние поляризации на более далеком расстоянии от рельефа элемента.

Заключение

В данной работе методом FDTD было проведено моделирование дифракции оптических вихрей первого порядка с круговой, радиальной, азимутальной поляризацией на субволновых кольцевых решетках со стандартной и GRIN-подложкой. Варьировалась высота нечетных и четных зон рельефа элементов, таким образом, элементы представляли собой комбинацию двух дифракционных аксиконов.

Показано, что можно подобрать поляризацию лазерного излучения и параметры элемента таким образом, чтобы на оптической оси формировалась длинная оптическая игла, узкое фокальное пятно, одиночные оптические ловушки и их наборы.

Минимальное фокальное пятно было получено для «-» круговой поляризации (FWHM=0,4λ) при h 1 = 2,13λ, h 2 = 1,06λ и прямой GRIN-подложке.

Максимальная световая игла на оптической оси была получена для элемента с чередующимися зонами ( h 1 = 2,13λ, h 2 = 1,06λ) для обратной GRIN-подложки при радиальной поляризации лазерного излучения, DOF = 8,04λ.

Также показано, что обратную GRIN-подложку целесообразно использовать при распознавании поляризации лазерного излучения вследствие формирования более длинного светового отрезка, чем для стандартной подложки при аналогичном типе рельефа элемента.

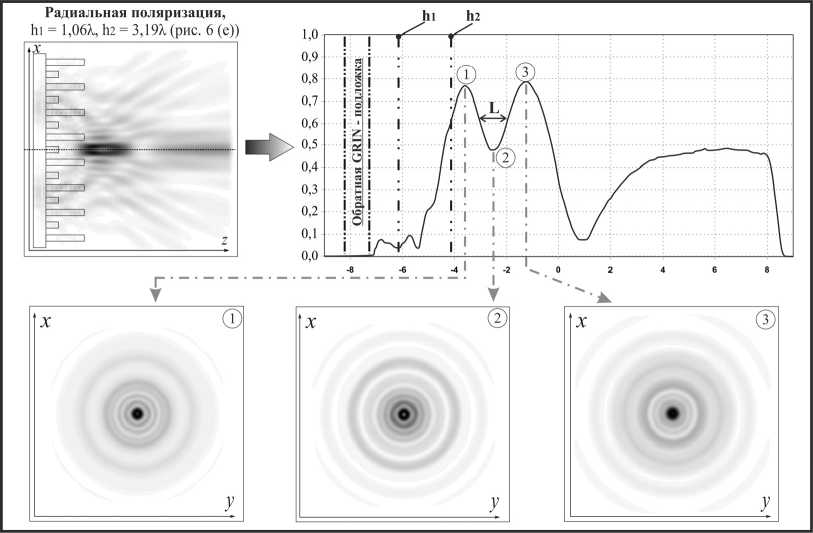
Рис. 7. Формирование оптической ловушки при радиальной поляризации и высоте рельефа h 1 = 1,06λ, h 2 = 3,19λ

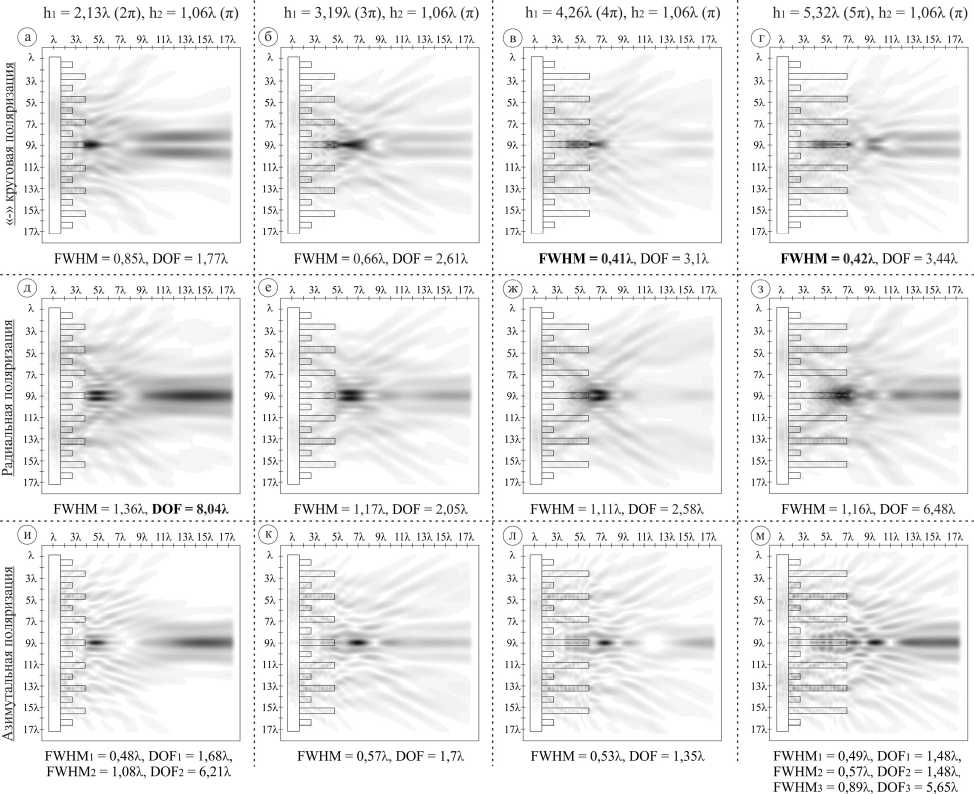
Рис. 8. Двумерная картина дифракции (плоскость xz) оптических вихрей на кольцевых решетках (общая интенсивность, обратная GRIN-подложка) при h1 = 2,13λ, 3,19λ, 4,26λ, 5,32λ и фиксированном h2 = 1,06λ: (а, б, в, г) «-» круговая поляризация, (д, е, ж, з) радиальная поляризация, (и, к, л, м) азимутальная поляризация

Исследование выполнено за счет гранта Российского научного фонда № 24-22-00044,