Особенности фокусировки поверхностных акустических волн на сфере

нако такие модели работают только в пространствах нулевой кривизны. Поэтому, например, при объяснении эффекта отклонения светового пучка в гравитационных полях используют как модель эффективной неоднородной среды, так и модель пространств конечной кривизны геометрии Н.И. Лобачевского. Пространства конечной кривизны для моделей волнового распространения могут естественным образом возникать и на малых, по сравнению с космическими, масштабах, если исследуются поверхностные волны, распространяющиеся по ( n – 1)-мерным границам n -мерных объектов, погруженных в n -мерное пространство.

В данной работе рассматриваются особенности распространения поверхностных волн Релея на сфере [1–3] как простой пример пространства конечной кривизны. Геометрическое описание процесса распространения таких волн сводится к анализу лучевых семейств и их особенностей,

ВЕСТНИК 2014. ВЫПУСК 4

ВЕСТНИК 2014. ВЫПУСК 4

отражающих не только «классические» волновые эффекты: дифракцию, интерференцию, фокусировку, – но и специфические эффекты, обусловленные «собственной кривизной» среды распространения.

Использование геометрических моделей дает простой инструмент для анализа многочисленных возможностей в изменении конфигурации источников поверхностных волн, зон неоднородностей, отклонений поверхности от идеальной формы и др. В частности, относительно просто проводить оптимизацию датчиков, работающих на эффекте распространения поверхностных акустических волн.

2. Лучевые семейства поверхностных акустических волн на сфере

Поле поверхностной волны (волны Релея), излучаемой криволинейным источником S на однородной сфере, может быть представлено в следующей интегральной форме:

U (M_v t_ep ) =

= U o Re

^eXP⁽ - ikV R t ep ) j

L t -

exp( ik^R 6 ⁽ t )) dl J sin ^ ( t )

, (1)

где источник представляет собой кривую линию на сфере, заданную параметрически:

⁶ ( t ) , t G [ t H , t k ],                (2)

| ф 0 ⁽ t )

точка наблюдения Q определена координатами ( 6 1 , 9 1 ) на поверхности сферы (рис. 1). Здесь мы использовали интегральное представление для релеевской волны из [4], полученное для источника в виде отрезка дуги большого круга, модифицировав его для случая источника в виде произвольной кривой. U ₀ – амплитудный множитель, заданный мощностью излучателя, V_R – фазовая скорость, k = 2 π/λ – волновое число поверхностной волны, t_вр – временная компонента и R – радиус сферы. Угол θ – центральный угол между элементом линейного источника S и точкой наблюдения Q( 6 ₁, 9 ₁), который из геометрии задачи задается как:

6 ( t ) = arccos(cos 6 0 ( t ) cos 6 1 cos( ^ 1 - ф ₀ ( t )) +

+ sin 6 ₀( t )sin 6 1 ).              (3)

Обозначения углов в (1), (2) соответствуют рис. 1. Интегрирование в (1) ведется вдоль излучающей линии, начало и конец которой заданы угловыми координатами ( θ_н , φ_н ) и ( θ_к , φ_к ). Источник расположен так, что пересекает точку (п/2,0) на сфере, а отсчет 6 ₀( t ) производится от значения π/2.

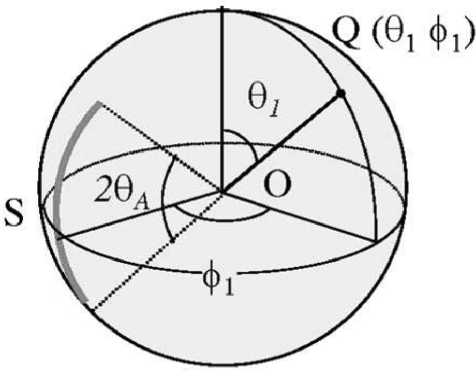
Рис. 1. Сфера и источник S на сфере

Элемент длины источника dl можно найти из соотношения:

dl = arccos(cos 6 ₀ cos( 6 ₀ + 6 ₀ dt ) cos( ^ ₀ + ф ₀dt - 9 ₀) + + sin 6 ₀ sin( 6 ₀ + 6 ₀ dt )) ,

поэтому dl = (60)2 + (90)2cos2 60 dt.        (4)

В итоге формула (1) примет вид:

^{U (} 9 1 , Ф 1 , t ep ) = U 0 ^{Re ex}P^{( -} ikV R t ep ) ^

→

t r exp( ikR 6 (t ))     T2    ^    2

'У ,, + ^ ₀ cos ^ ⁽ t ) dt

. - t H

д/ sin ^ ( t )

. (5)

Основной вклад в значение интеграла (5) при kR >> 1 дают следующие особые точки (см., например, [5–7]):

• а)    стационарные точки фазовой функции осциллирующего ядра, для которых

• 6 .

  - 6 ( t ) = 0 ,                (6)

о t соответствуют геометрооптическим лучам на сфере;

• б)    концевые точки интеграла t_к и t_н , порождающие краевые лучи на сфере;

• в)    полюса, связанные с особенностями амплитуды поля элементарного источника в антиподных точках, где sinθ ( t ) = 0, т.е. θ = 0, θ = π .

• 3.    Моделирование лучевых структур и волнового поля «линейного» источника на поверхности сферы

Анализ геометрии этих особых точек позволяет относительно просто интерпретировать расчетные картины распределения поля релеев-ских волн, которые могут быть получены вычислением по формуле (5).

Рассмотрим распространение поверхностных акустических волн (ПАВ), излучаемых источником, представляющим собой отрезок дуги большого круга. Условно его будем называть «линейным».

В свободном пространстве излучение линейного источника интерпретируется лучевой картиной, состоящей из семейства геометрооптических лучей, исходящих ортогонально источнику, и двух семейств краевых лучей, радиально расходящихся от концевых точек. Однако на сфере геометрооптические лучи представляют собой не параллельные прямые (в плоскости источника), а большие круги на сфере, которые имеют общую точку на угловом расстоянии θ = π /2 (рис. 2). Таким образом, геометрооптические лучи, «параллельные» в окрестности источника, фокусируются на указанном расстоянии в соответствии с моделью Н.И. Лобачевского. Фокусировка данного типа обусловлена исключительно кривизной пространства, в котором распространяется волна, потому мы назовем такой тип фокусировки фокусировкой Лобачевского.

Концевые точки источника, генерирующие краевые лучи, определяют два лучевых семейства, которые в окрестности концевых точек имеют радиально расходящуюся структуру, но далее также формируют фокальные точки указанного типа в антиподах на расстоянии θ = π.

Поскольку дифракционные лучи иллюстрируют дифракционную расходимость излучения, источником которого является источник конечной апертуры, то для поверхности сферы,

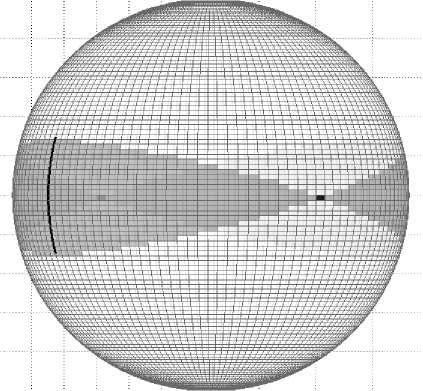
Рис. 2. Лучевая картина от линейного источника на сфере

Рис. 3. Распределение энергии поля от линейного источника на сфере при kR = 400

вследствие эффекта фокусировки Лобачевского, можно компенсировать фокусировкой дифракционную расходимость, выбрав оптимальные размеры источника в зависимости от длины волны (см. [4; 8–10]).

Иллюстрацией лучевого описания распространения ПАВ, излучаемой «линейным» источником, служат рис. 2 и 3. На рис. 2 представлена лучевая картина, а на рис. 3 – структура волнового поля, определенная по формуле (5).

На рис. 2 в белой зоне присутствуют только два краевых луча, а геометрооптических лучей нет, в серой зоне – 1 геометрооптический луч и два краевых, в черной зоне – бесконечное число геометрооптических лучей (число лучей равно числу рассматриваемых элементов источника) и два краевых луча. В антиподе, при θ = π, формируется точная копия лучевой структуры, которая имеет место в окрестности заданного источника.

Распределение энергии поля полностью согласуется с представлениями о фокусировке и интерференции рассмотренных лучевых семейств рис. 2. Результаты расчетов поля совпадают с результатами, полученными в [8] именно для такого вида источников.

• 4.    Моделирование лучевых структур и волнового поля «криволинейного» источника на поверхности сферы

В случае, если источником поверхностных волн является линия переменной кривизны, на сфере возникают зоны фокусировки и дивергенции лучей, которые конкурируют с фокусировкой Лобачевского и дифракционной расходимостью. В итоге, как геометрическая структура лучевых семейств, так и суммарное волновое поле достаточно сложны для анализа. По этой причине вопросы оптимизации распределения поля ПАВ по

ВЕСТНИК 2014. ВЫПУСК 4

поверхности сферы эффективнее решаются с использованием геометрических лучевых моделей.

В качестве простейшего криволинейного источника ПАВ на сфере рассмотрим симметричный отрезок параболы. Геометрия лучевой картины представлена на рис. 4.

На рис. 4 в белой зоне присутствуют два краевых дифракционных луча, источниками которых являются концевые точки источника; в светлосерой зоне – только 1 геометрооптический луч и два краевых; в черной зоне (в центре) – 3 геометрооптических луча, организующих фокальную

ВЕСТНИК 2014. ВЫПУСК 4

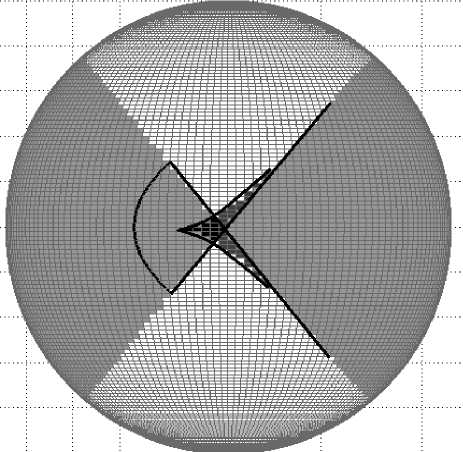
Рис. 4. Лучевая картина от параболического источника на сфере

структуру типа А3 с ограничениями, обусловленными конечной апертурой источника, и два краевых; в темно-серой (симметрично снизу и сверху от оси симметрии рисунка) – 2 геометрооптических и два краевых, причем в точках сопряжения граничных геометрооптических лучей и каустических ветвей особенностей А2 образуются особенности В3; на границе светло-серой и белой зон имеем особенность В2 (классификация указанных особенностей рассмотрена, например в [5–7]).

Лучевая картина и соответствующее распределение амплитуды волнового поля (рис. 5) аналогичны излучающей параболе на плоскости. Так же наблюдается особенность типа А3 – «каустическое острие» и усиление поля на краевых особенностях: взаимодействие каустик типа А2 и краевых лучей. Но, в отличие от плоского случая, на сфере наблюдается повторная симметричная фокусировка типа А3 в антиподе (геометрия этой особенности на рис. 4 не показана) и «повторная» фокусировка Лобачевского для дифракционных лучей в антиподных точках по отношению к краевым точкам источника.

5.    Применение эффектов фокусировки и автоколлимации ПАВ на сфере

Особенности фокусировки ПАВ на сферической поверхности позволяют сформировать автоколлимированный (нерасходящийся) волновой пучок, способный многократно огибать сферу. Оценка размера линейного источника, обеспечивающего данное свойство, дается формулой [4; 9]:

Рис. 5. Распределение амплитуд (слева) и энергии (справа) поля от параболического источника на сфере при kR = 200

Эта формула, в частности, показывает, что оптимальный угловой размер источника равен углу коллимации и уменьшается с увеличением волнового параметра kR . Другими словами, более тонкий коллимированный пучок формируется при большем значении kR .

Принцип действия шарового ПАВ-датчика следующий [4]. На экваторе непьезоэлектрического шара с тонкой пьезоэлектрической пленкой или же пьезоэлектрического монокристаллического шара размещена чувствительная пленка, на которую направляется коллимированный пучок. Генерация и детектирование волны после одного, двух и так далее проходов происходит с помощью встречно-штыревого преобразователя (ВШП). Скорость и ослабление ПАВ изменяются вследствие поглощения молекул детектируемого вещества чувствительной пленкой. Хотя для небольших концентраций такое изменение очень мало, из-за многократных (до 50 раз) проходов оно значительным образом усиливается. Это и позволяет детектировать небольшое линейное ослабление ПАВ.

Учитывая, что с помощью источника переменной кривизны можно создать также и зону фокусировки ПАВ в контролируемой области сферы, то, подбирая геометрию излучателя и геометрию и параметры чувствительной пленки, можно еще улучшить характеристики ПАВ-датчика.

Заключение

Таким образом, проведенное моделирование показывает эффективность применения методов геометрической оптики геометрической теории дифракции и для анализа особенностей распространения и фокусировки поверхностных волн. Данный подход обобщается на случаи ПАВ, распространяющихся на объектах эллипсоидальной формы, конической и цилиндрической форм, для задач распространения ПАВ на искривленных неоднородных поверхностях, а также на поверхностях, имеющих дефекты, являющиеся резкими (в масштабах длины волны) границами для релеевских волн (например, разломы и трещины).