Особенности фокусировки супер-гауссовых пучков с круговой и радиальной поляризациями на кольцевых решетках с переменной высотой колец рельефа
Автор: Савельев Дмитрий Андреевич
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 4 т.46, 2022 года.
Бесплатный доступ
В данной работе проведено исследование особенностей фокусировки супер-Гауссова пучка, а также мод Лагерра-супер-Гаусса (1,0) с радиальной и круговой поляризациями на кольцевых решетках с переменной высотой колец рельефа. Рассматривалось изменение высоты рельефа от максимальной высоты в центре до минимальной на краях элемента (прямая кольцевая решетка) и обратный случай, когда максимум высоты рельефа был на краях и минимум в центре (обратная кольцевая решетка). Сравнение осуществлялось с действием дифракционного аксикона с сопоставимым периодом решетки. Численное моделирование осуществлялось методом конечных разностей во временной области. Было показано, что изменение высоты колец рельефа элементов существенным образом влияет на дифракционную картину в ближней зоне. В частности, для супер-Гауссова пучка использование прямой кольцевой решетки позволило уменьшить размер фокального пятна на 18,7 % для радиальной поляризации (σ = 5 мкм), использование обратной кольцевой решетки привело к уменьшению фокального пятна на 36,9 % (σ = 12,25 мкм) по сравнению с действием дифракционного аксикона. Также в работе было показано, что при освещении обратной кольцевой решетки модой Лагерра-супер-Гаусса (1,0) с круговой поляризацией наблюдается формирование узкой и протяженной области пониженной интенсивности на оптической оси (оптической ловушки).
Кольцевые решетки, супер-гауссов пучок, моды лагерра-супер-гаусса (1, 0), острая фокусировка, дифракционный аксикон, оптическая ловушка
Короткий адрес: https://sciup.org/140295008
IDR: 140295008 | DOI: 10.18287/2412-6179-CO-1131
Текст научной статьи Особенности фокусировки супер-гауссовых пучков с круговой и радиальной поляризациями на кольцевых решетках с переменной высотой колец рельефа
Гауссовы пучки и вихревые пучки известны своим использованием для решения многих задач в оптике [1–8], в том числе для увеличения пропускной способности систем связи [9, 10] и для передачи информации по оптоволокну [11]. Для однородной поляризации (линейной и круговой) лазерного излучения фазовая сингулярность используется для усиления продольной компоненты электрического поля в области фокуса [4, 12, 13], что может использоваться для ряда приложений, среди которых можно отметить оптическое манипулирование и обработку материалов [2, 14]. Цилиндрически поляризованные пучки [2, 15– 18] также привлекают все большее внимание исследователей [19–21], в том числе благодаря связи между фазовой сингулярностью (в скалярном поле) и поляризационными особенностями (в векторных по- лях) [22], а также характерному для радиальной поляризации сильному продольному электрическому полю в фокальной области [12, 23–33].
Для формирования протяженного светового отрезка вдоль оптической оси достаточно часто используются аксиконы [34–38], в том числе их дифракционные аналоги (кольцевые решетки) [39, 40]. Изменение высоты рельефа оптического элемента существенным образом влияет на картину дифракции лазерного излучения [36, 39–42]. В частности, изменение высоты дифракционного аксикона от 0,25λ до 3λ (рассматривались супер-Гауссовые пучки) привело как к острой фокусировке (с размером фокального пятна, взятого по ширине полуспада интенсивности, вплоть до четверти длины волны), так и к формированию протяженного светового отрезка вплоть до трех длин волн [40].
В данной работе проведено исследование особенностей фокусировки супер-Гауссовых пучков с круговой и радиальной поляризациями на кольцевых решетках с переменной высотой отдельных колец рельефа. Также было проведено сравнение таких решеток с дифракционным аксиконом. Численное моделирование (3D) осуществлялось методом конечных разностей во временной области (FDTD) [43], реализованном в свободно распространяемом программном продукте Meep [44].
1. Исследование дифракции супер-Гауссова пучка на кольцевых решетках переменной высоты
В данном параграфе исследуется дифракция суперГауссова пучка на кольцевых решетках переменной высоты. Супер-Гауссовые пучки используются в тех случаях, когда требуется равномерное распределение интенсивности по сечению пучка [40, 45, 46]. Такие лазерные пучки также характеризуются более резким спадом интенсивности на краях пучка.
Параметры моделирования: длина волны X = 0,532 мкм, общий размер вычислительной области вместе с поглощающим слоем, со всех сторон окружающим вычислительную ячейку: 13,5Х х 13,5Х х 13,5Х. При этом размер вычислительной ячейки x , y , z е [5,6 X ; 5,6 X ], а толщина поглощающего слоя PML~ 1,15 X . Шаг выборки по пространству - X /30, шаг по времени - X / (60c), где c - скорость света. Показатель преломления материала рассматриваемых элементов n = 1,5.
В качестве входного лазерного излучения рассматривался супер-Гауссов пучок с радиальной и круговой поляризацией (знак круговой поляризации противоположен знаку внесенной вихревой фазовой сингулярности, см. параграф 2).
При таком типе круговой поляризации, как было показано ранее [13, 39], наблюдается перераспределение энергии между компонентами электромагнитного поля, выраженное в усилении продольной компоненты электрического поля на оптической оси.
Амплитуда супер-Гауссова пучка определяется выражением [40]:
A ( r ) = exp
rp
2 g p
где σ – это размер пучка в мкм, степень p =6.
На рис. 1 приведены примеры входных пучков.
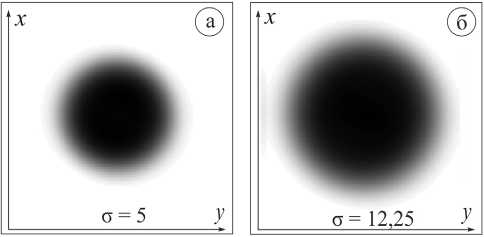
Рис. 1. Входные пучки, общая интенсивность, суперГауссов пучок: (а) σ = 5 мкм, (б) σ = 12,25 мкм
Результаты исследований для рассматриваемых оптических элементов приведены на рис. 2 (круговая поляризация) и рис. 3 (радиальная поляризация).
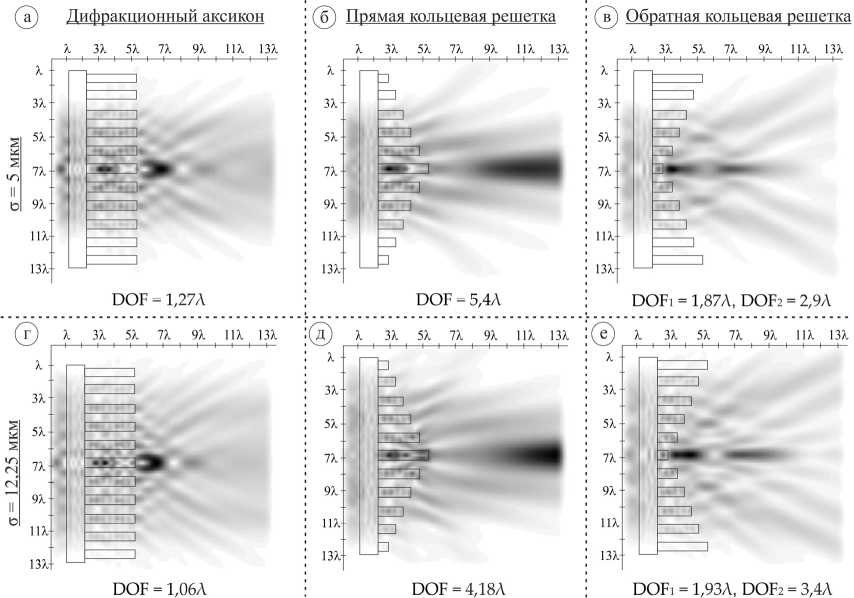
Рис. 2. Двумерная картина дифракции супер-Гауссова пучка с круговой поляризацией на кольцевых решетках переменной высоты в плоскости x z, общая интенсивность (размер области - 13,5Х х 13,5Х)
DOF = 1,97A
DOF = 0,96Л
DOFi = l,87A, DOFz = 3,47A
Рис. 3. Двумерная картина дифракции супер-Гауссова пучка с радиальной поляризацией на кольцевых решетках переменной высоты в плоскости x z, общая интенсивность (размер области - 13,5Х х 13,5Х)
Высота рельефа кольцевых решеток h варьировалась следующим образом: в центре h =3λ, затем высота уменьшается с каждым последующим кольцом решетки с шагом 0,5λ, до края элемента с высотой h = 0,5λ (прямая кольцевая решетка). Рассматривается и обратный случай: в центре находится минимум при h = 0,5λ, а высота далее увеличивается с аналогичным шагом вплоть до h =3λ, от центра к краю решетки (обратная кольцевая решетка). Для сравнения также рассматривался дифракционный аксикон ( h =3λ) с числовой апертурой (NA), равной 0,95. Также следует отметить, что высота рельефа бинарного элемента, соответствующая фазе π радиан при выбранном показателе преломления ( n = 1,5), равна λ. Период всех рассмотренных кольцевых решеток составлял 1,05λ.
На рис. 2 и 3, а также далее в работе размер фокального пятна на оптической оси оценивался по ширине полуспада максимального значения интенсивности (full width at half maximum – FWHM), как и длина светового отрезка (depth of focus – DOF).
Для прямой кольцевой решетки для пучка с σ =5 мкм как в случае круговой, так и в случае радиальной поляризаций основной максимум формируется внутри элемента. Тем не менее для круговой поляризации наблюдается формирование второго максимума на расстоянии больше 5λ от рельефа элемента (DOF=5,4λ). При увеличении размера пучка при круговой поляризации основной максимум формируется вне элемента, на расстоянии ~7λ от края (DOF=4,18λ). Следует отметить, что фактические значения DOF ограничены размером вычислительной области и действием поглощающего слоя PML: при большем размере вычислительной области размер DOF был бы больше.
Для обратной кольцевой решетки наблюдаются осцилляции интенсивности на оптической оси как для круговой, так и для радиальной поляризаций. Наблюдается падение интенсивности на оптической оси, и для формируемых световых отрезков лазерного пучка с σ = 12,25 мкм приведены значения DOF как ближайшего (DOF 1 ), так и последующего (DOF 2 ).
Следует отметить схожесть формируемых картин дифракции для рассмотренных типов поляризации для обратной кольцевой решетки, также стоит отметить сдвиг максимума интенсивности от края рельефа в случае радиальной поляризации по сравнению с круговой поляризацией.
Для супер-Гаусса с σ =5 мкм наблюдается увеличение длины светового отрезка при смене круговой поляризации на радиальную. Для лазерного пучка с σ = 12,25 мкм DOF 1 больше у круговой поляризации, а DOF 2 больше у радиальной поляризации. Если говорить о световом отрезке с максимальной интенсивностью, то максимальное значение было получено для случая σ =5 мкм при радиальной поляризации (DOF 1 = 2,04λ). В этом случае первый максимум (62% от максимальной интенсивности на оптической оси) формируется на расстоянии 0,48λ от рельефа, первый минимум (52% от максимальной интенсивности) – на расстоянии 0,86λ от рельефа, а глобальный максимум
(100% интенсивности) формируется на расстоянии 1,54λ от рельефа.
Далее рассмотрим поперечные картины дифракции супер-Гауссова пучка (плоскость x y ) для всех типов исследуемых кольцевых решеток в плоскости максимальной (вне элемента) интенсивности. Результаты приведены на рис. 4 (для круговой поляризации) и рис. 5 (для радиальной поляризации).
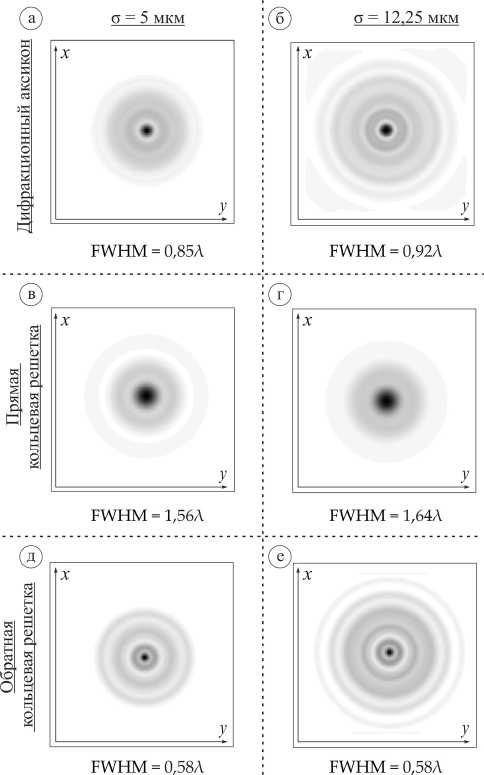
Рис. 4. Двумерная картина дифракции супер-Гауссова пучка с круговой поляризацией на кольцевых решетках переменной высоты в плоскости x y, общая интенсивность (размер области - 13,5Х х 13,5Х)
Следует отметить, что для круговой поляризации наименьшее фокальное пятно было получено для случая обратной кольцевой решетки (FWHM=0,58λ), что лучше действия дифракционного аксикона на 31,7 % для лазерного пучка с σ = 5 мкм и на 36,9 % лучше для пучка с σ = 12,25 мкм соответственно.
Для прямой кольцевой решетки в случае круговой поляризации лазерного излучения первые максимумы формируются внутри элемента, однако на расстоянии в несколько длин волн от рельефа начинает формироваться широкий и длинный фокальный отрезок. Максимум для супер-Гауссова пучка с σ =5 мкм вне рельефа элемента (83 % от максимальной интенсивности)
формируется на расстоянии 5,85λ от элемента, а для более широкого пучка (σ = 12,25 мкм) – на расстоянии 7,1λ (100 % интенсивности).
Для случая радиальной поляризации наблюдается обратная ситуация: больший размер фокального пятна был получен для обратной кольцевой решетки.
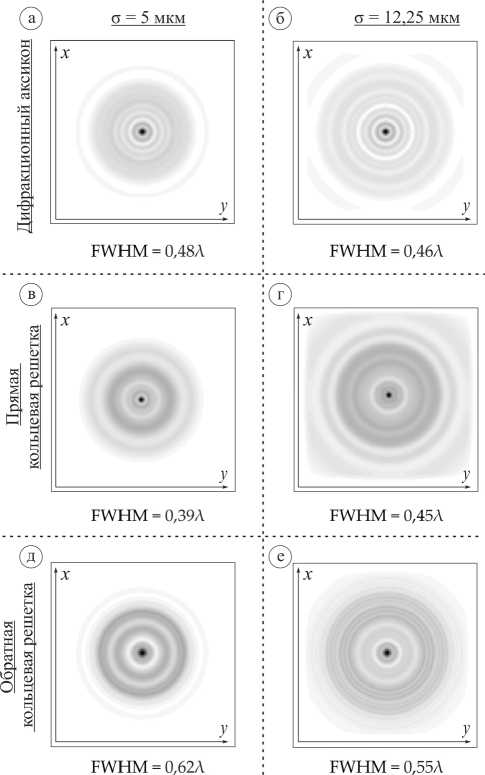
Рис. 5. Двумерная картина дифракции супер-Гауссова пучка с радиальной поляризацией на кольцевых решетках переменной высоты в плоскости x y, общая интенсивность (размер области - 13,5Х х 13,5Х)
И рис. 5 видно, что минимальный размер фокального пятна из рассмотренных случаев для радиальной поляризации супер-Гауссова пучка был получен для случая прямой кольцевой решетки при σ =5 мкм: FWHM = 0,39λ, что на 18,7 % лучше, чем действие дифракционного аксикона. Для более широкого лазерного пучка (σ = 12,25 мкм) размер фокального пятна сопоставим с размером фокального пятна дифракционного аксикона.
-
2. Исследование дифракции мод Лагерра-супер-Гаусса (1,0) на кольцевых решетках переменной высоты
Изменим входной лазерный пучок, оставив все остальные параметры моделирования теми же.
В данном параграфе приведены исследования для мод Лагерра–супер-Гаусса (1,0) также при круговой и радиальной поляризациях.
Амплитуда моды Лагерра–супер-Гаусса (1,0) определяется выражением [40]:
A ( r, ф ) = r ■ exp
rp
2 g p
■ e i » ,
где σ – это размер пучка в мкм, степень p =6.
На рис. 6 приведены примеры входных пучков.
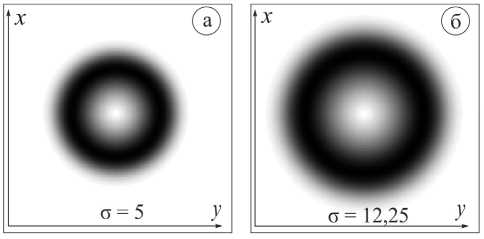
Рис. 6. Входные пучки, общая интенсивность, мода Лагерра– супер-Гаусса (1,0): (а) σ = 5 мкм, (б) σ = 12,25 мкм
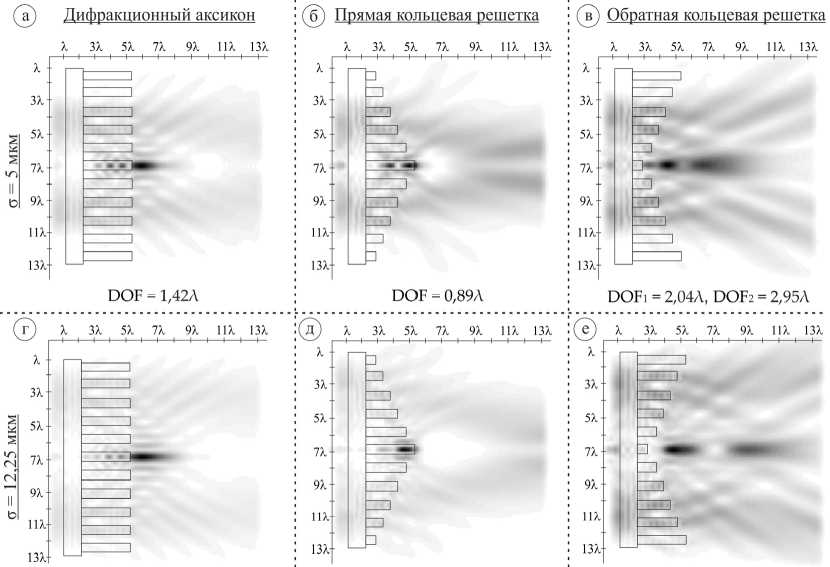
Результаты исследований для рассматриваемых кольцевых решеток в плоскости xz приведены на рис. 7 (круговая поляризация) и рис. 8 (радиальная поляризация).
Для прямой кольцевой решетки при круговой поляризации формирование максимумов наблюдается внутри элемента, за его пределами интенсивность на оптической оси падает. Оценка светового отрезка по DOF бралась в основном внутри кольцевой решетки.
Также следует отметить, что на расстоянии 4λ от рельефа и далее элемента наблюдается формирование боковых «лепестков».
Для обратной кольцевой решетки при круговой поляризации наблюдается короткий световой отрезок рядом с рельефом с последующим образованием боковых «лепестков» симметрично оптической оси. Причем для обоих случаев (σ =5 мкм и σ = 12,25 мкм) заметно пространственнонеоднородное распределение электрического поля на оптической оси и в области пространства, ее окружающего.
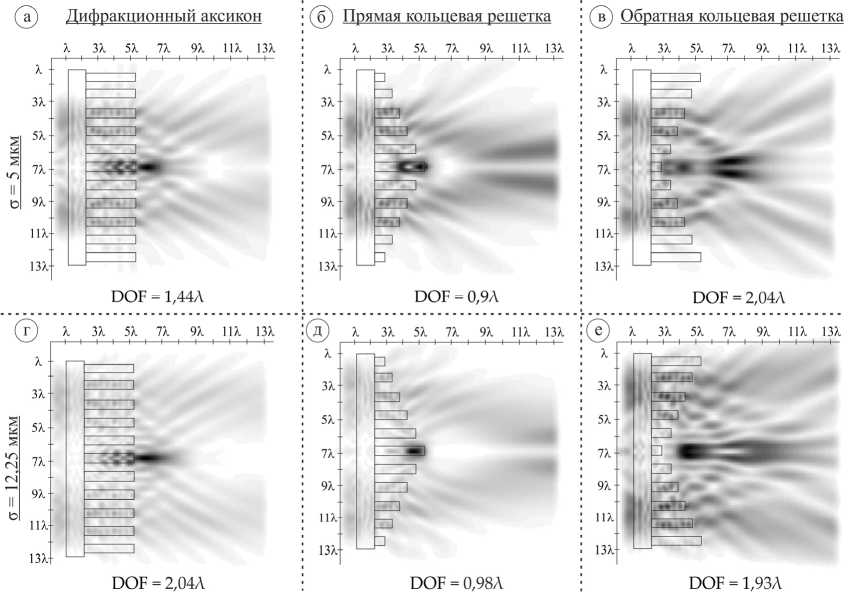
Рис. 7. Двумерная картина дифракции мод Лагерра–супер-Гаусса (1,0) с круговой поляризацией на кольцевых решетках переменной высоты в плоскости xz, общая интенсивность (размер области - 13,5Х х 13,5Х)
Особенно хорошо заметно это для случая моды Лагерра–супер-Гаусса (1,0) с σ = 12,25 мкм, где наблюдается формирование в некоторой степени оптической ловушки – «теневого» фокального отрезка, в котором интенсивность мала по сравнению с окружающими его областями пространства.
При радиальной поляризации для всех типов кольцевых решеток наблюдается первоначальное формирование боковых «лепестков», причем для случая прямой кольцевой решетки основные максимумы формируются внутри оптического элемента.
Тем не менее на расстоянии нескольких длин волн от рельефа аксикона можно видеть формирование широкого светового отрезка меньшей интенсивности на оптической оси, что особенно хорошо заметно для моды Лагерра–супер-Гаусса (1,0) с σ =5 мкм.
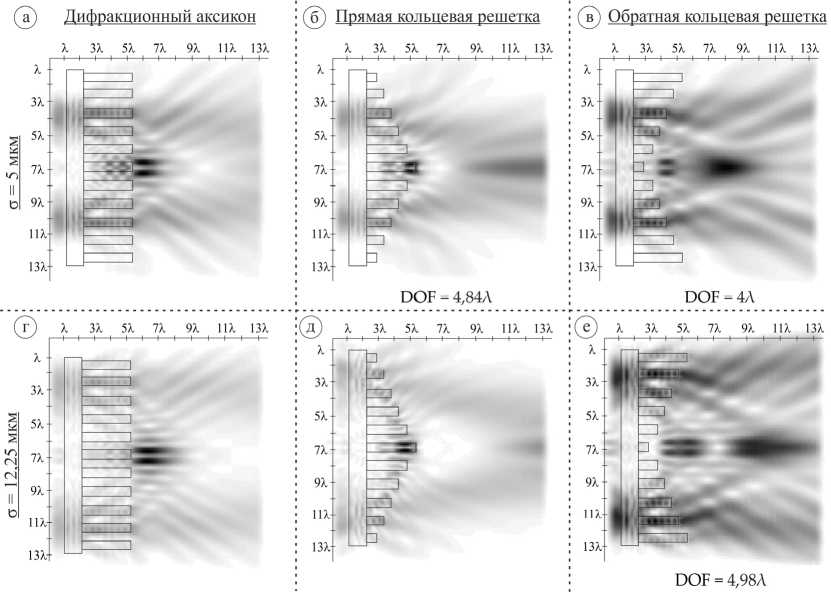
Рис. 8. Двумерная картина дифракции мод Лагерра–супер-Гаусса (1,0) с радиальной поляризацией на кольцевых решетках переменной высоты в плоскости x z, общая интенсивность (размер области - 13,5Х х 13,5Х)
Для обратной кольцевой решетки также наблюдается первоначальное формирование двух симметричных относительно оптической оси боковых световых отрезков, переходящих в дальнейшем в широкий световой отрезок на оптической оси. Уширение входного пучка (σ = 12,25) приводит к увеличению длины как боковых лепестков, так и фокального светового отрезка с его максимальной длиной DOF = 4,98λ.
Далее рассмотрим поперечные картины дифракции моды Лагерра–супер-Гаусса (1,0) в плоскости xy для всех типов исследуемых кольцевых решеток (в плоскости максимальной вне элемента интенсивности). Результаты исследований для круговой поляризации приведены на рис. 9, для радиальной поляризации – на рис. 10.
Для круговой поляризации размер фокального пятна, формируемый дифракционным аксиконом (с которым проводилось сравнение), был минимальным среди рассмотренных кольцевых решеток: FWHM = 0,58λ (при σ =5 мкм) и FWHM = 0,55λ (при σ = 12,25 мкм).
Для прямой кольцевой решетки основные максимумы формируются внутри элемента, приведенные значения картины дифракции брались в непосредственной близости от элемента. Фокальное пятно для моды Лагерра–супер-Гаусса (1,0) с σ = 5 мкм на 27,5 % (и на 61,8 % для моды Лагерра–супер-Гаусса (1,0) с σ = 12,25 мкм) больше фокального пятна, формируемого дифракционным аксиконом.
Для обратной кольцевой решетки при увеличении размеров входного лазерного пучка также наблюдается уширение размеров фокального пятна по сравнению с фокальным пятном, формируемым дифракционным аксиконом: для моды Лагерра–супер-Гаусса (1,0) с σ = 5 мкм на 60%, а для моды Лагерра–супер-Гаусса (1,0) с σ = 12,25 мкм на 80 %.
Следует отметить, что увеличение размера лазерного пучка при круговой поляризации для дифракционного аксикона приводило к уменьшению размера фокального пятна, а в случае прямой (или обратной) кольцевых решеток наблюдается обратный случай: фокальное пятно начинает уширяться.
При радиальной поляризации, как ранее упоминалось, для всех типов кольцевых решеток наблюдается первоначальное формирование боковых «лепестков», хотя для некоторых случаев в плоскости максимальной интенсивности можно отметить формирование достаточно широкого фокального пятна (рис. 10 в , д , е ).
Таким образом, для мод Лагерра–супер-Гаусса (1,0) использование прямой и обратной кольцевых решеток не позволило получить компактный размер фокального пятна, меньший, чем формируемый дифракционным аксиконом аналогичного периода.
Тем не менее, интересными выглядят результаты формирования пространственно-неоднородного распределения электрического поля на оптической оси и в области пространства, ее окружающего, для обратной кольцевой решетки при круговой поляри- зации. Разберем в следующем параграфе этот случай подробнее.

Рис. 9. Двумерная картина дифракции мод Лагерра–супер-Гаусса (1,0) с круговой поляризацией на кольцевых решетках переменной высоты в плоскости x y, общая интенсивность (размер области - 13,5Х х 13,5Х)
3. Оптическая ловушка для случая обратной кольцевой решетки
Оптический пинцет («оптическая ловушка») [47] позволяет манипулировать микроскопическими объектами с помощью лазерного света и активно используется для биологических и биофизических исследований [48].
Ранее было показано (рис. 7 е ), что для обратной кольцевой решетки для моды Лагерра–супер-Гаусса (1,0) при круговой поляризации наблюдается пространственно-неоднородное распределение электрического поля на оптической оси и в области пространства, ее окружающего, что можно использовать для расширения возможностей оптических пинцетов. Рассмотрим этот случай подробнее (рис. 11).
Максимальная высота пиков интенсивности на оптической оси в продольной плоскости составляет 94,8 % и 62,3 % (рис. 11б), при этом DOF1 = 1,93λ, DOF2 = 3,32λ (по 31,15% от максимальной интенсив- ности). Длина области пониженной интенсивности L= 1,7λ.
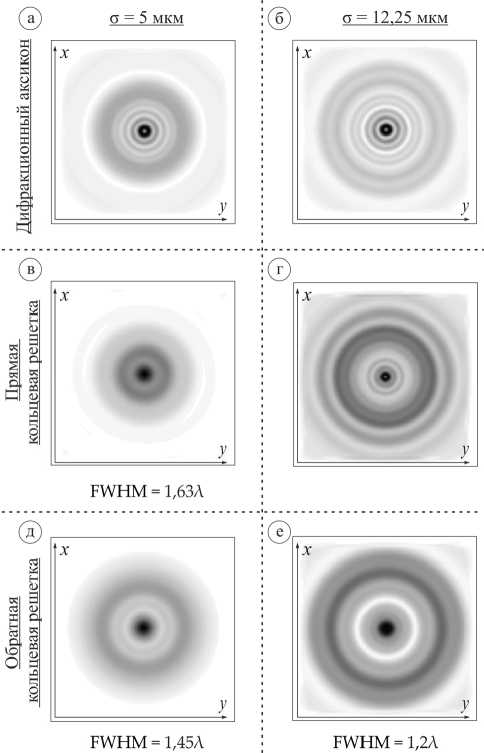
Рис. 10. Двумерная картина дифракции мод Лагерра–супер-Гаусса (1,0) с радиальной поляризацией на кольцевых решетках переменной высоты в плоскости x y, общая интенсивность (размер области - 13,5Х х 13,5Х)
Минимум интенсивности формируется на расстоянии 3,9λ от центра элемента (~11,5% от максимальной интенсивности). Рассмотрим картину дифракции в плоскости минимума интенсивности на оптической оси (рис. 11 г ). Формируется кольцо с пиком, равным 71 % от максимальной интенсивности. Ширина кольца равна FWHM=0,49λ. Ширина теневого фокального пятна (минимум в центре) равна FWHM=0,25λ.
Таким образом, при освещении обратной кольцевой решетки модой Лагерра–супер-Гаусса (1,0) с σ = 12,25 мкм при круговой поляризации наблюдается формирование узкой (FWHM=0,25λ) и протяженной (L= 1,7λ) области пониженной интенсивности на оптической оси.
Заключение
В данной работе методом конечных разностей во временной области было проведено исследование особенностей фокусировки супер-Гауссова пучка, а также мод Лагерра–супер-Гаусса (1,0) с радиальной и круговой поляризациями на кольцевых решетках с переменной высотой колец рельефа и дифракционном аксиконе. Было показано, что направление изменения высоты колец рельефа элементов существенным образом влияет на дифракционную картину в ближней зоне: для отдельных случаев было показано значительное уменьшение размеров фокального пятна, а также формирование оптической ловушки. Поэтому рассмотренные элементы могут иметь практическое применение.
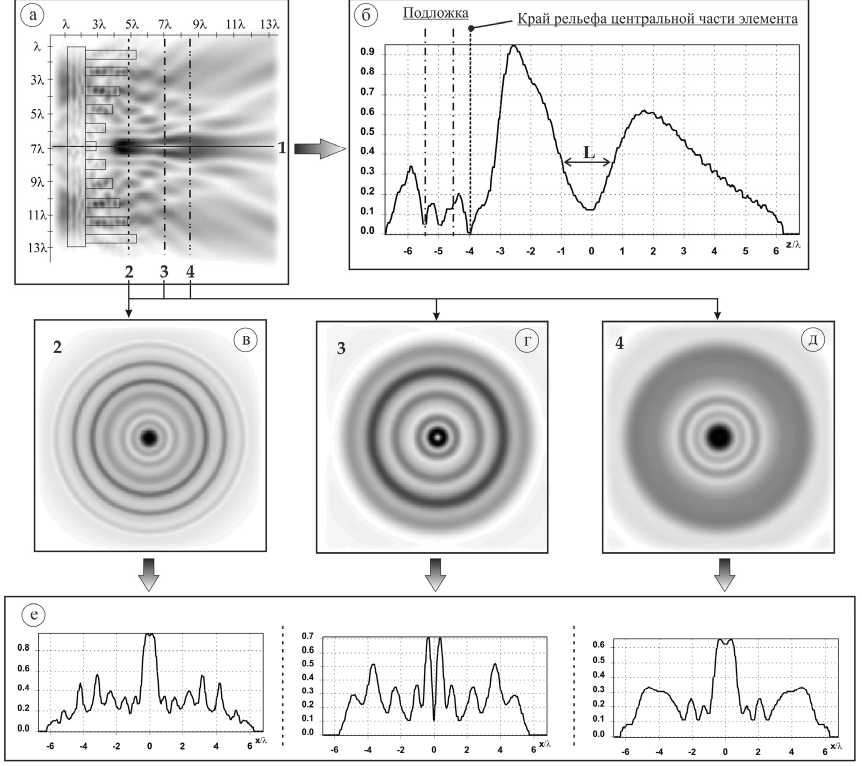
Рис. 11. Двумерная картина дифракции моды Лагерра–супер-Гаусса (1,0) с круговой поляризацией (σ = 12,25 мкм), общая интенсивность (размер области - 13,5Х х 13,5Х): в плоскости xz (a), в плоскости xу (в, г, д), с соответствующими графиками сечений (б, е)
Анализ картины интенсивности электрического поля показал, что наименьший размер фокального пятна при круговой поляризации лазерного излучения был получен для супер-Гауссова пучка (FWHM=0,58λ) для обратной кольцевой решетки, что лучше действия дифракционного аксикона на 31,7 % для лазерного пучка с σ = 5 мкм и на 36,9 % лучше для пучка с σ = 12,25 мкм соответственно.
Для радиальной поляризации наименьший размер фокального пятна был получен также для суперГауссова пучка (при σ =5 мкм) в случае прямой кольцевой решетки в непосредственной близости от элемента: FWHM = 0,39λ, что на 18,7 % лучше, чем действие дифракционного аксикона.
Для мод Лагерра–супер-Гаусса (1,0) использование прямой и обратной кольцевых решеток не позволило получить размер фокального пятна, меньший, чем формируемый дифракционным аксиконом аналогичного периода. Но было показано, что при освещении обратной кольцевой решетки модой Лагерра–супер-Гаусса (1,0) с σ = 12,25 мкм с круговой поляризацией наблюдается формирование узкой (FWHM=0,25λ) и протяженной (L= 1,7λ) области пониженной интенсивности на оптической оси (оптической ловушки).
Работа выполнена при поддержке Министерства науки и высшего образования в рамках выполнения Государственного задания (проект № 0777-20200017) в части «Введение» и Российского научного фонда (проект № 20-72-00051) в остальных частях.
Список литературы Особенности фокусировки супер-гауссовых пучков с круговой и радиальной поляризациями на кольцевых решетках с переменной высотой колец рельефа
- Kotlyar VV, Kovalev AA. Topological charge of optical vortices devoid of radial symmetry. Computer Optics 2020; 44(4): 510-518. DOI: 10.18287/2412-6179-C0-719.
- Zhan Q. Cylindrical vector beams: from mathematical concepts to applications. Adv Opt Photonics 2009; 1: 1-57. DOI: 10.1364/AOP.1.000001.
- Volotovskiy SG, Karpeev SV, Khonina SN. Algorithm for reconstructing complex coefficients of Laguerre-Gaussian modes from the intensity distribution of their coherent superposition. Computer Optics 2020; 44(3): 352-362. DOI: 10.18287/2412-6179-C0-727.
- Savelyev DA, Khonina SN, Golub I. Tight focusing of higher orders Laguerre-Gaussian modes. AIP Conf Proc 2016; 1724: 020021. DOI: 10.1063/1.4945141.
- Hamazaki J, Morita R, Chujo K, Kobayashi Y, Tanda S, Omatsu T. Optical-vortex laser ablation. Opt Express 2010; 18(3): 2144-2151. DOI: 10.1364/OE.18.002144.
- Mourka A, Baumgartl J, Shanor C, Dholakia K, Wright EM. Visualization of the birth of an optical vortex using diffraction from a triangular aperture. Opt Express 2011; 19(7): 5760-5771. DOI: 10.1364/OE.19.005760.
- Tkachenko G, Chen M, Dholakia K, Mazilu M. Is it possible to create a perfect fractional vortex beam? Optica 2017; 4(3): 330-333. DOI: 10.1364/OPTICA.4.000330.
- Khonina SN, Porfirev AP. Harnessing of inhomogeneously polarized Hermite-Gaussian vector beams to manage the 3D spin angular momentum density distribution. Nanophotonics 2021; 11(4): 0418. DOI: 10.1515/nanoph-2021-0418.
- LiS, Pan X, Ren Y, Liu H, Yu S, Jing J. Deterministic generation of orbital-angular-momentum multiplexed tripartite entanglement. Phys Rev Lett 2020; 124(8): 083605. DOI: 10.1103/PhysRevLett.124.083605.
- Ma X, Pu M, Li X, Huang C, Wang Y, Pan W,Zhao B, Cui J, Wang Ch, Zhao Z, Luo X. A planar chiral meta-surface for optical vortex generation and focusing. Sci Rep 2015; 5(1): 10365. DOI: 10.1038/srep10365.
- Pryamikov A, Alagashev G, Falkovich G, Turitsyn S. Light transport and vortex-suppoted wave-guiding in micro-structured optical fibers. Sci Rep 2020; 10(1): 2507. DOI: 10.1038/s41598-020-59508-z.
- Khonina SN, Alferov SV, Karpeev SV. Strengthening the longitudinal component of the sharply focused electric field by means of higher-order laser beams. Opt Lett 2013; 38(17): 3223-3226. DOI: 10.1364/OL.38.003223.
- Savelyev DA, Khonina SN. Characteristics of sharp focusing of vortex Laguerre-Gaussian beams. Computer Optics 2015; 39(5): 654-662. DOI: 10.18287/0134-2452-2015-395-654-662.
- Zhu L, Wang J. A review of multiple optical vortices generation: methods and applications. Front Optoelectron 2019; 12(1): 52-68. DOI: 10.1007/s12200-019-0910-9.
- Khonina SN. Vortex beams with high-order cylindrical polarization: features of focal distributions. Appl Phys B 2019; 125: 100. DOI: 10.1007/s00340-019-7212-1.
- Khonina SN, Porfirev AP, Kazanskiy NL. Variable transformation of singular cylindrical vector beams using aniso-tropic crystals. Sci Rep 2020; 10: 5590. DOI: 10.1038/s41598-020-62546-2.
- Khonina SN, Golub I. Engineering the smallest 3D symmetrical bright and dark focal spots. J Opt Soc Am A 2013; 30(10): 2029-2033. DOI: 10.1364/JOSAA.30.002029.
- Savelyev DA. The investigation of focusing of cylindrical-ly polarized beams with the variable height of optical elements using high-performance computer systems. Proc SPIE 2021; 11793: 117930X. DOI: 10.1117/12.2591993.
- Khonina SN, Karpeev SV, Alferov SV, Soifer VA. Generation of cylindrical vector beams of high orders using uniaxial crystals. J Opt 2015; 17(6): 065001. DOI: 10.1088/2040-8978/17/6/065001.
- Fu S, Gao C, Wang T, Zhai Y, Yin C. Anisotropic polarization modulation for the production of arbitrary Poincare beams. J Opt Soc Am B 2018; 35(1): 1-7. DOI: 10.1364/JOSAB.35.000001.
- Fadeyeva T, Shvedov V, Shostka N, Alexeyev C, Volyar A. Natural shaping of the cylindrically polarized beams. Opt Lett 2010; 35(22): 3787-3789. DOI: 10.1364/OL.35.003787.
- Khonina SN, Karpeev SV, Paranin VD, Morozov AA. Polarization conversion under focusing of vortex laser beams along the axis of anisotropic crystals. Phys Lett A 2017: 381(30): 2444-2455. DOI: 10.1016/j.physleta.2017.05.025.
- Savelyev D. The investigation of the cylindrically polarized beams focusing by a diffractive axicon using highperformance computer systems. 2020 Int Conf on Information Technology and Nanotechnology (ITNT) 2020: 15. DOI: 10.1109/ITNT49337.2020.9253243.
- Wang H, Shi L, Lukyanchuk B, Sheppard C, Chong CT. Creation of a needle of longitudinally polarized light in vacuum using binary optics. Nat Photonics 2008; 2(8): 501-505. DOI: 10.1038/nphoton.2008.127.
- Kozawa Y, Sato S. Sharper focal spot formed by higherorder radially polarized laser beams. J Opt Soc Am A 2007; 24(6): 1793-1798. DOI: 10.1364/JOSAA.24.001793.
- Sheppard CJ, Choudhury A. Annular pupils, radial polarization, and superresolution. Appl Opt 2004; 43(22): 43224327. DOI: 10.1364/AO.43.004322.
- Kotlyar VV, Stafeev SS. Modeling the sharp focus of a radially polarized laser mode using a conical and a binary microaxicon. J Opt Soc Am B 2010; 27(10): 1991-1997. DOI: 10.1364/JOSAB.27.001991.
- Khonina SN, Degtyarev SA. A longitudinally polarized beam generated by a binary axicon. J Russ Laser Res 2015; 36(2): 151-161. DOI: 10.1007/s10946-015-9488-x.
- Lerman GM, Levy U. Effect of radial polarization and apodization on spot size under tight focusing conditions. Opt Express 2008; 16(7): 4567-4581. DOI: 10.1364/OE.16.004567.
- Dorn R, Quabis S, Leuchs G. Sharper focus for a radially polarized light beam. Phys Rev Lett 2003; 91(23): 233901. DOI: 10.1103/Phy sRevLett.91.233901.
- Khonina SN, Volotovsky SG. Controlling the contribution of the electric field components to the focus of a high-aperture lens using binary phase structures. J Opt Soc Am A 2010; 27(10): 2188-2197. DOI: 10.1364/JOSAA.27.002188.
- Pereira SF, Van de Nes AS. Superresolution by means of polarisation, phase and amplitude pupil masks. Opt Commun 2004; 234(1-6): 119-124. DOI: 10.1016/j.optcom.2004.02.020.
- Chen Z, Hua L, Pu J. Tight focusing of light beams: effect of polarization, phase, and coherence. In Book: Wolf E, ed. Progress in Optics. Ch 4. Oxford: Elsevier; 2012: 219-260. DOI: 10.1016/B978-0-44-459422-8.00004-7.
- McLeod JH. The axicon: a new type of optical element. J Opt Soc Am 1954; 44(8): 592-597. DOI: 10.1364/JOSA.44.000592.
- Golub I, Chebbi B, Shaw D, Nowacki D. Characterization of a refractive logarithmic axicon. Opt Lett 2010; 35(16): 2828-2830. DOI: 10.1364/OL.35.002828.
- Savelyev DA. The sub-wavelength complex micro-axicons for focal spot size reducing using high-performance computer systems. Proc SPIE 2021; 11769: 1176918. DOI: 10.1117/12.2589220.
- Chi W, George N. Electronic imaging using a logarithmic asphere. Opt Lett 2001; 26(12): 875-877. DOI: 10.1364/OL.26.000875.
- Khonina SN, Kazanskiy NL, Khorin PA, Butt MA. Modern types of axicons: New functions and applications. Sensors 2021; 21(19): 6690. DOI: 10.3390/s21196690.
- Savelyev D, Kazanskiy N. Near-field vortex beams diffraction on surface micro-defects and diffractive axicons for polarization state recognition. Sensors 2021; 21(6): 1973. DOI: 10.3390/s21061973.
- Savelyev DA. The investigation of the features of focusing vortex super-Gaussian beams with a variable-height diffractive axicon. Computer Optics 2021; 45(2): 214-221. DOI: 10.18287/2412-6179-C0-862.
- Savelyev DA. The comparison of laser radiation focusing by diffractive axicons and annular gratings with variable height using high-performance computer systems. 2021 Photonics & Electromagnetics Research Symposium (PIERS) 2021: 2709-2716. DOI: 10.1109/PIERS53385.2021.9694860.
- Savelyev D. Diffraction of vortex beams by annular gratings with variable height in the near zone. 2021 International Conference on Information Technology and Nano-technology (ITNT) 2021: 1-6. DOI: 10.1109/ITNT52450.2021.9649245.
- Prather DW, Shi S. Formulation and application of the finite-difference time-domain method for the analysis of axially symmetric diffractive optical elements. J Opt Soc Am A 1999; 16(5): 1131-1142. DOI: 10.1364/JOSAA.16.001131.
- Oskooi AF, Roundy D, Ibanescu M, Bermel P, Joannopou-los JD, Johnson SG. MEEP: A flexible free-software package for electromagnetic simulations by the FDTD method. Comput Phys Commun 2010; 181(3): 687-702. DOI: 10.1016/j.cpc.2009.11.008.
- Ding X, Ren Y, Lu R. Shaping super-Gaussian beam through digital micro-mirror device. Sci China Phys Mech 2015; 58(3): 1-6. DOI: 10.1007/s11433-014-5499-9.
- Malik HK, Devi L. Relativistic self focusing and frequency shift of super-Gaussian laser beam in plasma. Results Phys 2020; 17: 103070. DOI: 10.1016/j.rinp.2020.103070.
- Ashkin A, Dziedzic JM, Bjorkholm JE, Chu S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt Lett 1986; 11(5): 288-290. DOI: 10.1364/OL.11.000288.
- Gouesbet G. Generalized Lorenz--Mie theories and mechanical effects of laser light, on the occasion of Arthur Ashkin's receipt of the 2018 Nobel prize in physics for his pioneering work in optical levitation and manipulation: A review. J Quant Spectrosc Radiat Transf 2019; 225: 258277. DOI: 10.1016/j.jqsrt.2018.12.015.


