Особенности функционирования нагруженных резонансных контуров в системах передачи электрической энергии

Введение. Известно, что собственная резонансная частота (<у₀) последовательного (r, L, C) или параллельного (R, L, C) резонансных контуров зависит не только от реактивных компонентов (L, C), но и от величины активных (r, R), [1]. Это обстоятельство обязывает разработчиков резонансных систем передачи электрической энергии принимать определенные меры для снижения степени влияния r, R на резонансные свойства силовых контуров. Часто используется коррекция частоты питающего тока в соответствии с изменением нагрузки [2-4].

Цель исследований. Представляется целесообразным проанализировать характер электрофизических процессов, происходящих в нагружаемых контурах, а так же исследовать саму необходимость коррекции частоты питающего тока при изменении интенсивности нагружения.

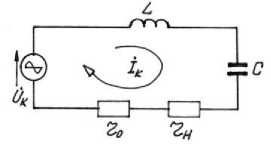
Основная часть. Рассмотрим два контура (рисунок 1.1 и рисунок 1.2). Резонансные частоты приведенных резонансных контуров описываются выражениями 1а и 1b.

(1а)

Рисунок 1.1 – Последовательный резонансный контур с

Г_1_ _ (Гр + Н_Н ) ² 1 2

• I .LC 41? J '

  разделенными активными резисторами r 0 , r H

  

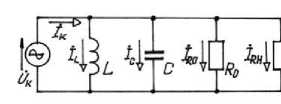
  Рисунок 1.2 – Параллельный резонансный контур с разделенными активными резисторами R 0 , R H .

  
  

, = Г— _ _(^£+± h )2L 1²

L С 4С² (R₀-Н_Н ) ² '

(1b)

Пусть при работе по схеме р исунка 1.1 , с целью охвата всех режимов нагружения от короткого замыкания до холостого хода, сопротивление резистора нагрузки r н изменяется от нуля («закоротка») до бесконечности («разрыв»). При работе по схеме соединений, изображенной на рисунке 1.2, сопротивление резистора нагрузки R н изменяется аналогично.

Частота собственного резонанса при коротком замыкании сопротивления нагрузки в схеме рисунка 1.1 будет равна: O> = ( –

₎ 1/2

4L2).

При устремлении r_н → ∞ наступает разрыв цепи.

При соединении (R, L, C) по схеме рисунка 1.2 резонансная частота при Rн→∞ предстанет как: 0) = (–   ∙ )1/2 . При снижении сопротивления нагрузки Rн до нуля контур рисунка 1.2 перестает работать из-за короткого питания и контура.

(R, L, C) по схеме замыкания источника

1б показывает, что

Сравнение полученных частот 1а и резонансные частоты реальных контуров по рисунку 1.1 при rн =0 («короткое замыкание») и по рисунку 1.2 при Rн → ∞ («холостой ход») представляют собой собственные резонансные частоты, определяемые реактивными компонентами контуров (L, C) и их сопротивлениями потерь (r0, R0).

Дальнейшее преобразование 1а и 1б дает следующее:

to = ( Ге ) ^1/2 (1 – 4L²₎ 1/2 ₌ too (1 – 4 ) ^1/2 , (2а)

(

to = ( Ге ) ^1/2 (1 – 4C² Rn ₎ 1/2 ₌ too (1 – 4R² ) ^1/2 . (2б) LC               л._п                 ^^n

Здесь: (Z)q = ( ) ^1/2 – собственная резонансная угловая частота идеализированного контура без потерь, c ^-1 ,

Z_c – волновое сопротивление резонансного контура, Ом. Z_c = ( ) ^1/2 . Учитывая, что = Q 0 , и Zc^ = Q₀ по определению добротностей последовательного и параллельного резонансных контуров, получают:

to =    (1 – 4Qo )1/2 (3а)

to =     (1 –    ) ^1/2 (3б)

Здесь Q0 – добротность ненагруженного контура.

Соотношения (3) показывают, что выражения для резонансных частот ω, при использовании для их описания добротности Q, у последовательных и у параллельных контуров идентичны. Поэтому далее при анализе резонансных свойств не конкретизируется тип контура.

При нагружении контура резонансная частота ω уменьшаются в соответствии с (1a), (1б).

Из (3) может быть определена минимальная величина добротности Q, при которой контур еще сохраняет резонансные свойства. Потеря резонансных свойств в рассматриваемом случае означает снижение резонансной частоты ω до нуля. В соответствии с этим по (3) 0 = (1 \—) ^1/2 . Предельное значение добротности:

• ⁴ 0 пред

Qпред = 0,5. Для последовательного резонансного контура Q = 0,5

означает достижение активным сопротивлением r контура величины r = -^— = — = 2Z c , Ом. Для параллельного резонансного контура

Q пред ⁰ -

Q = 0,5 означает достижение активным сопротивлением R контура величины R = Zc Qпред = 0,5 Zc, Ом. Поскольку сопротивления нагрузок rн, Rн составляют часть общего активного сопротивления r, R контуров можно записать соотношения сопротивлений в контурах следующим образом:

Г о + Г н = r < 2Z c ,

К 0 ^А н

R 0+R н

= R> 0,5Z c .

И далее:

для последовательного контура r_H< 2Z c - r₀ = Z c , (4a)

(

T>       0- 5 А 0 ^C    ry Qo для параллельного контура Rh > ------= Zc---- , 4)

R o~ 0,5 C_c       2 ^Q o~ 1

(4b)

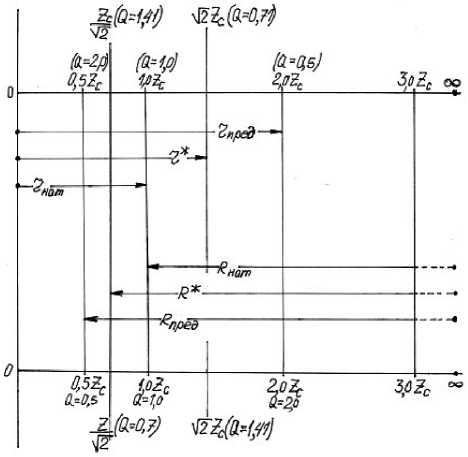
Полученный результат может быть представлен в виде диаграммы ( рисунок 2 ).

Диаграмма показывает, что разрешенные режимы работы последовательного резонансного контура располагаются в диапазоне 0H<г_пред , где г_пред = (2Z_c - r₀). Режимы работ параллельного резонансного контура располагаются справа от R_пред, т.е. R_пред< R_H , ⁵ R o c_c

• <^{( да} ), ^{где R} пре _д = _       .

А 0 “ 0,5 c

Справа от r_пре д , т.е. при r> r_пред, последовательный контур теряет резонансные свойства. Для параллельного контура аналогичная ситуация наступает при R< R_пред, где параллельный контур так же теряет резонансные свойства.

На диаграмме выявлен режим эквивалентного нагружения, при котором электрофизические состояния контуров идентичны. Это имеет место при нагружении на сопротивление равное волновому, т.е. при r =R =Z c . Такой режим для последовательных и параллельных контуров называют натуральным.

При натуральном нагружении rнат=Rнат=Zc добротности контуров становятся равными Q=1,0 и напряжения на реактивных компонентах

напряжению токи.

последовательного контура становятся равными генератора, в параллельном контуре сравниваются все

Область

« разреш енных » сопротивлений последовательного резонансного контура

Область

«разреш енных» с огротивл ений параллельного резонансного контура

Рисунок 2 – Диаграмма областей сопротивлений нагрузок последовательного и параллельного контуров. Сопротивления на границах областей округлены до r Н =2Z C , R Н =0,5Z C

Из диаграммы следует, что ни параллельный ни последовательный контур не обеспечивают возможность работы при нагружении в непрерывно изменяющемся диапазоне величин сопротивления нагрузки от 0 («короткого замыкания») до ∞ («холостого хода»).

Если технические требования однозначно предписывают необходимость обеспечения диапазона перекрытия сопротивления нагрузок от «нуля» («Короткое замыкание») до «разрыва» («Холостой ход»), то диаграмма «разрешает» совершить в точке rнат = Rнат = Zс переход (переключение) из одного типа соединения, например, последовательного, в другой, соответственно, параллельный. И наоборот, перейти от схемы параллельного соединения к схеме последовательного.

На рисунках 3.1, 3.2, 3.3 приведен пример переключения последовательного резонансного контура (L, C, r) в параллельный резонансный контур (L, C, R) одним «щелчком» сдвоенного переключателя (П1.1, П1.2). На рисунках 3 разъяснена технология «перехода» (L, C, r) в (L, C, R). Переход удобно производить с помощью электронных ключей в момент прохождения тока через нуль.

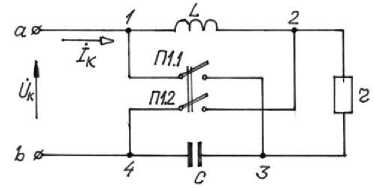
Рисунок 3.1 – Принципиальная схема соединения электрических компонентов последовательного резонансного (L, C, r) контура и сдвоенного переключателя (П 1.1, П 1.2). Перемычки разомкнуты.

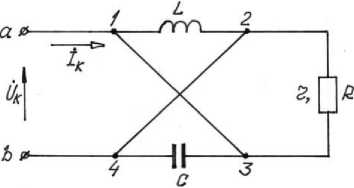
Рисунок 3.2 – Принципиальная схема включения электрических перемычек (1-3) и (2-4), перемыкание приводит к переводу последовательного (L, C, r) контура в параллельный (L, C, R) контур.

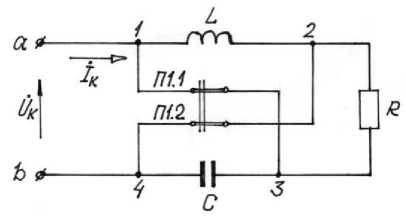
Рисунок 3.3 - Принципиальная схема соединения электрических

компонентов параллельного резонансного(Е, C, R) сдвоенного выключателя (П 1.1, П 1.2). Перемычки (П замкнуты

Для выяснения необходимости коррекции частоты контура и 1.1, П 1.2)

питающего

тока при нагружении контура исследуем частотную зависимость входного сопротивления (импеданс) последовательного резонансного контура (L, C, r) по рисунку 1.1 . Входное сопротивление контура равно:

z = [г² + ( ш-- ^) ² ] ^1/2 . (5)

Здесь: to - круговая частота переменного тока генератора, питающего последовательный резонансный контур (L, C, r).

При изменении частоты to ток контура Ik меняется в соответствии с изменением входного сопротивления z.

Преобразуем (5):

^z- = [1+ Q₀ ² (^- - ^) ² ] ^1/2 (6)

Здесь: to0 - собственная резонансная частота ненагруженного (идеализированного) контура, to0= (—) й;

Q₀ = добротность контура на собственной резонансной частоте ^to о .

Таким образом, получаем: Q₀ = ^—¹ = ^-^ = ^ = ( | ) ^1/2 р

Если представить текущее значение частоты ш в относительных величинах =  , частотная зависимость относительного импеданса

"о

• (6) предстанет в следующем виде: - = [1+ Q₀ ² (to _г--) ² ] ^1/2 .

т _̇

При этом ток контура i_k = ~ . Напряжение на активном сопротивлении потерь г₀ составит U _r0 = i_k г₀. Напряжение на нагрузочном резисторе г_н: U_н = i_k г_н = U_к у.

На рисунке 4 представлены частотные зависимости токов последовательного условного контура (L,C), нагруженного на активные сопротивления четырех номиналов, таких, что при условном характеристическом сопротивлении контура Z c =(|;) ^1/2 =10 Ом, его добротности равнялись:

Q 1 = 10 при r = 1,0 Ом,

Q 2 = 5 при r = 2,0 Ом,

Q 4 = 2,5 при r = 4,0 Ом,

Q 5 = 1,0 при r = 10 Ом.

На графиках рисунке 4 частота представлена в виде относительной со — — — в диапазоне 0< со ₁<  1,5.

ш0

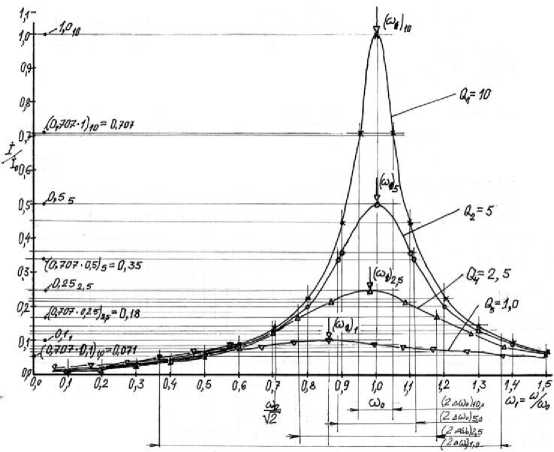
Рисунок 4 – Частотные зависимости токов последовательного резонансного контура при различных нагружениях

По оси ординат отложены токи Ỉ k последовательных контуров (L,C,r). Предварительно токи пронормированы по отношению к резонансному току İ 0 при максимальной добротности Q = 10 (r = 1,0 Ом). При токах İ=0,707Ỉ 0 определены значения частот верхнего и нижнего края полосы пропускания. Для резонансной кривой при Q = 10 полоса составила 2(Д со ) = ^— .

Полосы и добротности контуров при нагружении другими сопротивлениями составили:

при Q 2 = 5 и r = 2,0 Ом полоса → 2(Δ О) )₂ ;

при Q 4 = 2,5 и r = 4,0 Ом полоса → 2(Δto) 4 ;

при Q 5 = 1,0 и r = 10,0 Ом полоса → 2(Δto)₅.

Графики показывают, что при нагружении контура имеет место «уход» (снижение) резонансной частоты в соответствии с (7). Снижение резонансной частоты Δ( О) ) =( 60q _- О) ) при нагружении и соответствующие полосы пропускания в относительном представлении б = ^{(Δ )} в зависимости от добротности Q приведены в ш₀

таблице 1.

Таблица 1 – Зависимость снижения резонансной частоты Δ и "о относительных полос пропускания (Δ ) от добротности Q

Добротность, Q	-	0,5	0,707	1,0	2,5	5,0	10
Уход частоты резонанса при нагружении	Δ (У ^0	100	29	13,4	2,0	0,5	0,1
Относительная полоса пропускания	2(Δ to ) too	200	140	100	40	20	10

Частотные зависимости токов Ỉk последовательного резонансного контура при различных нагружения рассчитаны по:

İ_k = ^ = ̇ к [r ² + Z c ² ( - ^) ² ] ^1/2 . (7) Л *-^О ^

Графики на рисунке 4 показывают, что в режиме интенсивного нагружения, вплоть до добротностей порядка единицы в резонансных контурах, кроме снижения частоты резонанса, происходит резкое снижение тока из-за падения добротности.

Из приведенного следует, что приоритетной задачей управления является необходимость стабилизации напряжения на выходе резонансной системы. При этом хорошо видно, что удержание выходной частоты генератора на резонансной частоте контура способствует «удержанию» напряжения в существенно меньшей степени и поэтому может быть исключено. Кроме этого при работе с коррекцией частоты питающего тока требуется существенно большая полоса частот, что может оказаться недопустимым, по коммерческим соображениям.

На практике бывает необходимо синтезировать схему с током на входе (İ k ), не изменяющимся по модулю при большом диапазоне вариации сопротивления нагрузки 0 < г_н<  да . Реально это означает

независимость модуля входного тока от изменения режима нагружения от «короткого замыкания» до «холостого хода».

В классическом исполнении ни последовательный, ни параллельный резонансные контуры подобную задачу не решают ( рисунок 2 ).

Рассмотрим возможности   параллельно-последовательного контура (рисунок 5).

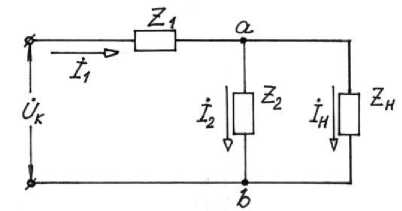
Рисунок 5 – Параллельно-последовательный контур (контур со смешанным соединением элементов)

Элементы контура представлены в общем виде. Входное сопротивление такого контура равно:

Z вх = Z 1 + Z ab .

Здесь: Z_ab – входной импеданс участка (a,b), представляющего собой параллельно включенные Z₂ и Z_н . Сопротивление Z_ab может быть определено через сумму проводимостей параллельных ветвей Z₂ и Z н :

5 = Y -b = Y 2 + ^Y - = Н + i = ^,

где Y – проводимость, Ом.

Поскольку Z ab = ^ , учитывая (9), получаем:

Z н Z 2

Z= ^ab          н

.

Подставив (10) в (8), получаем входное сопротивление контура:

_Z 1 (Z 2 + Z н ) + Z 2 • Z h

Z_вх = Z₁ + Z_a b =

Z 2+Z н

.

Для выявления режима, обеспечивающего независимость

величины модуля входного тока İ1 от предварительно исследуем модуль Zвх. преобразование схемы соединений по

сопротивления нагрузки, Для этого выполним рисунку 5 в схему

последовательного соединения элементов по рисунку 6 , упрощающего вычисления и обеспечивающего бόльшую наглядность.

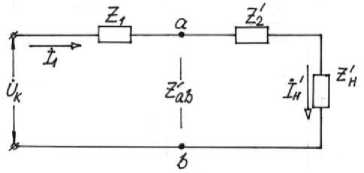
Рисунок 6 – Преобразование параллельного соединения на участке сопротивлений Z2 и Zн в эквивалентное, последовательное соединение сопротивлений (Z2’ и Zн’).

Преобразование произведено таким образом, чтобы входной импеданс между точками (a,b) оставался неизменным Z_ab≡ Z_ab ^' .

В соответствии с (10) сопротивление Z ab в схеме по рисунку 6

Z ^н Z2 равно Z ab =

н

.

Входной импеданс всей схемы после Z вх ʹ = Z 1 +Z 2^' + R н ^' будет равен:

преобразования

Zвхʹ = +j to L – j ti)L^l+ti)^Rн■c2Vrн MC . (12) l+ca2Rн        . (12)

Преобразования (12) обычный характер и дают:

Rн a>C             Rн н + н

1+ш²Я н c²     1+ш²Я н c²

нн

Rн

+ j l + w2Rн C2      J

в направлении получения |Zвх| носят

|Z вх | = |Z вх^' |= [ - н ( l-2to²LC ) ₊ (o²L² _] 1/2 _н

.

Анализ (13) показывает, что на частоте питающего тока =

1   ^ -                                               I ™qL

= модуль импеданса становится равным | _√ | и не зависит от R_н. Ток |İ 1 | не зависит от R н и равен

|İ | = ^Ù = ^√2 Ù

|İ 1 | =      =

.

Здесь Z_с характеристическое сопротивление, Z_с = ( ) 1/2

=    =

С

В справедливости (14) можно убедиться путем прямой подстановки найденной частоты CO =(2 LC ₎ –1/2 = _√ в (13):

|Z вх^' |= [ ^{5 н (}     н s ⁾

+ to²L² _] 1/2

= [

R _{н (} ^ЧГс ⁾ l+to²Rн c²

+ ^o £2]1/2

+      ] = √2

'

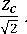
При изменении R_н у Z_вх изменяется только фаза cos ф. При питании током с частотой ^= схема позволяет изменять фазу вектора

входного тока без изменения его величины. Напряжение индуктивности L равно по величине U ^ и опережает ток i 1 на тт/2.

Определим величину нагрузочного сопротивления

на

сдвигающего частоту собственного резонанса ш 0 до значения

Расчет можно выполнить с помощью (2):

= Щ ₀[1 - Д] ^1/2 .

√                _н

Вычисления показывают, что R Н = ^| и г*= 42 Z_с .

Оба сопротивления показаны на диаграмме сопротивлений нагрузок резонансных контуров ( рис.2 ).

RH, i

to = 1= √

.

областей

Режимы

нагружения на г* и R* лежат между предельными режимами существования свободных колебаний (г_н =2 Z_c, R_H=0,5 Z_c ) и режимом натурального нагружения (г_н = 1,0 Z_c, R_н = 1,0 Z_c)

Таким образом, применение резонансных, последовательного либо параллельного контуров, с целью подъема напряжения в системах передачи электрической энергии малоэффективно, так как

при нагружении изменяются в сторону уменьшения не только резонансная частота контура, но и добротность. Влияние снижения добротности оказывается чрезвычайно интенсивным, что приводит к необходимости обязательной стабилизации напряжения на выходе системы передачи. Одновременно корректировать частоту питающего тока с целью коррекции напряжения на выходе системы представляется нецелесообразным. Более того и противоестественно, поскольку работа с корректировкой частоты означает работу в более широкой полосе частот. Необходимая ширина полосы может достигать половины рабочей частоты. Просматривается более предпочтительный алгоритм настройки и управления генератором. Генератор настраивается на частоту системы передачи, предварительно нагруженной на натуральную или максимальную из предполагаемых нагрузок, после чего частота генератора фиксируется и настраиваются цепи обратной связи для стабилизации напряжения на выходе системы передачи энергии. Все дальнейшие манипуляции исключаются. Система передачи при эксплуатации ведет себя следующим образом. На холостом ходу (нагрузка снята) добротность резонансной части системы передачи высокая, но частота питающего тока ниже резонансной, поэтому резкий подъем напряжения на выходе системы отсутствует, а следовательно, отпадает необходимость в «балластных» поглотителях энергии, как это сделано в [2, 3] По мере нагружения контура его добротность понижается, а резонансная частота контура системы передачи приближается к частоте питающего тока, что запускает в действие механизм подъема напряжения за счет резонанса.

Рассмотренные аспекты поведения резонансных контуров с сосредоточенными параметрами при их нагружении относятся к случаям работы контуров вне особых требований к контурам со стороны иных схемотехнических компонентов энергетических систем. Однако, часто это условие не выполняется.

Например, при работе резонансного контура в составе преобразователя частоты. Обычно в системах с преобразователями стараются избегать применения реактивных компонентов, склонных автономно или в совокупности с другими компонентами, к резонансу. Если питаемое от преобразователя устройство функционирует на принципе электрического резонанса и в некоторых других случаях, (L, C) - композиции охотно используются. Например, при питании закалочных или плавильных индукторов, сушильных агрегатов, паяльных автоматов и другое [4-6].

Особенно широко используются резонансные контуры со смешенными соединениями L, C, R. В [5] выполнен анализ энергетических характеристик преобразователя частоты при его согласовании с изменяющейся нагрузкой при помощи последовательно - параллельного резонансного контура. Показано, что изменение активной составляющей нагрузки не всегда приводит к пропорциональному изменению входного сопротивления резонансного контура, причем на определенных частотах резонансный контур имеет фактически постоянное входное сопротивление при изменении нагрузки в существенно отличающихся пределах, что однозначно перекликается с эффектом, описанным в настоящей статье. Автор [5] столкнулся с эффектом параметрической стабилизации, в определенном смысле, случайно, в предлагаемой статье авторы вышли на этот режим путем решения целенаправленно поставленной задачи. Этот факт дает возможность с большей уверенностью считать выявленный эффект (параметрическая стабилизация) объективным и заслуживающим более тщательного изучения.

Большие возможности демонстрируют контура с резонансными параметрами второго и более высоких порядков [6-9].

Необходимо отметить, резонансные системы на элементах с распределенными электрическими параметрами (распределенная индуктивность, распределенная емкость) [10] могут работать без проблем при широком диапазоне изменения сопротивления нагрузки [11], [12] как в оборудовании, работающем с использованием электрического резонанса, так и в оборудовании для технологий с сугубо электрической специализацией [13].

Заключение

• 1.    При нагружении резонансного контура его собственная резонансная частота снижается вплоть до нуля при достижении сопротивлением нагрузки критической величины.

• 2.    Следствием «ухода» частоты при нагружении резонансного контура является снижение напряжения на выходе системы. Для компенсации снижения напряжения на выходе системы предпочтительней применять механизм автоматического поддержания напряжения, нежели коррекцию частоты питающего тока. При этом бывает часто более эффективным приемом: питание током с упрежденно сниженной частотой.

• 3.    Энергетическая пропускная способность параллельного и последовательного контуров ограничивается характеристическими сопротивлениями.

• 4.    Работа контуров на частоте резонанса приводит к возникновению на выходе системы аварийноопасных выбросов напряжения при снижении нагрузки и особенно при ее отключении.

• 5.    Ни параллельный, ни последовательный контуры не обеспечивают диапазон перекрытия сопротивления нагрузки от нуля до бесконечности (непрерывное изменение нагружения от короткого замыкания до холостого хода).

• 6.    Для обеспечения режима работы резонансной системы с перекрытием диапазона сопротивлений от К3 до ХХ необходимо организовать переход системы из последовательного соединения реактивных компонентов в параллельное и наоборот, с переходом системы через натуральный режим нагружения, либо использовать смешанное соединение реактивных компонентов системы и нагрузки.

• 7.    При смешанном соединении компонентов контура появляется режим питания (на частоте питающего тока (л) = _√ ), при котором модуль входного сопротивления системы не зависит от величины нагрузки, чем обеспечивается возможность изменения её в диапазоне от короткого замыкания до холостого хода. При изменении нагрузки изменяется только фаза входного тока по отношению к питающему напряжению.

• 8.    Работа резонансной системы с коррекцией частоты питающего тока требует существенно более широкого диапазона разрешенных частот.

SPECIFICITIES OF THE FUNCTIONING OF THE LOADED RESONANT CIRCUITS IN TRANSMISSION SYSTEMS OF

Federal State Budgetary Scientific Institution "Federal Scientific Agroengineering Center VIM" (FSAC VIM), 1st Institutsky proezd, 5, Moscow, 109428 Russian Federation