Особенности гексагональных клеточных автоматов на плоской поверхности для задач нанотехнологии
Автор: Матюшкин И.В., Коробов С.В., Вильданов Р.Р.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Нанофизика и нанотехнологии
Статья в выпуске: 1 (21) т.6, 2014 года.
Бесплатный доступ
Приведены результаты вычислительных экспериментов в программе SoftCAM с клеточными автоматами тоталистичного типа на гексагональной сетке. Даны некоторые смысловые интерпретации в контексте нанотехнологий.
Клеточные автоматы, поверхность, нанотехнология, гексагональная сетка, граница, автомат фредкина
Короткий адрес: https://sciup.org/142185981
IDR: 142185981 | УДК: 621.391.1:004
Текст научной статьи Особенности гексагональных клеточных автоматов на плоской поверхности для задач нанотехнологии
Несмотря на. то, что теория клеточных автоматов (КА) известна, с 40-х гг. XX века, она стала активно использоваться в микроэлектронике лишь в последние 10-15 лет. Это относится прежде всего к моделированию физико-химических процессов, в частности диффузии [1], протекания жидкости [2], разделения фаз [3] и кристаллизации, образования пор [4] и развития дислокаций [5]. В задачах нанотехнологии все чаще приходится сталкиваться с искривленными поверхностями и сложными структурами, которые трудно описать обычными методами вычислительной математики.
Гексагональные сетки (ГС) необходимо использовать для процессов, в которых важна. изотропность, например, в задачах гидродинамики, газодинамики и диффузии [2]. Принципиальную трудность при моделировании сложных физико-химических процессов представляет анализ явлений конденсации, кипения, кавитации. Это связано с возникновением большого числа, границ раздела, что ставит под сомнение адекватность описания таких процессов разностными схемами для уравнений в частных производных.
Целью данной работы является построение и изучение различных КА на ГС, которые потенциально могут быть использованы для моделирования реальных физико-химических процессов на. поверхности твёрдого тела.
Построение гексагональных сеток
Метод КА реализуется на. трёх типах регулярных сеток: треугольной, квадратной и гексагональной. Несмотря на. то, что первые две обладают высокой скоростью вычислений при численных расчётах [6], последняя имеет однородность в моделируемом пространстве и облегчает приближение численной схемы к физическому смыслу модели. На рис. 1 показан фрагмент ГС с кольцами, в каждой клетке указана, пара, декартовых координат.
Рис. 1. Кольца, для ГС
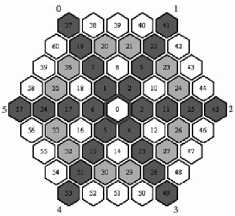
Рис. 2. Спиральные обобщенные координаты для ГС
Клетка, является элементом (соседом) нулевого кольца, для самой себя, её соседи - элементами первого кольца. Далее - рекурсивно: для данной клетки элементами г-го кольца
(кольца Тго порядка) называются все клетки, являющиеся соседями какой-либо клетки ее (г-1)-го кольца, исключая те из них, которые сами принадлежат кольцам меньших порядков. Также возможно использование спиральных обобщенных координат, введенных Наумовым Л.А. [7]. Некоторой клетке присваивается координата ноль. Далее, начиная с левого верхнего угла по часовой стрелке последовательно нумеруются клетки ее колец. Результат показан на рис. 2.
ГС обладают лучшей адаптивностью, чем квадратная или треугольная сетки, но при этом и пониженной скоростью работы. Но эту проблему можно решить, используя реконфигурируемые шаблоны [8]. На рис. За представлен двухтактный шаблон. На каждом шаге по очереди используется один из двух вариантов соседства. На рис. 36 - соответственно трехтактный. Производительность автомата на ГС с реконфигурируемым шаблоном превышает производительность аналогичного автомата без реконфигурируемого шаблона в среднем на 30%.

Рис. 3. Реконфигурируемые шаблоны для клеточного автомата, на. ГС: а. - двухтактный; б - трехтактный
Существующие KA-модели физико-химических процессов на ГС
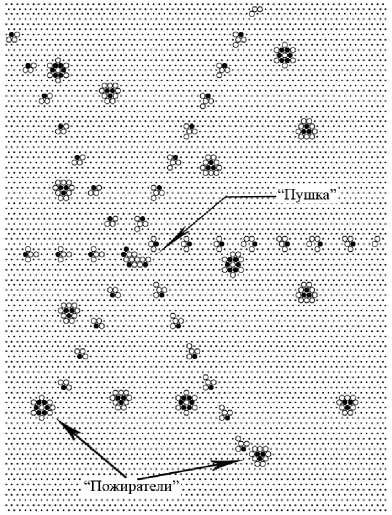
Рис. 4. Типичная квазиустойчивая конфигурация КА с тремя состояниями клетки: I (ингибитор) - чёрный круг, А (активатор) - белый и S (основание) - точка
В процессе исследования диффузии на. ГС [9] авторами были получены аналоги глай-деров игры «Жизнь». На рис. 4 изображена, пушка, периодически испускающая глайдеры. Этот КА начал свое развитие в случайной начальной конфигурации (с 1/3 вероятностью каждой клетки). Можно видеть, что есть два. типа, стационарных локализаций: глайдеры-пожиратели и спиральная глайдер-пушка, которая испускает шесть потоков с частотой один глайдер в шесть шагов по времени. Пожиратели обычно уничтожают глайдеры, сталкивающиеся с их центром, а также могут изменить тех, которые взаимодействуют с внешним краем.
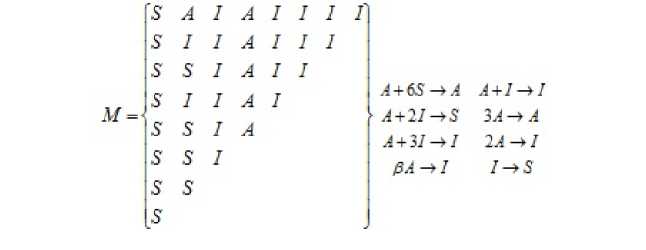
Рис. 5. Правила перехода для КА через матрицу (слева) и квазихимическими реакциями (справа)
Правила перехода задаются матрицей М = (mij ), где 0 6 г 6 7, 0 6 j 6 7, и mij G {I, А, S } (рис. 5). Индекс г задается количеством соседей, состояние которых I, индекс j - соседей с состоянием А. Индекс для состояния S не нужен, так как его можно получить как 7 — (г + j ). Новое состояние может быть представлено формулой
Xt+1 = M§2(;c)t5i(;c)t , где 5р(х) - число соседей элемента х с состоянием р G {I, А, S}.
КА на ГС также используются при моделировании процессов кристаллизации. На рис. 6 представлена последовательность картин скелетного роста кристалла в разные моменты времени, полученная в работе Э. Абашевой [10]. Моделью с дополнительными условиями фазового перехода описывается рост кристалла хлористого аммония NH4CI.
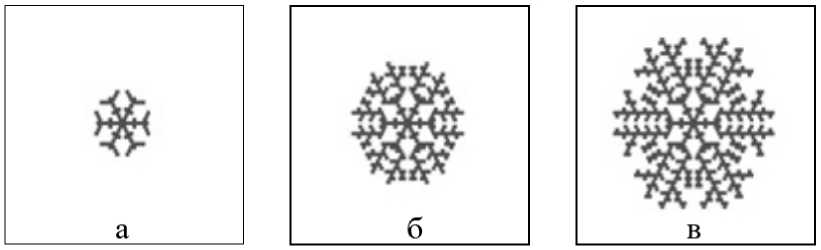
Рис. 6. Снежинкоподобные формы роста кристалла в разные моменты времени: a) t = 10; б) t = 18; в) t = 25
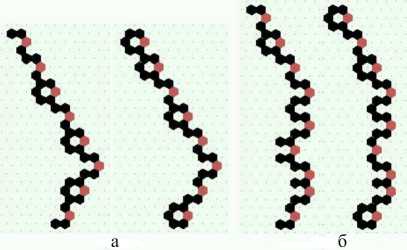
Рис. 7. Полимероподобные глайдеры с периодом 2. Движение цепочки слева направо (показаны 2 последовательных хода/состояния). Правила перехода задаются kcode = = 0022000220022001122200021210
Построение различных нуклеиновых цепочек рассматривается у Эндрю Вуенша [11].
Глайдеры движутся слева направо с периодичностью 1, 2 и 4. На рис. 7 показаны 2 ви- да полимерно-подобных глайдеров с периодом 2. Каждая клетка может находиться в 3-х состояниях, различающихся по цвету (2 - чёрная клетка, 1 - красная, 0 - точка).
С помощью таких паттернов, на наш взгляд, можно моделировать термически активированное движение атомных ступенек вещества по поверхности твердого тела [12] или дать семантическую интерпретацию движения олигомерных пептидов при электрофорезе.
Тоталистинные КА на планарной ГС
КА называется тоталистичним, если его локальная функция перехода зависит только от суммы состояний соседей и, быть может, состояния центральной ячейки. Тогда локальная функция перехода легко шифруется [11] числом kcode. Для КА размерности (г, к), где г - число состояний, к - количество соседей одной клетки (соседство), существует £ = ((щу—Дгу возможных переходов для каждой клетки. Составив таблицу всех возможностей соседства для каждой клетки и задав правило перехода для неё, мы получим kcode. Например, для КА размерности (3,6) (рис. 6) для одного правила число возможных переходов L = 28 (табл. 1).
Таблица!
Правила перехода, задаваемых kcode = 0022000220022001122200021210
|
Состояние 0 |
Состояние 1 |
Состояние 2 |
Новое состояние |
|
|
0 |
6 |
0 |
0 |
0 |
|
1 |
5 |
1 |
0 |
1 |
|
2 |
4 |
2 |
0 |
2 |
|
3 |
3 |
3 |
0 |
1 |
|
4 |
2 |
4 |
0 |
2 |
|
5 |
1 |
5 |
0 |
0 |
|
6 |
0 |
6 |
0 |
0 |
|
7 |
5 |
0 |
1 |
0 |
|
8 |
4 |
1 |
1 |
2 |
|
9 |
3 |
2 |
1 |
2 |
|
10 |
2 |
3 |
1 |
2 |
|
11 |
1 |
4 |
1 |
1 |
|
12 |
0 |
5 |
1 |
1 |
|
13 |
4 |
0 |
2 |
0 |
|
14 |
3 |
1 |
2 |
0 |
|
15 |
2 |
2 |
2 |
2 |
|
16 |
1 |
3 |
2 |
2 |
|
17 |
0 |
4 |
2 |
0 |
|
18 |
3 |
0 |
3 |
0 |
|
19 |
2 |
1 |
3 |
2 |
|
20 |
1 |
2 |
3 |
2 |
|
21 |
0 |
3 |
3 |
0 |
|
22 |
2 |
0 |
4 |
0 |
|
23 |
1 |
1 |
4 |
0 |
|
24 |
0 |
2 |
4 |
2 |
|
25 |
2 |
0 |
5 |
2 |
|
26 |
1 |
1 |
5 |
0 |
|
27 |
0 |
0 |
6 |
0 |
Рассмотрим, например, строчку 16. Если клетка имеет 2 соседа в состоянии 2, 3 соседа в состоянии 1 и 1-го соседа в состоянии 0, то она переходит в новое состояние 2. Заметим, что kcode записывается в обратном порядке из цифр последнего столбца.
КА на ГС можно использовать для исследования простых процессов репликации [13]. Напомним алгоритм для 2-х состояний КА Фредкина (0 и 1) - переход в другое состояние происходит по следующим правилам: для каждого элемента находится сумма состояний соседей, новое состояние остаётся прежним, если эта сумма чётная, и меняется на противоположное, если нечетная: ^сос/е=01010101010101010/10101010101010101 (kcode представлен дробью, т.к. центральная ячейка входит в собственную окрестность).
Наше исследование проводилось средствами оригинальной программы SoftCAM [14]. Для начала рассмотрим аналоги игры «Жизнь» на ГС для двух состояний (0 и 1). На рис. 8 и рис. 9 представлено несколько паттернов с периодом 2. Здесь мы не учитываем вклад центральной клетки в общие правила перехода.
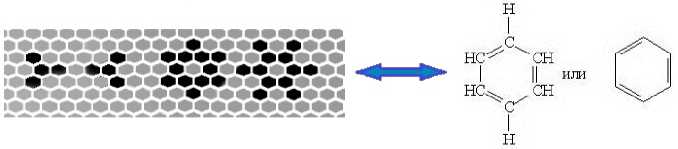
Рис. 8. Симметричные изомероподобные паттерны в ГС-аналоге КА Конвэя
•***••*•**••**•**•**

Рис. 9. Несимметричные изомероподобиые паттерны в ГС-апалоге КА Конвэя
Можно увидеть, что происходит некоторое «вращение», а именно перебежка крайних точек по кругу. Паттерн на рис. 8 подобен типу связи в молекуле СбНб, в которой sp2-связь постоянно меняет своих соседей. Хотя на уровне химической связи такая аналогия непродуктивна ввиду наличия более совершенных квантово-химических программ моделирования, тем не менее она представляется уместной (см. рис. 9) при моделировании динамических состояний атомно-кластерных структур, самоорганизующихся на поверхностях.
Для удобства введем некоторое обозначение. Пусть запись [а, Ь] для КА на ГС, по типу игры Конвэя, обозначает следующее правило:
-
1) клетка при сумме состояний её шести соседей, меньшей а и большей Ь, переходит в состояние 0 («умирает»);
-
2) при сумме, равной а или Ь, переходит в состояние 1 («рождается»);
-
3) в остальных случаях не меняет состояние.
КА рис. 8-9 работает по правилу [3, 4]. В таком семействе автоматов интересны правила [2, 2], [2, 3], [3, 3.. .6], т. к. здесь можно наблюдать устойчивые паттерны. В остальных же случаях вычислительные эксперименты показывают либо неограниченный рост (иногда симметричный), либо полное вымирание.
Влияние граничных условий. Влияние реконфигурируемого шаблона
«Игровые» КА обычно разыгрываются на бесконечной доске, но моделирующие нано-размерные процессы КА обычно требуют задания граничных условий. Можно выделить три типа последних: а) «линия смерти»; б) замыкание; в) изолированность. В первом случае все граничные клетки всегда имеют состояние 0. Во втором случае для граничных ячеек шаблон окрестности продолжается за счет ячеек на «другом конце Вселенной». Например, прямоугольная сетка превращается де-факто в свернутый цилиндр. Для ГС условие замыкания возможно лишь при ограничениях на четность числа столбцов и строк. В третьем случае за счет формального исключения из шаблона граничной ячейки соседей работа локальных правил перехода может быть либо скорректирована, либо оставаться прежней. Несомненно, что следует из опыта решения задач математической физики, условия на границах также могут повлиять на развитие КА. Фактор замкнутости играет важную роль для КА в наноэлектронике, в отличие от «игровых» КА.
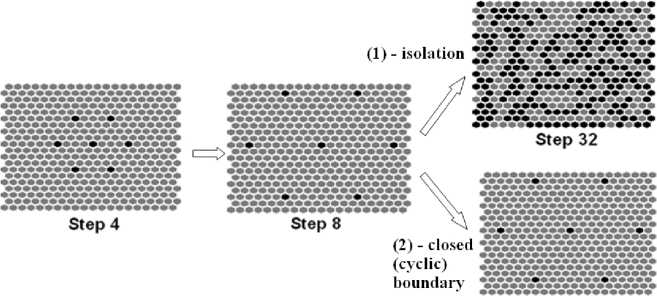
Рис. 10. Влияние условий на границах на поведение КА. Пример для правил Фредкина
Рассмотрим битовый КА Фредкина на ГС и с начальной конфигурации в 1 живую клетку. На рис. 10 представлены два варианта развития КА на ГС 20 х20 для случая изолированного и замкнутого циклически поля при одинаковых начальных условиях. При замыкании наблюдается характерная для КА Фредкина (на квадратной сетке) периодичность, причём размер ГС был 2m х 2m (m > 1), а начальные условия допускали вариабельность.
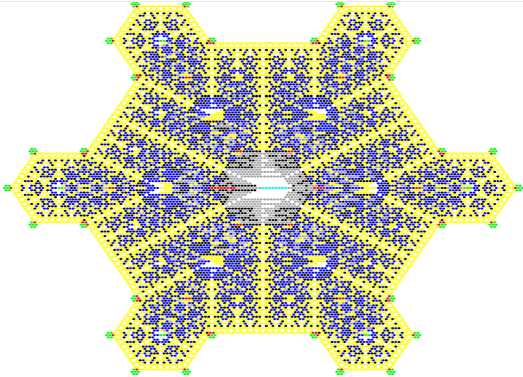
Рис. 11. Антисимметричный КА на ГС («ласточка»). Использовались модифицированные правила Фредкина для 8 цветов
КА на ГС тяготеют к симметричным фигурам с тремя осями симметрии. Потеря центральной симметрии в фигуре «ласточка», полученной нами случайно из-за ошибок в коде, приведших к появлению пространственно реконфигурируемого шаблона (рис. 11). Эта «ошибка», заключающаяся в присоединении к 6 ячейкам стандартного гексагонального шаблона двух ячеек справа или слева (в зависимости от четности ряда), свидетельствует о глубинной взаимосвязи прямоугольной и гексагональной сеток.
Подробнее о правилах в этом КА. Каждая ячейка может быть в одном из 8 состояний (0, 1, 2, 3, 4, 5, 6, 7), в данном случае каждому состоянию соответствует свой цвет. Начальной конфигурацией является правильный шестиугольник, составленный из семи ячеек сетки в состоянии 7 и фона в состоянии 0. Правила перехода задаются подобно алгоритму Фредкина - при чётном числе соседей состояние ячейки не меняется, а при нечетном - состояние изменяется на следующее по кругу. Но принципиальным отличием является то, что для четных рядов учитываются только соседи слева, а для нечетных только соседи справа.
Семантика КА на ГС с двумя состояниями
Для некоторых тоталистичных КА на ГС с двумя состояниями были обнаружены устойчивые унарно- и/или бинарно-периодические структуры - агломераты (рис. 12), состоящие из чередований в близком к шахматному порядку ячеек 0-го и 1-го состояния. К сожалению, рисунок не может вполне передать динамику изменения состояния поля КА. Возможная семантическая интерпретация: хаотический поток жидкости течет по поверхности между химически инертными островками, огибая их.

Рис. 12. Образование инертных агломератов шахматного порядка в бинарном КА с kcode = 0111100. Примерные границы одного из агломератов выделены зеленой линией
В большинстве случаев в правилах перехода мы учитывали только соседство текущей ячейки. Но можно также учитывать состояние и центральной клетки. Мы рассмотрели КА, реализующий аналог игры жизнь в зависимости от состояния центра. КА имеет два состояния 0 и 1, начальное расположение - случайное, правила задаются дробью [2, 6]/[3, 5] (рис. 13а, б). В этом КА наблюдается самоорганизация частиц в группы, очертания которых остаются четкими на протяжении некоторого количества ходов. Но со временем каждая группа разрастается и в конце концов разделение по группам исчезает.

Рис. 13. Самоорганизация в КА, зависящего от состояния центральной ячейки: а - шаг 0,6- шаг 100
Паттерны КА на ГС с тремя состояниями
Интереснее рассмотреть КА с 3-мя состояниями. Так, например, глобальная конфигурация одного из них (kcode=kbase, рис. 14) из начального рандомного состояния после некоторого числа ходов, рисунок характеризуется большим многообразием (например, в сравнении с классической игрой «Жизнь») глайдеров, т.е. прямолинейно движущихся паттернов. При встрече глайдеров друг с другом могут происходить: аннигиляция (взаимное уничтожение при столкновении), отсутствие взаимодействия (продолжение движения после столкновения) или несохранение импульса (изменение направления движения).
Количество всевозможных правил для тоталистичных КА формулы (и, к) равно ик, а в нашем случае 36 = 729 вариантов. Уменьшить количество рассматриваемых автоматов можно, зафиксировав некоторые строки в таблице 1. При этом можно избавиться от бесконечного роста или, наоборот, от полного вымирания. Так, например, зафиксировав следующие строки: kcode [19] = 1; kcode [20] = 2; kcode [23.. .27] = 01000 и сократив объем выборки, мы нашли глайдеры в КА с определенными правилами (табл. 2). Конечно, для других правил и способов фиксации kcode глайдеры также могут присутствовать. Здесь мы упираемся в ресурсные ограничения эксперимента.
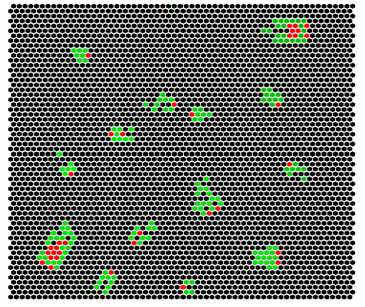
Рис. 14. Разнообразие глайдеров в КА на ГС, задаваемого kcode = = A;&ase=2200122221211110101122001000. В большинстве случаев направление движение глайдера задается его «головой», отмеченной одной или двумя красными точками
Таблица2
Некоторые правила наряду с kbase, порождающие глайдеры
0101002002210000101122201000;
1200122011001110101120001000;
0010122201010210211120001000;
1201010010210122110120001000;
0102222210111010210120001000;
2221010222010101000120101000;
2110122210011011000120001000;
2121211100222101000121101000;
1222010021201210201120001000;
Изменяя первоначальный kcode=kbase в одной позиции, можно «улучшить» правила. Так, паттерн «пожиратель» (по терминологии игры «Жизнь»), встретившийся в КА с правилом kcode = 2200122221411110101122001000, способен поглощать глайдеры при лобовом и/или касательном взаимодействии (рис. 15а, б). Жирным выделена позиция, которую мы изменили. В основном «пожиратель» сохраняет своё состояние, «восстанавливаясь» от удара в течение нескольких ходов. Ещё в этих правилах встречаются паттерны, обладающие свойством самовоспроизведения (рис. 15в).
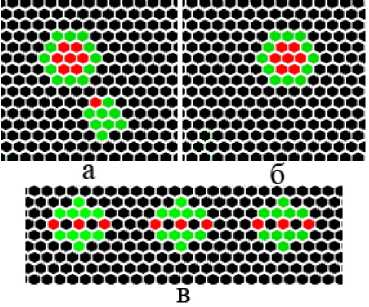
Рис. 15. Глайдер-пожиратель (а - до столкновения, б - после него) и паттерн, копирующий сам себя, kcode=kbase минус 1 в позиции 11
Заключение
В статье мы сделали краткий обзор по клеточным автоматам на гексагональной сетке, дали описание особенностей и методов задания шаблонов ГС, а также простейших КА на ГС. Нами были рассмотрены несколько существующих KA-моделей физико-химических процессов и способы записи правил локального перехода. В экспериментальной части была исследована зависимость поведения КА от граничных условий и реконфигурируемых шаблонов, в частности впервые получена ассиметричная фигура «ласточка». Так же мы исследовали простейшие тоталистичные КА на ГС с 2- и 3-мя состояниями, были найдены несколвко паттернов и глайдеров, для которых дана смысловая интерпретация в контексте нанотехнологий. В целом можно сделатв вывод, что в сравнении с квадратными сетками и окрестностями Неймана и Мура КА на ГС обладают большим многообразием паттернов, тяготеют к симметрии по шести направлениям, то есть обладают изотропностью, желательной для моделирования наноструктур.
Список литературы Особенности гексагональных клеточных автоматов на плоской поверхности для задач нанотехнологии
- Ванаг В.К. Исследование пространственно распределенных динамических систем методами вероятностного клеточного автомата//УФН. -1999. -Т. 169, № 5. -С. 481-505
- Медведев Ю.Г. Метод моделирования трехмерных потоков жидкости клеточными автоматами//Автометрия. -Т. 41, № 3. -2005. -С. 37-48
- Афанасьев И.В. Исследование эволюции клеточных автоматов, моделирующих процесс «разделения фаз» на треугольной сетке//Прикладная дискретная математика. -2010. -Т 10, вып. 4. -С. 79-90
- Бандман О.Л. Клеточно-автоматный метод исследования свойств пористых сред//Сибирский журнал вычислительной математики. -2010. -Т. 13, № 1. -С. 1-13
- Коноваленко И.С., Смолин А.Ю., Псахье С.Г. Многоуровневое моделирование деформации и разрушения хрупких пористых материалов на основе метода подвижных клеточных автоматов//Физическая мезомеханика. -2009. -Т. 12, № 5. -С. 29-36
- Лиманова Н.И., Мамзин Е.А. Высокопроизводительные клеточные автоматы с реконфигурируемым шаблоном//Вектор науки ТГУ. -№ 1(15). -2011. -С. 28-30
- Наумов Л.А. Метод введения обобщенных координат и инструментальное средство для автоматизации проектирования программного обеспечения вычислительных экспериментов с использованием клеточных автоматов: дис. на соиск. уч. ст. канд. техн. наук/СПбГУ ИТМО. -2007. -283 с
- Мамзин Е.А. Высокопроизводительные клеточные автоматы с реконфигурируемым шаблоном и их применение для моделирования неоднородных динамических систем: автореф. дис. канд. физ.-мат. наук/Тольяттин. гос. ун-т. -2011. -20 с
- Adamatzky A., Wuensche A. Computing in spiral rule reaction-diffusion hexagonal cellular automaton//Complex Systems. -2006. -№ 16. -С. 277-297
- Абашева Э.Р. Исследование и моделирование процессов кристаллизации с применением клеточных автоматов: автореферат дис. канд. техн. наук/Рос. хим.-технол. ун-т им. Д. И. Менделеева, Москва. -2007. -22 с
- Wuensche A. Glider dynamics in 3-value hexagonal cellular automata: the beehive rule -Discrete Dynamics Lab and Faculty of Computing, Engineering and Mathematical Sciences, University of the West of England. -2005. -24 p
- Асеев А.Л.,Латышев А.В. Электронная и ионная литография: наноструктурирование (приглашенный доклад)//IV Всероссийская конференция «Физические и физико-химические основы ионной имплантации», Новосибирск, 23-26 октября 2012
- Samira E.Y., Bastien C., Stefania B. Cellular Automata//7th International Conference on Cellular Automata, for Research and Industry, Perpignan. -2006
- Матюшкин И.В., Хамухин А.В. Применение языка UML при проектировании клеточных автоматов//Известия вузов. Электроника. -2010. -№ 6. -С. 39-48


