Особенности геометрического моделирования утраченных памятников архитектуры

Актуальность изучения архитектурного наследия очевидна. Без этой работы невозможны реставрация и реконструкция как отдельных памятников, так и архитектурных комплексов, невозможна реабилитация исторически сложившейся архитектурно-природной среды. В настоящее время востребованными становятся методики, позволяющие проводить архитектурный анализ, направленный на моделирование и оценку исторической застройки [1].

Геометрическое моделирование утраченных сооружений по фотографиям представляет собой процесс реконструкции их облика. Определяются форма и размеры памятника архитектуры в целом, а также отдельных его деталей, то есть реконструируется геометрическая модель. Под геометрическим моделированием утраченных памятников архитектуры подразумевается процесс создания геометрической модели существовавшего в прошлом сооружения на основе различных источников информации.

Предпочтительной геометрической моделью утраченного памятника архитектуры является масштабный чертеж или трехмерная модель сооружения, но при недостатке исходной информации это может быть и безмасштабный чертеж или аксонометрическое изображение. Источниками информации для моделирования служат результаты полевых, библиографических или архивных изысканий, закономерности, выявленные при изучении приемов и канонов возведения аналогичных сооружений. Практически вся информация, используемая при моделировании, нуждается в критическом анализе, так как неясности выражения в тексте, нечеткости изображений, противоречивость различных источников придают ей вид случайных величин, подчиненных нормальному закону распределения ошибок. Даже авторский чертеж может быть недостоверным, так как часто серьезные изменения в облик сооружения вносились после разработки проекта в процессе строительства. То есть ни один источник информации в отдельности не позволяет достигнуть качественного моделирования сооружения.

С точки зрения количества геометрической информации важнейшим ее источником являются иконографические материалы (архивные фотографии, литографии, рисунки и т. д.). Из них наиболее информационно емки и максимально объективны фотографические изображения (объективность может быть снижена при ретушировании), а также обмерные чертежи остатков объекта. Точность и достоверность информации зависят от вида и состояния фотографии, от особенностей съемочного оборудования. Например, негатив или репродукция, сделанная контактным способом, содержат более качественную информацию, чем репродукции, выполненные с помощью фотоувеличительного оборудования или литографией с применением ретуширования. Искажение прямолинейности на фотографии зависит от устройства объектива фотографического аппарата.

Моделирование утраченных памятников архитектуры по иконографическим материалам – это процесс, состоящий из трех этапов, каждый из которых является элементарной единицей системы этого процесса и привносит важные промежуточные результаты, составляющие при совместном чтении по определенным правилам конечный продукт – модель объекта [4].

Первый этап – сбор информации и представление ее в стандартном виде . Он состоит из натурных и архивных исследований. Натурные исследования представляют собой составление обмерного чертежа сохранившейся части сооружения или его следов и обследование подобных памятников архитектуры с целью выявления особенностей конструкции. Архивные исследования – это поиск иконографических и текстовых материалов. Собранную информацию надо обработать, привести к удобному для использования на следующих этапах реконструкции виду. На фотоматериале надо опознать те элементы (точки, прямые, отрезки прямых и т. д.), размеры или положение которых в пространстве известно из других источников. Например, линии карнизов, окон, конька крыши горизонтальны и параллельны между собой, углы здания вертикальны и их положение определено на плане по чертежу остатков фундамента. Требуется привести к единой системе измерения всю собранную информацию о размерах, перевести все старинные меры измерения в современные, оценить ошибку каждого размера.

Второй этап – метризация проекционной модели. Модель может быть одномерной (прямолинейный ряд точек), двухмерной (плоское поле точек), трехмерной (точки в трехмерном пространстве). Метризация (определение абсолюта и масштаба [13]) возможна, если известно достаточное количество информации. Каждый опознанный на фотографии элемент обладает определенным количеством информации (параметров) [15], которое измеряется числом связей, наложенных на элемент в пространстве, минус единица. Например, прямая, у которой в пространстве известно только направление (две связи) – один параметр, точка в пространстве (три связи) – два параметра. Набор данных, достаточный для метризации изображения, будем называть репером [13].

Вопросы метризации исследовались многими авторами, по этой теме имеется обширная литература, в которой рассматриваются отдельные виды изображений [1] и реперов [13].

В зависимости от вида метризуемого изображения требуется различное количество параметров. Например, трехмерная задача, аксонометрическое изображение – пять параметров, центральная проекция – шесть параметров, растянутая по одному из направлений центральная проекция (анаморфная центральная проекция) – восемь параметров [15]. Существует бесчисленное множество видов реперов [7], на основе которых можно смоделировать проекционный аппарат. Сам процесс моделирования возможен различными путями, например по специальному алгоритму или методом итерации.

Третий этап – моделирование объекта . В зависимости от того, какая решается задача (одномерная, двухмерная, трехмерная), применяется соответствующий алгоритм. Действия на этом этапе основаны на теории решения метрических задач [3], [5].

Достоверность модели утраченного памятника архитектуры измеряется величиной ошибок линейных и угловых размеров. Факторы, отрицательно влияющие на ее величину, делятся на три группы. Первая группа факторов – ошибки, вызванные тем, что такие геометрические понятия, как прямолинейность, перпендикулярность, параллельность и т. д., применяемые при моделировании, не существуют на реальных объектах. Практически невозможно построить здание абсолютно правильной геометрической формы. Технические средства и приемы работы мастеров прошлого не обеспечивали точную обработку материалов, полную повторяемость формы одинаковых деталей. Снижение влияния первой группы отрицательных факторов при моделировании возможно на основе глубокого изучения аналогичных сооружений, приемов работы. Следствием этого являются правильный выбор вида репера, а также обеспечение его избыточности. Если репер вместо шести требуемых параметров будет содержать семь или более параметров, то элементы проекционного аппарата можно определить шесть или более раз, а затем усреднить результаты.

Вторая группа неблагоприятных факторов – ошибки исходных данных. Они обусловлены ценой деления применяемых инструментов, сохранностью сооружения, степенью четко- сти контуров постройки на фотоснимке или его литографической репродукции, величиной случайных наложений, закрывающих здание на фотоснимке. Пути снижения ошибок данной группы вытекают из их природы. Это применение более точных инструментов, повышение резкости фотоснимков с помощью специальных приемов и технологий, а также использование избыточной информации в виде нескольких фотографий, позволяющей определять положение элементов сооружения несколько раз, производить проверку и усреднение результатов.

Третья группа факторов – это ошибки, возникающие в процессе вычислений и построений. Они обусловлены методами округления промежуточных результатов, количеством операций, а также способом вычисления (графический или аналитический). Влияние этих факторов можно уменьшить, совершенствуя алгоритм вычисления или построения.

Повысить точность конечного результата моделирования можно, во-первых, традиционным путем: инструментально-технологическими способами и совершенствованием алгоритма. Существуют и нетрадиционные пути: 1) представление информации, с одной стороны, как случайных величин, подчиненных нормальному закону распределения ошибок, с другой стороны, как нечетких множеств; 2) использование для построений и вычислений избыточной информации [8]. Первый предполагает замену идеальных геометрических элементов и понятий на нечеткие, вероятностные. Так, точка представляется эллиптической областью, центр которой является ее номинальным положением, а границей – заданная ошибка, описываемая нормальным законом распределения [10]. Прямая – это область, ограниченная ветвями гиперболы. Номинальное положение прямой – мнимая ось гиперболы [9]. Любой геометрический элемент представлен нечеткой областью. Пересечение нечетких элементов есть нечеткий элемент. Например, пересечение двух нечетких прямых – это нечеткая точка.

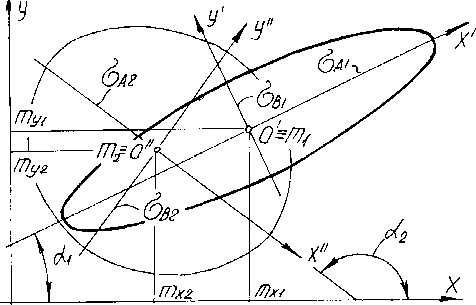
Мера принадлежности двух собственных нечетких точек на плоскости (рис. 1) есть величина:

I ( T ₁ ² T ₂ ² ) = max{ µ _T 2 ( m ₂), µ _T 2 ( m ₁)} ,         (1)

где µ _T 2 ( ^u 1^{, u} 2 ) – функция принадлежности нечеткому множеству T ²; ^ T 2 ( u_Y, u ₂ ) - функция принадлежности нечеткому множеству T ₂ ² .

Две нечеткие точки на плоскости назовем принадлежными, если I ( T ₁ ² , T ₂ ² ) ≥ 0,5, и непри-надлежными, если I ( T ₁ ² , T ₂ ² ) <  0,5.

Формула для подсчета принадлежности двух точек [7]:

• _- i - i ²

• I ( T ₁ ² , T ₂ ² ) = max{ e ^{2 σ 2 A 1 σ B 21} , e ^{2 σ A 22 σ B 22} } ,         (2)

где I - расстояние между математическими ожиданиями нечетких точек.

О

Рис. 1. Определение меры принадлежности пары двухмерных нечетких точек: m – математическое ожидание; σ – среднее квадратичное отклонение

Геометрия, применяемая для действий с такими объектами, является модификацией проективной геометрии, учитывающей вероятностные свойства экспериментальной геометрической информации и нечеткий характер множеств. Причина применения проективной геометрии объясняется тем, что проективное пространство [15] (евклидово пространство с присоединенными к нему несобственными – бесконечно удаленными элементами) пригодно для исследования центральных проекций, которыми являются фотографии.

Второй путь – использование избыточной информации – заключается в том, что исследователь не выбирает оптимальный алгоритм, а использует все или, по крайней мере, множество алгоритмов построения и вычисления. В итоге получаем множество результатов, которые обрабатываются методами математической статистики с учетом неравноточных измерений [14]. Применение подобных методов описано в работе [12]. Отличие предлагаемой модификации геометрии заключается в более полном учете влияния погрешности на конечный результат (учитывается неравноточность результатов опытов). Поясним данное утверждение на примере определения точки схода вертикальных прямых на фотографии. Точка схода определяется множество раз как пересечение пар прямых. Каждая прямая представляет собой область, ограниченную ветвями гиперболы, где она может находиться с заданной вероятностью. Мнимая ось гиперболы проходит через центры эллиптических областей, представляющих точки Т11, Т12 и Т21, Т22 (рис. 2). Точкой пересечения пары прямых является точка-область Т, где эта точка пересечения может появиться с заданной вероятностью (рис. 2). Результаты построения точки схода (точки-области) обрабатываются методами математической статистики (рис. 3).

На основе теории неравноточных измерений разработана методика решения задач геометрического моделирования утраченных ар-

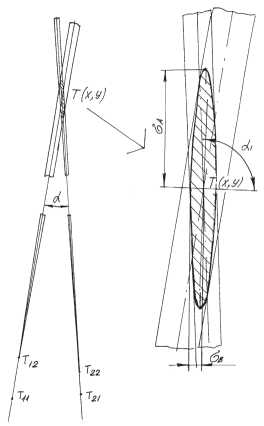
Рис. 2. Область возможных пересечений двух прямых. Т – точка пересечения пары прямых (точка-область); Т₁₁, Т₁₂, Т₂₁, Т₂₂ – точки (эллиптические области), через которые проходят нечеткие прямые; σ – среднее квадратичное отклонение

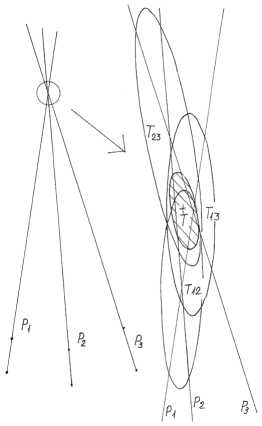
Рис. 3. Определение точки схода вертикальных прямых.

Р1, Р2, Р3– нечеткие прямые; Т12 – область возможных пересечений прямых Р1, Р2; Т13– область возможных пересечений прямых Р1, Р3; Т23 – область возможных пересечений прямых Р2, Р3; Т– область возможных пересечений прямых Р1, Р2, Р3

хитектурных объектов по иконографическим материалам, основанная на статистической обработке результатов с применением нечеткой проективной геометрии, созданной на основе теории нечетких множеств [7]. Создан комплекс программ, реализующих операции построений в нечеткой проективной геометрии и статистическую обработку результатов построения и предназначенный для решения практических задач геометрического моделирования утраченных памятников архитектуры.

Описанные методы использованы в ряде работ для геометрического моделирования утраченных и частично утраченных памятников архитектуры: часовня XVIII века в поселке Калевала (Ухта), церковь Иоанна Предтечи в селе Шуя, церковь Варлаама Хутынского в селе Рыбрека [6], церкви Ко-невской Богоматери и Ильи Пророка Валаамского монастыря, церковь Казанской Божьей Матери в деревне Росляково, Никольская церковь в селе Ладва, Сретенская церковь в поселке Соломенное, погост в селе Задняя Дуброва Архангельской области.

* Работа выполнена при поддержке Программы стратегического развития ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012–2016 гг.

CHARACTERISTIC FEATURES OF GEOMETRIC MODELING OF LOST ARCHITECTURAL MONUMENTS