Особенности использования конечно-объемного, дискретно-ординатного и диффузионного приближения для уравнения радиационного теплопереноса

Моделирование процесса радиационного теплообмена является очень сложной и ресурсоемкой задачей, так как в этом случае в отличие от остальных процессов теп-ломассопереноса каждый элементарный объем среды находится в непосредственном взаимодействии со всеми другими элементарными объемами и решение интегрально-дифференциальных уравнений, описывающих данное явление, очень трудоемко. Размерность уравнения, описывающего радиационный теплоперенос, может достигать шести измерений: три пространственных координаты х, у, z, две угловых координаты описывающие направление распространения излучения, и частота излучения.

Проблема выбора модели радиационного теплопереноса для расчета прикладных задач заключается в поиске баланса между временем счета и точностью, так как временные затраты на решение только уравнения радиационного теплопереноса (УРТ)

—^-^ = -P(r)/(r,s) + K(r)/4(r) +

могут существенно превосходить затраты на решение всех остальных процессов. Здесь/-интенсивность, Вт/(ср • м²); I - интенсивность абсолютно черного тела; ст - коэ<|)-фициент рассеивания,^¹; к -коэффициентпоглощения,^¹; Р - коэффициент затухания (Р = к + ст), м ; Q - телесный угол, рад; г - радиус-вектор, м; s - угловое направление, м; Ф - функция рассеивания.

Краткий обзор методов решения уравнения радиационного теплопереноса. Ниже будут рассмотрены три подхода к решению (1): диффузионное (Р1) приближение, конечно-объемный метод (КОМ), дискретно-ординатный метод (ДОМ).

Для решения прикладных задач с радиационным теп-лопереносом наиболее распространено использование Р1 -приближения. Оно основывается на предположении от изотропности поля излучения. Основные его плюсы -это простота и относительно малые затраты времени на одну итерацию. Ограничение, накладываемое на применение этого метода, вытекает из предположения, лежащего в его основе, сравнительно слабая анизотропия поля излучения [1].

Методы ДОМ и КОМ являются лучевыми. Они не имеют ограничений по применению, их точность зависит прежде всего от дискретизации углового пространства, однако временные затраты на одну итерацию могут быть существенно выше Р1-приближения. Отличие КОМ от ДОМ заключается в том, что при переходе к разностному аналогу (1), в ДОМ происходит интегрирование только по объему:

г Г ,dl‘ ^dl‘   tdI*A ц—+ъ—+п— W = dx dy dz )               (2)

= J (-p/z + Sr'yiVdM а в КОМ - еще и по угловому пространству [2]:

J J-- d¥dQ = J J (-p/'+^jjKJQ, ди'ДГ ds         ди'дг

S1 (гД) = к(г)1ь(г,$) +

где м, x, h - направляющие косинусы; /-1-е угловое на правление для ДОМ или 1-й дискретный телесный угол для КОМ.

Сравнение диффузионного приближения КОМ и ДОМ при решении различных задач. Область применения диффузионного приближения - это оптически толстые среды. Примером такой задачи может служить моделирование газовой топки.

Как правило, в газовых котлах критерий Буггера »1 и Р1-приближение достаточно хорошо описывает распределение поля излучения. Но в данной статье приведен пример нештатной работы котла, когда через две горелки поступает только воздух без топлива. Эго способствует возникновению сильного градиента температуры в области расположения данных горелок. Моделирование проводилось на основе программы «sFlow», разработанной совместно сотрудниками Красноярского филиала Институт теплофизики Сибирского отделения Российской академии наук, ООО «ТОРИНС» и Сибирского федерального университета. Использование методов Р1, КОМ и ДОМ для решения (1) приводит к формированию отличной друг от друга структуры поля течения (рис. 1). Так, Р1 и КОМ с 8 направлениями имеют структуру поля температур, отличную от остальных (рис. 1). При использовании ДОМ с направлениями поле температур выглядит схожим с полем ДОМ с 24 направлениями и КОМ с 3 2 направлениями, но применение в ДОМ такой малой дискретизации приводит к большой ошибке по тепловым потокам на стенках топки (табл. 1).

Таким образом, использование Р1 -приближения в оптически толстых средах дает малое отклонение по тепловому потоку от лучевых методов (в данном случае ~3 %). но может привести формированию другой структуры поля течения. Что касается лучевых методов, то использование малой угловой дискретизации в этом случае приводит к существенным ошибкам по тепловым потокам на стенки топки для ДОМ и по распределению поля температур для КОМ. поэтому для лучевых методов целесообразнее использовать большее число направлений.

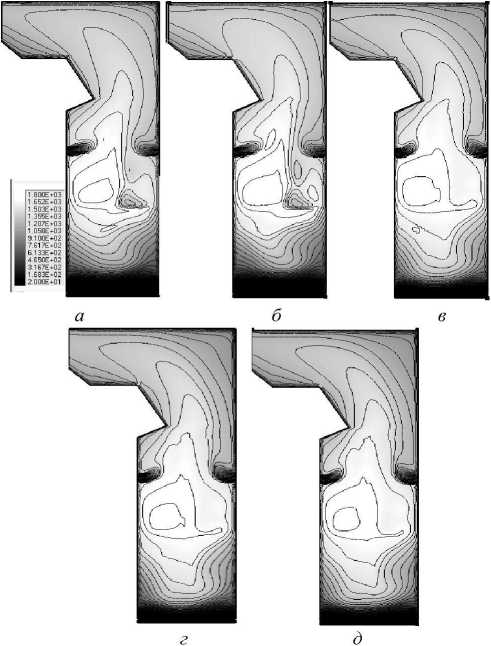
Рис. 1. Распределение поля радиационной температуры в котле (шкала 20-1 800 °C): а - Р1; б - КОМ (8 направлений); в - ДОМ (8 направлений); г - КОМ (32 направления); д - ДОМ (24 направления)

При снижении критерия Буггера меньше единицы в Р1-приближении, не только падает точность расчета, но и существенно возрастает количество итераций, требующихся для сходимости решения. Это может привести к тому, что основным критерием окончания расчета будет сходимость радиационной задачи, что в целом увеличивает время решения всей задачи радиационного теплопереноса.

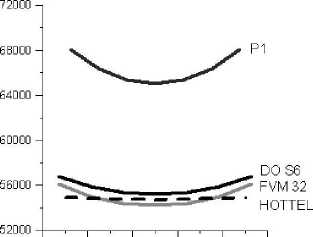
В работе [3]. где рассмотрено решение для идеализированной печи (рис. 2). критерий Буггера равен 0.8. Результаты расчетов сравнивались с эталонным решением задачи методом Хоттеля. Ошибка по температуре для Р1

от эталонного решения составила порядка 1 %, но по тепловым потокам на стенку - уже около 13 %. Лучевые же методы показали решение, очень близкое к эталонному.

Т=1200 К, е = 0.85

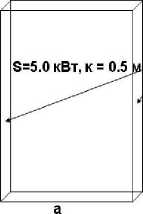
Т=900 К, = 0.7

b = 4.0 м а = 2.0 м

Т=400 К, е = 0.7

а

0      0.4     0 6      1.2      1.6      2

б

Рис. 2. Идеализированная печь: а - постановка задачи; б - тепловой поток с горячей стенки для разных методов решения УРТ: Р1-приближения: ДОМ с 48 дискретными направлениями ДО S6; FVM32 - КОМ с 32 дискретными направлениям; HOTTEL - эталонного решения зональным методом [4]

Лучевые методы по сравнению с диффузионным приближением сходятся быстрее, особенно в оптически тонких средах, но время, требуемое ими на одну итерацию возрастает примерно в п раз. где п - число угловых направлений. Сократить временные затраты можно путем замораживания радиационных источниковых членов в уравнении энергии в течение нескольких итераций.

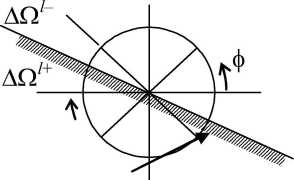
Один из недостатков тучевых методов (в большей степени КОМ) связан с их использованием для геометрически сложных объектов. В этом случае может наблюдаться угловое перекрытие, т. е. пересечение грани контрольного объема и дискретного телесного угла (рис. 3). и при недостаточном угловом разбиении в сильноанизотропных средах возникает серьезная ошибка. Для разрешения этой проблемы в КОМ можно использовать дополнительное разбиение телесного угла на два угла плоскостью грани. пересекающей телесный угол.

Таблица 1

Сравнение методов по температуре и величине теплового потока на стенки котла

Метод решения уравнения радиационного теплопереноса	Величина тепловой потока, Вт/м2
КОМ (8 направлений)	1,32Е + 08
КОМ (32 направления)	1,30Е + 08
Р1	1,26Е + 08
ДОМ (8 направлений)	1.551-08
ДОМ (24 направления)	1,29Е + 08

Представим расчет поля радиационной температуры в цилиндре радиусом 0,5 м и высотой 4 м, к = 0,1 м¹ (рис. 4), стенки которого имеют различные температуру и степень черноты. При малом количестве угловых направлений наблюдается сильный дисбаланс по энергии, если не учитывать угловое разбиение (табл. 2). В этой задаче среда является оптически тонкой и Р1 -приближение показывает сильное расхождение с лучевыми методами.

Грань контрольного объема

Рис. 3. Угловое перекрытие

Рис. 4. Сравнение методов на сетке с неортогональными ячейками (для Р1 шкала 600...630 °C, для лучевых -500...670 °C): а-сетка; б-Р1-приближение; в-ДОМ (48 направлений); г - КОМ (8 направлений с учетом углового перекрытия); д - КОМ (288 направлений без учета углового перекрытия)

Использование угловой многоблочности в КОМ. Конечно-объемный метод обладает дополнительным инструментом, позволяющим сократить время расчета. Этот инструмент-угловая многоблочность [4], когда различные расчетные области задачи могут иметь различную угловую дискретизацию (рис. 5).

Такой подход позволяет сокращать время расчета, если примерно известны оптические свойства среды. Приведем пример использования угловой многоблочности (рис. 6). Расчетная область имеет кубическую форму. Среда принимается неизлучающей, т. е. к = 0. Во всей области х < 0,5 м коэффициент рассеивания s принимается равным 2 м1, в остальной - равным нулю. На нижней стенке задается поток излучения q. Остальные стенки считаются абсолютно черными и неизлучающими. Размерность пространственной сетки составляет 22 х 22 х 22 узла.

Рис. 5. Схематическое отображение угловой многоблочности

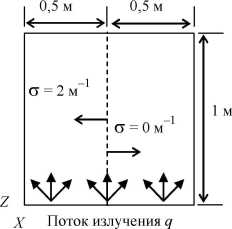
Рис. 6. Использование угловой многоблочности

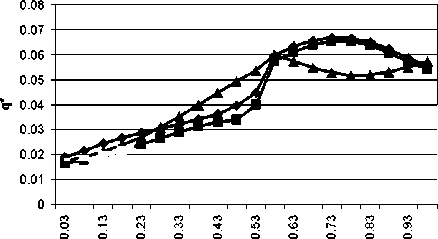
Представим результаты расчетов трех вариантов (рис. 7): первый вариант -288 телесных углов, второй - 32 телесных угла, третий -32 телесных угла в области о = 2 м1и 288 телесных углов, в области о = 0 м1. При использовании малого количества угловых разбиений (2-й вариант) наблюдался нефизичный провал. Для получения точного решения было существенно увеличено разбиение углового пространства (1-й вариант). Это привело к существенному росту времени счета (табл. 3). Использование угловой многоблочности (3-й вариант) позволило получить решение, достаточно близкое к 1-му варианту, при этом общее время счета уменьшилось в три раза. Возросло только количество итераций, что связано с дополнительной обработкой границы угловых блоков.

Интенсивный рост производительности вычислительных систем делает использование лучевых методов доступным для решения прикладных задач, но в геометрически сложных объектах в условиях сильной анизотропии излучения требуется достаточно сильная дискретизация этих методов по угловому пространству, что может привести к серьезному увеличению ресурсоемкости задачи. Диффузионное приближение в области прикладного моделирования до сих пор остается более привлекательным по соотношению времени счета к точности ре-

Таблица2

Пример влияния углового перекрытия

Угловое разбиение (кол-во углов) Потери энергии за счет схемы (Епад - Еисх / Еисх), % КОМ без учета углового перекрытия КОМ с учетом углового перекрытия ДОМ 8 207 12 ОО 24 57 5 77 48 10 — 4 288 4 — — шения. однако его использование в оптически тонких средах и при наличии сильных градиентов поля температуры приводит, к существенным ошибкам по распределению поля излучения и радиационным потокам на поверхности исследуемого объекта.

♦ 1-ый вариант * 2-ой вариант—■—3-ой вариант

Рис. 7. Распределение падающего теплового потока вдоль линии z = 1 м,у = 0,5 м