Особенности использования метода Монте-Карло в качестве метода оценки инвестиционного проекта

Оценка инвестиционных проектов на сегодняшний день является важным аспектом хозяйственной деятельности предприятия. Оценка эффективности проекта дает возможность не только оценить возможность его прибыльности и, как следствие, реализации, но в первую очередь определяет эффективность вкладываемых инвестиций, следовательно, формирует требования к источнику используемых инвестиций, за счет возможности варьирования срока возврата, за счет определения максимально допустимой процентной ставки и определения уровня риска рассматриваемого проекта.

Проблема оценки эффективности инвестиционных проектов не является новой, в то же время возникает все больше подходов к определению параметров проекта и прогнозирования зависимости результатов от заложенных параметров.

Таким образом, на сегодняшний день экономико-математическое моделирование является важной составляющей оценки инвестиционных проектов, так как позволяет проанализировать стохастические параметры проекта и уровень воздействия внешней среды.1

Важным разделом моделирования поведения проекта в условиях изменяющейся экономики является метод Монте-Карло. Данный метод основан на статистическом исследовании повторяемости проекта за счет математической его реализации в режиме реального времени. Для данных случаев используется программное обеспечение.

Так в качестве базы можно использовать ППП Excel, Project Expert, C++ и прочие программные среды.2 Как правило выбор программной среды для исследования проекта зависит от множества факторов, в первую очередь от возможностей исследования и целей. Предварительная оценка может быть дана на основании классического метода с использование небольшого числа итераций.

Рассмотрим метод Монте-Карло. Наиболее часто данный метод применяется для оценки риска проекта. Так как данная характеристика хуже всего поддается прогнозированию.

При оценке любого инвестиционного возникает необходимость оценки показателей эффективности, таких как чистая приведенная стоимость, внутренняя норма доходности, а также рентабельности инвестиций.

Данные показатели являются детерминированными, так как их расчетная величина четко определяется заложенными параметрами проекта, такими как объем инвестиций, денежные потоки по проекту, ставка дисконтирования. Для данных характеристик стохастическими (случайными) как правило являются величина спроса, определяющая денежные потоки, ставка дисконтирования, определяемая требуемой доходностью и параметрами риска проекта.

В рамках метода Монте-Карло анализ риска выполняется с помощью моделей возможных результатов. При создании таких моделей любой фактор, которому свойственна неопределенность, заменяется диапазоном значений - распределением вероятностей. Затем выполняются многократные расчеты результатов, причем каждый раз используется другой набор случайных значений функций вероятности. Порой для завершения моделирования бывает необходимо произвести тысячи и даже десятки тысяч перерасчетов - в зависимости от количества неопределенностей и установленных для них диапазонов. Моделирование по методу Монте-Карло позволяет получить распределения значений возможных последствий.

При использовании распределений вероятностей переменные могут иметь разные вероятности наступления разных последствий. Распределения вероятностей представляют собой гораздо более реалистичный способ описания неопределенности переменных в процессе анализа риска.

Для реализации неопределенности используется один из законов распределения вероятности, при этом желательно учитывать форму распределения, для более достоверного прогнозирования результатов.

Так, например, величина спроса на товары, как правило, подчиняется экспоненциальному закону распределения, если речь не идет о товарах первой необходимости, большинство макроэкономических параметров подчиняется нормальному закону распределения при условии отсутствия регулирования в условиях кризиса, то есть при регулировании на основании естественных факторов равновесия экономики.

Для практической реализации воспользуемся надстройкой Excel.

Рассмотрим проект инвестиций в облигацию предприятия, торгуемую на финансовом рынке. Текущая рыночная стоимость облигации составляет 8000 руб., при этом данная облигация предполагает выплаты в течение четырехлетнего периода по тысяче рублей в год, с погашением номинальной стоимости в конце четвертого года в размере 10000 руб. Для определения уровня доходности необходимо задать уровень инфляции. По прогнозным данным он составит по годам 10%, 20%, 25% и 17%. Таким образом, текущая приведенная стоимость составит:

^PV 1 + 0,1 ⁺ (1 + 0,1)(1 + 0,2) ⁺ (1 + 0,1)(1 + 0,2)(1 + 0,25)

1000 + 10000

+ (1 + 0,1)(1 + 0,2)(1 + 0,25)(1 + 0,17)   11944,13 руб'

Если рассматривать покупку данной облигации как инвестиционный

проект, то чистая приведенная стоимость по данному проекту составит:

NPV = -8000 + 11944,13 = 3944,33 руб.

С точки зрения подхода к инвестированию данный проект эффективен, но так как оценка уровня инфляции является прогнозной, то фактическая доходность может существенно отличаться. Именно поэтому в данном случае необходимо применение метода Монте-Карло.

Зададим параметры инфляции в виде усредненной ставки в пределах заданных параметров. То есть найдем среднее значение и среднеквадратическое отклонение оценки уровня инфляции.

купонная доходность Номинал Рыночная стоимость	1000 10000 8000	уровень инфляции		0,25	0,17
		0,2	0,1
Характеристики спроса
Среднее значение	0,18
Стандартное отклонение	0,062716

Рисунок 1 – Исходные данные по проекту

Расчет характеристик инфляции проводим на основании введенных исходных данных.

Среднее значение по формуле =СРЗНАЧ(E2:E5)

Стандартное отклонение по формуле =СТАНДОТКЛОН.В(E2:E4)

Так как в данном случае рассматривается такой макроэкономический параметр как инфляция, то полагаем, что он подчиняется нормальному закону распределения.

Дальнейший анализ проводим с учетом данного закона.

Размер случайного уровня инфляции определяется на основании встроенной функции =fmc_Normal(B6;B7).

Введя параметры случайной инфляции, получим расчетные данные.

После проведения 1000 испытаний, были получены следующие данные (рис. 2 и рис. 3). Однако метод Монте-Карло предполагает насколько вариантов моделирования.

Поэтому вторым способом предложен анализ на основании возможных значений процентной ставки с точностью до 1%.

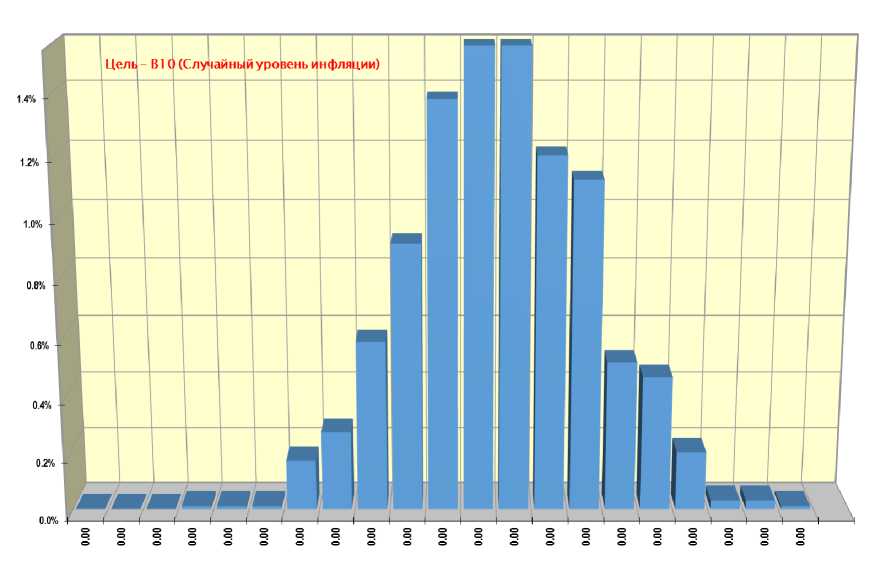
Рисунок 2 – моделирование уровня инфляции

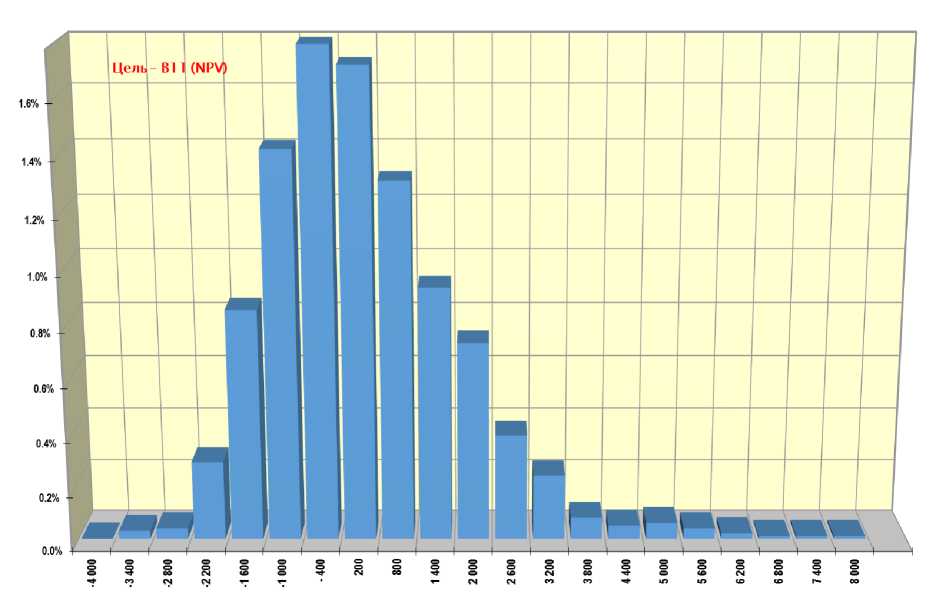
Рисунок 3 – Сумма NPV при заданном уровне инфляции методом

Монте-Карло (частотные распределения)

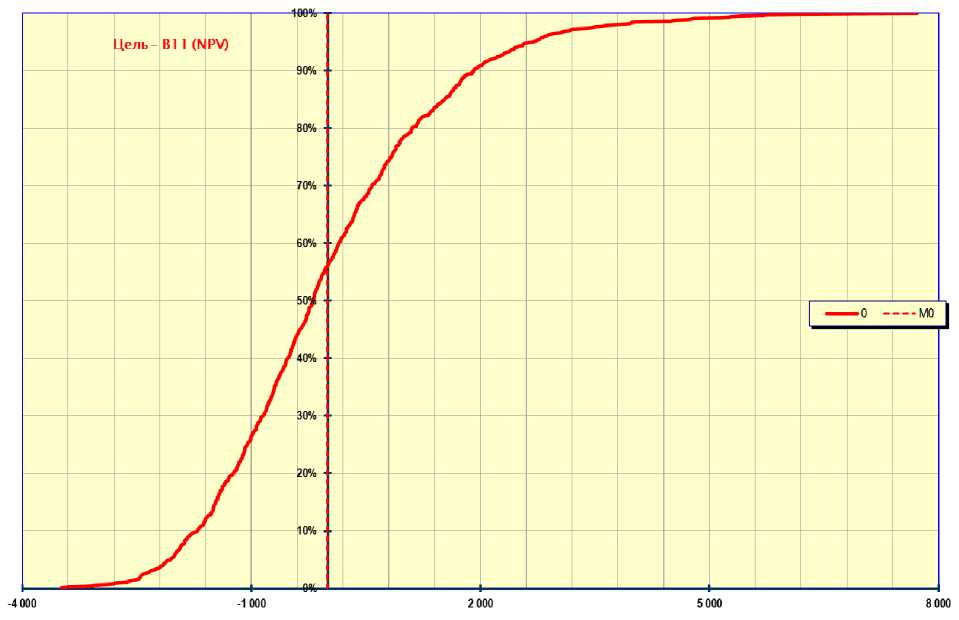
Рисунок 4 – Взаимосвязь ставки и уровня NPV

Для более детального анализа увеличим объемы вычислений и представим данные в численном выражении.

Накопленная статистика =         1 тыс.

Метод Монте-Карло.                  Время счета =    9,13 сек.

Целевая ячейка - B10 (Случайный уровень инфляции)

Значение

параметра

B10 ( Случайный уровень инфляции )

ее значение

отклонение

Станд.

отклонение

оценки

среднего

0,1 0,100

0,11

0,110

0,12

0,120

0,13

0,130

0,14

0,140

0,15

0,150

0,16

0,160

0,17

0,170

0,18

0,180

0,19

0,190

0,2

0,200

0,21

0,210

0,22

0,220

0,23

0,230

0,24

0,240

0,25

0,250

0,26

0,260

1,067E-08

1,725E-08

0,000E00

1,542E-08

2,050E-08

0,000E00

3,646E-08

2,843E-08

0,000E00

2,807E-08

2,134E-08

0,000E00

3,450E-08

4,904E-08

0,000E00

0,000E00

3,085E-08

значения

3,373E-10

5,454E-10

0,000E00

4,878E-10

6,483E-10

0,000E00

1,153E-09

8,989E-10

0,000E00

8,875E-10

6,747E-10

0,000E00

1,091E-09

1,551E-09

0,000E00

0,000E00

9,755E-10

Максимум

0,10

0,11

0,12

0,13

0,14

0,15

0,16

0,17

0,18

0,19

0,20

0,21

0,22

0,23

0,24

0,25

0,26

Минимум

0,10

0,11

0,12

0,13

0,14

0,15

0,16

0,17

0,18

0,19

0,20

0,21

0,22

0,23

0,24

0,25

0,26

Рисунок 5 – Численные результаты моделирования процентной ставки при заданных уровнях.

При втором варианте моделирования уровень инфляции определен на основании равномерного закона, что в некоторой степени противоречит стандартным экономическим законам, но в то же время допустимо в периоды кризисов и финансово-кредитной политики направленной на снижение темпов инфляции.

В данном случае очевидно, что модель имеет меньшую вариативность, но качество прогноза будет низким.

Третьим вариантом создадим набор показателей инфляции на основании нормального закона, но далее воспользуемся классической оптимизацией.

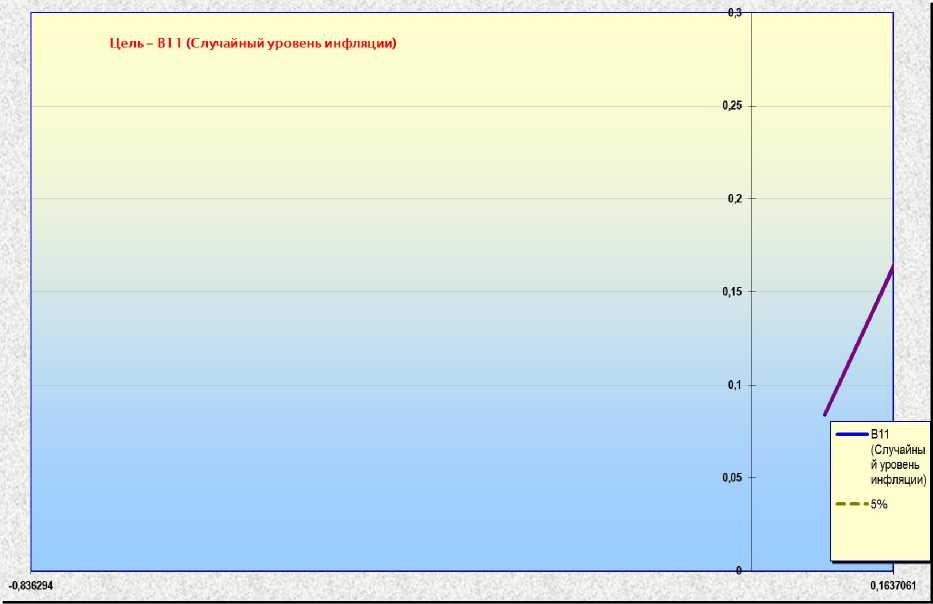
Рисунок 6 - Прогнозирование случайного уровня инфляции на основании экспоненциального закона

В заключительном случае результаты получены еще менее вариативные, но среднее значение определено с большей определенностью, так как меньше величина среднеквадратического отклонения.

Таким образом, на основании моделирования случайного уровня инфляции на основании введенных исходных данных отметим, что данный проект прибылен лишь при среднем уровне инфляции, составляющем 18%.

При этом необходимо также оценивать уровень рыночных продаж и доходность требуемую инвестором.3

В целом метод Монте-Карло позволяет провести оценку уровня риска проекта. В нашем случае проект выгоден, допускает реализацию. Так как фактический уровень инфляции, согласно опубликованным данным, в России планируется на 2017 год лишь на уровне 5%.

Итак, в результате исследования выявлено, что метод Монте-Карло используется для уточнения стохастической составляющей при исследовании эффективности инвестиционных проектов. Метод построен на многократном повторении и расчете средневыборочных значений.

Качество полученных результатов во многом зависит от правильности выбора закона распределения.

В целом данный метод дает уточненные показатели для инвестиционного проекта.