ОСОБЕННОСТИ ИСПОЛЬЗОВАНИЯ NIST ТЕСТОВ ДЛЯ АНАЛИЗА БИТОВЫХ СЛОЕВ ПОКРЫВАЮЩИХ ОБЪЕКТОВ В СИСТЕМАХ СТЕГАНОГРАФИИ

Стеганографические системы решают задачу маскировки скрываемых сообщений открыто передаваемым покрывающим объектом. Для выявления скрытых сообщений используют стеганографический анализ. Существует два основных подхода к обнаружению скрытых сообщений – визуальный (наличие искажений, артефактов и пр.) и статистический. Визуальная оценка является малоэффективной и имеет ограниченную область применения, так как не позволяет обрабатывать большие объемы пересылаемых данных. Поэтому, задача стеганографического анализа сводится к статистическому анализу потоков информации. Результатом статистического анализа является предположение о наличии или отсутствии скрытого сообщения.

При разработке стеганографической системы мы имеем исходный покрывающий объект и объект с встроенным сообщением. Это позволяет оценить вносимые в покрывающий объект искажения. При стеганографическом анализе произвольного потока информации есть только исследуемый объект [1], представляющий собой битовую последовательность. Это снижает достоверность выводов о наличии скрытых сообщений.

Таким образом, исследование статистических характеристик битовых последовательностей представляет собой важнейшую задачу при разработке стеганографических систем и стеганографическом анализе.

Важно, что в зависимости от типа объекта (изображение, звук, файл данных и др.) битовые последовательности имеют свои особенности, определяемые статистическими характеристиками объектов, наличием сжатия и пр., что обязывает стегоаналитика тщательно подходить к разработке средств стеганографического анализа и адаптировать их под конкретные информационные объекты с целью поиска аномалий в битовых последовательностях. Особенно это актуально при разработке новых стеганографических систем, которые должны быть обоснованно лучше, а инструментария для обоснования этого, как правило, не хватает.

Достаточно распространенным инструментом для анализа битовых последовательностей является дивергенция Кульбака-Лейблера, позволяющая оценить отличия распределений значений [1–3]. В работах [3; 4] для решения задачи оценки распределений значений используется коэффициент корреляции Пирсона, который удобен тем, что принимает значения в диапазоне от -1 до 1, что упрощает сравнение результатов различных экспериментов. Заметим, что оценка распределения значений показывает лишь количество нулей и единиц и дает крайне ограниченное представление о статистических свойствах битовых последовательностей. В ряде работ встречаются и другие статистические оценки, например, критерий χ2 Пирсона [1], тест Маурера [5] или статистические тесты на основе функции ошибок [6].

Увеличение количества и разнообразия используемых для стеганографического анализа статистических тестов позволяет повысить достоверность выводов о наличии скрытых сообщений.

В работах [7; 8] для стеганографического анализа привлекались NIST тесты, содержащие развитый статистический аппарат. Данные тесты являются стандартом США и используются для анализа битовых последовательностей достаточно большой длинны (как правило, от 1 млн. бит) и содержит 15 тестов. NIST тесты построены таким образом, что по итогу их проведения делается вывод о «случайности» или «не случайности» битовой последовательности. При этом во всех тестах используется показатель P-value («tail probability»), принимающий значение в диапазоне от 0 до 1. Если значение меньше, чем 0,01, то последовательность считается неслучайной.

Недостатком предложенной в работах [7–9] технологии является использование тестов в их прямом виде. Иными словами, в указанных работах сравнение битовых последовательностей заключалось в оценке, какие тесты пройдены, или не пройдены анализируемыми битовыми последовательностями. То есть, результат работы NIST тестов представлялся в виде 15 битовых значений. Сравнение разных битовых рядов большой длины сводилось к сравнению разных 15 битовых рядов, являющихся результатом тестирования. Пример тестирования из диссертационной работы Нгуен Н.К. приведен на рисунке 1 [9]. При этом отбрасывается большой объем значений больше 0,001.

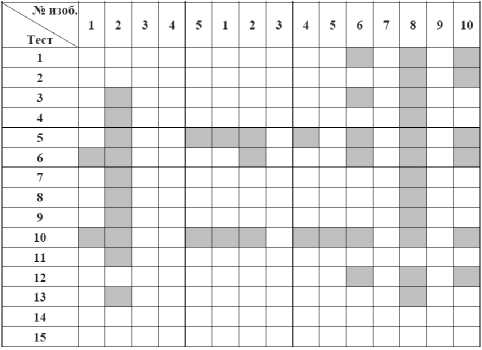
Рисунок 1. Результаты NIST-тестирования для 15 различных покрывающих изображений. Серый цвет указывает, что тест пройден

Анализ тестов, описанных в стандарте [10] показал, что, при правильном подходе, они могут дать большее количество информации об объекте.

Математический аппарат тестов определен, однако проведение самих тестов дает определенную гибкость. Для одних тестов это размер исследуемого блока, для других размер и количество анализируемых подблоков или набор искомых битовых «образцов».

В работе предлагается развитие идеи использования NIST тестов с целью анализа статистических свойств покрывающих объектов за счет использования большего объема информации, который они дают.

Моделирование NIST тестов

Для лучшего понимания технологии NIST тестов авторами был разработан программный продукт на языке Python в соответствии со стандартом [10]. Следует отметить, что некоторые тесты позволяют получить более одного результата для битовой последовательности. Общее количество полученных результатов тестирования в соответствии со стандартом и выбранными параметрами для каждого из тестов сведено в таблицу 1. Таким образом, общее количество результатов тестирования равно 114 значениям от нуля до единицы. Заметим, что в задачах стеганографии факт случайности или не случайности битовой последовательности носит условный характер, поскольку больший вес имеет сравнение битовых последовательностей и поиск взаимных зависимостей между битовыми последовательностями.

Таблица 1. Количество результатов по каждому из тестов

Номер теста	Название теста	Количество результатов
1	Frequency (monobit) test	1
2	Frequency Test within a Block	1
3	Runs Test	1
4	Test for the Longest Run of Ones in a Block	1
5	Binary Matrix Rank Test	1
6	Discrete Fourier Transform (Specral) Test	1
7	Non-overlapping Template Matching Test (8 бит)	74
8	Overlapping Template Matching Test	1
9	Maurer’s «Universal Statistical» Test	1
10	Linear Complexity Test	1
11	Serial Test	2
12	Approximate Entropy Test	1
13	Cumulative Sums (Cusum) Test	2
14	Random Excursions Test	8
15	Random Excursions Variant Test	18

По этой причине мы отбросили уровень 0,01, определяющий случайность битовой последовательности в пользу получения набора значений P-value статистических характеристик битовой последовательности.

В рекомендациях к NIST тестам [10] указано, что рекомендуемая длина битовой последовательности должна составлять от 106 значений для полу- чения адекватного вывода о случайности последовательности. В поставленной задаче этим условием можно в некоторой степени пренебречь, так как нас интересует сравнение битовых последовательностей по набору статистических характеристик.

Дело в том, что битовые слои (изображения, звука) зачастую не являются абсолютно случайными величинами. Поэтому, чем длиннее битовая последовательность, тем больше вероятность, что она не пройдет тест на случайность, что приведет к получению результата теста, близкого к нулю в большей части тестов. Это не позволит отследить статистические зависимости битовых последовательностей. Помимо этого, работа тестов занимает достаточно продолжительное время. Так для обработки 106 точек может потребоваться до 20 минут времени (в зависимости от производительности вычислительной системы), что соответствует лишь малой части современных покрывающих объектов.

В экспериментах длина битовых последовательностей выбиралась в диапазоне от 100 000 до 500 000 значений. Эксперименты на изображениях и звуковых файлах показали, что в данном диапазоне статистические результаты слабо зависят от длинны битовой последовательности.

Анализ случайных битовых последовательностей

Для демонстрации технологии тестирования покажем результаты анализа различных битовых последовательностей с помощью полученных программ реализации тестов.

Первый эксперимент проведем со встроенным в Python генератором случайных чисел. Исследуем последовательности разной длинны. Первая последовательность имеет 106 отсчетов, а вторая – 105 отсчетов. Причем вторая последовательность является частью основной. Это позволит оценить влияние длины последовательности на полученные результаты. Представление результатов в виде таблицы ненаглядно, поэтому сформируем столбцовую диаграмму полученных значений (рисунок 2).

Видно, что последние 18 тестов дают практически идентичный результат, в то время как остальные тесты дают значительно отличные друг от друга результаты. Заметим, что, если бы стояла задача определения случайности, то мы бы получили практически одинаковый результат.

Сравним теперь различные последовательности одинаковой длинны, сгенерированные одним генератором (рисунок 3).

Видно, что разброс значений значителен во всем диапазоне, за исключением проваленного 14 теста. По проведении первогоэксперимента уже можно увидеть, что количество информации, содержащейся на рисунках 2 и 3 гораздо больше, нежели на рисунке 1. Более того, сравнение последовательностей из 15 бит, приведенных на рисунке 1 крайне ограничено, в то время, как статистическое сравнение приведенных на рисунках 2 и 3 отсчетов предоставляет широкие возможности по выявлению взаимосвязей.

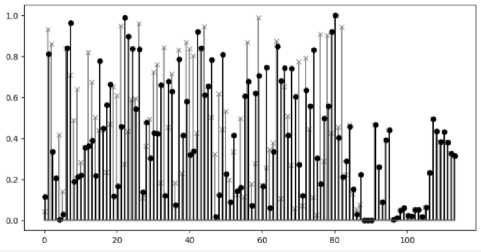
Рисунок 2. Результаты анализа битовых последовательностей разной длинны: 105 точек – маркер «x», 106 точек – маркер «o»

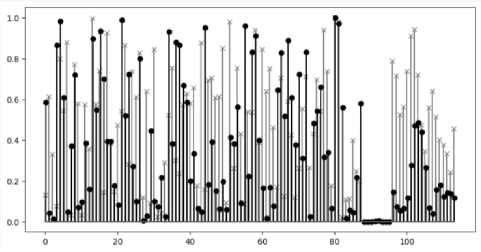
Рисунок 3. Результаты анализа битовых последовательностей одинаковой длинны

Проведем эксперимент с анализом битовых слоев изображений. Воспользуемся фото в формате bmp, с цветовой палитрой «оттенки серого», приведенном на рисунке 4.

Рисунок 4. Тестовое изображение «Долгоносик»

Проведем исследование двух младших битовых слоев тестового изображения. Для этого преобразуем квадратный массив в одномерный и передадим полученный массив в программу, реализующую тесты. На рисунке 5 приведены ре- зультаты тестирования.

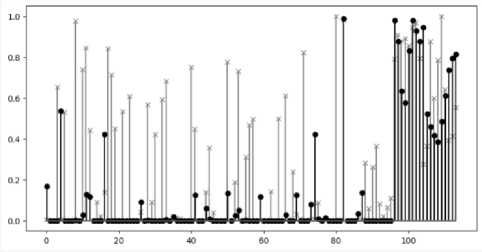
Рисунок 5. Результаты анализа битовых слоев: восьмой (младший) битовый слой – маркер «x», седьмой битовый слой – маркер «o»

Видно, что результаты сильно отличаются друг от друга и от результатов для битовых последовательностей генератора псевдо-случайных чисел.

Разберем отличия детально. Для этого вернемся к условию, что последовательность можно считать случайной в соответствии с конкретным тестом, если результат теста больше чем 0,01. То есть, чем выше значение, тем меньше проявляет себя статистическая зависимость между битами последовательности. На рисунках 2 и 3 можно увидеть, что значительная часть отсчетов больше заданного уровня 0,01, что говорит о характере последовательности, близком к случайному. На рисунке 5, младший битовый слой (маркеры «х») проходит ряд тестов на случайность, однако, заметно, что количество «проваленных тестов» гораздо больше, нежели у генератора псевдо-случайных чисел. Это очень важное наблюдение, так как существует мнение, что младший битовый слой фотографий соответствует белому шуму. Данное утверждение подкрепляется физикой процесса фотографирования (младший бит находится на пределе чувствительности сенсоров), визуальным представлением и распределением значений битов. Таким образом, данный эксперимент показал, что распространенное мнение о случайности младшего битового слоя справедливо только частично, и с помощью предлагаемого способа анализа легко выявляется визуальное отличие данной битовой последовательности от битовой последовательности псевдо-случайных чисел. Иными словами, если в младший битовый слой поместить случайную последовательность битов, то с помощью предлагаемого анализа можно зафиксировать искажение изображения.

Седьмой слой (черный цвет и маркеры «о») уже явно отличается, так как «проваливает» значительное количество тестов. Таким образом, использование второго битового слоя изображения для встраивания скрываемой информации не рекомендуется, так как здесь характер распределения значений окажется менее случайным.

Для сравнения приведем результаты анализа двух старших битовых слоев – 0 и 1 (рисунок 6). Видно, что верхние битовые слои «проваливают» все тесты кроме последних двух, что говорит о неслучайном характере битовых последовательностей.

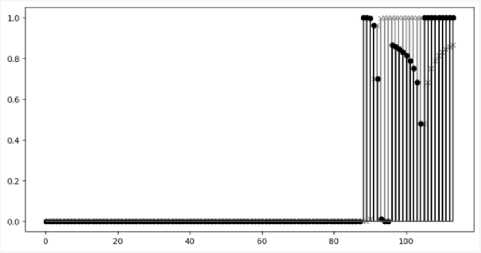
Рисунок 6. Результаты анализа битных слоев: нулевой (старший) битный слой – маркер «x», первый битный слой – маркер «o»

Приведем еще один пример. Теперь исследуем изображение RAW, полученное с матрицы фотоаппарата. На рисунке 7 приведен оригинал фотографии (преобразованный в bmp без сжатия).

Рисунок 7. Тестовое изображение «Город»

Для того, чтобы не выходить на большие длительности последовательностей, выберем фрагмент, размером 1000 на 1000 точек и разобьем его на три массива по каналам цветности. После чего выполним тестирование. Пример фрагмента (красный канал) приведен на рисунке 8.

Цель исследования – продемонстрировать результаты тестов для RAW изображения по цвето- вым каналам, а также проверить степень случайности битовых последовательностей в различных слоях изображения.

Рисунок 8. Красный канал фрагмента тестового изображения «Город»

На рисунке 9 приведен результат тестирования младших битовых слоев по каналам. Видно, что в двух каналах младшие битовые слои действительно близки к случайным последовательностям, в то время, как красный «проваливает» большое количество тестов.

слоя. Данное утверждение справедливо и для двух других цветовых каналов.

Полученные результаты уже будут сложнее для проведения визуального анализа. Однако есть ряд моментов, которые видны и без привлечения статистического инструментария. Если сравнить полученные результаты двух младших слоев красного канала (рисунки 9 и 10), то можно увидеть, что характер битовых последовательностей менее случаен, чем в других каналах. Причем тесты, пройденные младшим слоем частично совпадают с тестами пройденными вторым слоем. Таким образом можно сделать вывод о наличии статистической связи между битовыми слоями в пределах одного канала. Наличие такой связи может носить фундаментальный характер, так как сильное искажение одного из слоев может привести к пропаданию статистической связи между слоями, что заставляет сделать вывод о наличии аномалии в изображении. Кроме этого, даже при высоком количестве тестов, пройденных младшими битовыми слоями в зеленом канале (рисунок 9), количество проваленных тестов больше, чем у последовательности псевдо-случайных чисел. Таким образом, предлагаемый анализ позволяет увидеть значительное количество результатов тестирования и сформировать «статистический портрет» информационного объекта с целью исследования стеганографических систем [11].

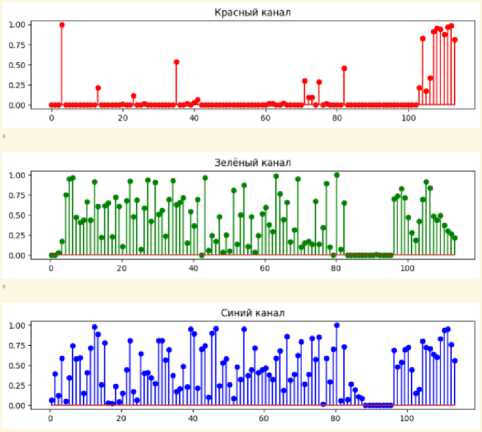
Рисунок 9. Результаты анализа младших битовых слоев

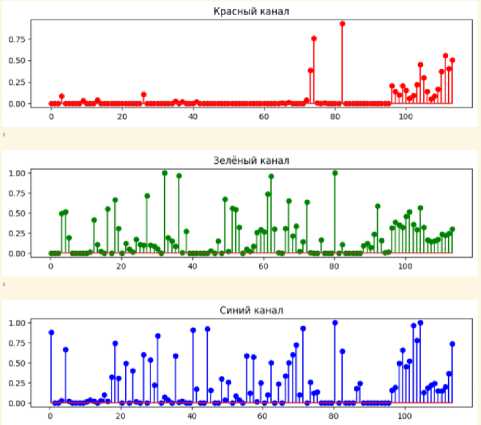
Рисунок 10. Результаты анализа седьмых битовых слоев

На рисунке 10 приведены результаты тестирования 7-го битового слоя (следующий после младшего). Видно, что красный канал менее случаен, по сравнению с другими каналами, при этом сохраняется и уменьшение «случайности», характерное для случая увеличении битового

Выводы

Проведенные исследования показали, что использование аппарата NIST тестов дает широкие возможности для статистического анализа битовых последовательностей при стеганографическом анализе.

Применение полного перечня результатов тестирования без упора на уровень 0,01, который определяет случайный характер последовательности, позволяет:

• 1.    Сформировать расширенное статистическое описание битовой последовательности.

• 2.    Провести статистическое сравнение двух и более битовых последовательностей и установить статистическую взаимосвязь. между последовательностями.

• 3.    Провести расширенный статистический анализ покрывающих объектов до встраивания сообщений, и стеганографических систем после встраивания сообщений.

• 4.    Использовать искуственный интеллект для принятия решения о наличии встроенной информации.

Решение указанных задач является важнейшим инструментом оценки MIDI объектов с точки зрения задач стеганографии и стеганографического анализа, в том числе и в вопросах оценки эффективности новых стеганографических методов.