Особенности итеративной регуляризации в обратных задачах рассеяния

Обратные задачи рассеяния формулируются следующим образом [1]: по заданной диаграмме направленности (ДН) определить или форму рассеивателя, или распределение поверхностного тока для идеально проводящего рассеивателя известной формы, или поверхностный импеданс рассеивателя. Очень близки по постановке к обратным задачам рассеяния методы восстановления амплитудно-фазового распределения (АФР) излучающих систем по результатам измерений в ближней зоне [2]. Этот класс задач относится к некорректно поставленным, что вызывает значительные трудности при решении практических задач антенной техники, радиолокации и радионавигации. При этом для произвольно заданной ДН или углового распределения эффективного поперечника рассеяния (ЭПР) решение обратной задачи существует не всегда, а если существует, то не зависит непрерывно от исходных данных [1]. Кроме того, для обратных задач характерна статистическая постановка, связанная с тем, что результаты практических измерений сопровождаются случайными погрешностями, вызванными соответствующими точностными характеристиками измерительной аппаратуры зондирования электромагнитных полей, неточным определением координат при позиционировании зонда. Это означает, что численные методы решения обратных задач должны сопровождаться статистическими оценками полученных результатов.

Рассмотрим следующую задачу: пусть известна форма идеально проводящего рассеивателя, заданная как поверхность S , удовлетворяющая условиям непрерывности Ляпунова – в любых точках p , q , принадлежащих S , существуют векторы нормалей n _p , n _q , для которых выполняется неравенство

I n p - n J <  c\p - q\ ^a , (1)

где c, 0 < a < 1 - произвольные числа. Будем считать, что на произвольной вспомогательной поверхности Sd задано множество точек с координатами (xn, yn, zn), n = 1: N, координаты точек определены со случайными ошибками (Axn, Ayn, Azn): (xn,yn, zn ) = (xn,yn, zn ) + (Axn, Ayn, Azn), где (xn, yn, zn) - точные координаты. В точках (xn, yn, zn) заданы АФР составляющих вектора напряженности электрического поля Exn, Eyn, Ezn , также определяемые со случайными ошибками: (Exn, Eyn, Ezn ) = (Exn, ЕУп , Ezen ) + (AExn, AEyn, AEzn ) , где (Exn, ЕУп ,Ezn ) - точное значение поля. Введем координаты точек на поверхности рассеивателя S: (x'n,y'n,z'„) = (x'ne,yne,z'ne') + + (Axn,Ayn,Azn), n = 1:N, где необходимо восстановить значения АФР поверхностного тока (jxn, Jyn, Jzn ). Составляющие поверхностного тока связаны с заданными составляющими вектора напряженности электрического поля строгими электродинамическими соотношениями следующего вида:

E x

E y

E z

с

= ^j j. 2 B r + ik s к

к

= —J — j ik S L

rr

r

D -

—

D + j_y 2 B_r +

к

iy^Dr — j^-- D ds '; -           -

- x^ D r

—

r

rvr.

j ID ds ';

-

Zc_j jxr iks

rr

—

j D + j_z 2 B r +

r

к

-X + -V D

-

ds ‘ ,

7 _

где k = 2 п(Х - волновое

число; Z c = ^ц a p aa - волновое сопротивление среды; s _a , ц _a

абсо-

лютные диэлектрическая и магнитная проницаемости среды; -_x = x — x '; -_y = y — y '; r_z = z — z ';

- = -Xr_x + - y 2 + -_z ² ; функции B_r

1 I ik 1 I                  1

—I —+—г I ф ; Dr = — 4п к - -2 7         4”

Г k k"

4 пк -

_ 3ik_I

-2

Ф ; ф = exp ( — ik- ) Jr .

Таким образом, задача восстановления АФР поверхностного тока по заданному АФР вектора напряженности электрического поля является типичной некорректной задачей, сформулированной в виде системы интегральных уравнений I рода. Строго говоря, система (2) относится к классу функциональных уравнений, так как области определения искомых и заданных функций не совпадают. Кроме того, численное исследование системы (2) затруднено влиянием случайных ошибок при определении функциональных зависимостей. Для формирования полной математической модели (ММ) рассматриваемой задачи необходим выбор метода дискретизации системы (2), приводящего к системе линейных алгебраических уравнений (СЛАУ). Этот метод должен учитывать еще одну специфическую особенность ММ, связанную с необходимостью использования квадратурных формул высокой точности, например, Гаусса-Лежандра с числом узлов не менее 16 и выше. Это требуется для обеспечения необходимой устойчивости численного решения, в значительной степени зависящей от случайных факторов задачи. Поэтому любое повышение точности вычислительных процедур в конечном итоге приводит к стабилизации математического моделирования. Без ограничения общности будем считать, что размерности множеств точек задания АФР (Exn, Eyn, Ezn) и определяемых АФР токов (jxn, jyn, jzn ) совпадают. Обсуждение вопросов построения ММ с недоопределенными или переопределенными СЛАУ выходит за рамки настоящей статьи. Широко используемый метод моментов для решения интегральных уравнений приводит к следующей формулировке ММ задачи восстановления (выбор базисных и весовых функций соответствуют методу коллокации):

N

Exn = У Лт^”П + j'vrnKmx' + ЛтК^П ; xn         xm xx ym yx zm zx m=1

N

E yn = 2 ( j xm K Xm.n + J, m Ky+ J rn K m;); m = 1

N mn       mn       mn

Ezn / ( jxmKxz' ⁺ jymKyz' ⁺ jzmKzz ' ) ^; n ^1: N , m = 1

где коэффициенты СЛАУ определяются численным интегрированием соответствующих функциональных зависимостей ядра системы уравнений (2) по поверхностям конечных элементов. Методы дискретизации поверхности S для построения оптимальной структуры конечных элементов рассмотрены в [3]. Необходимо отметить, что для трехмерных (3D) задач большой электрической размерности СЛАУ может иметь очень высокий порядок. В этом случае компьютерные ресурсы являются естественным ограничением возможностей математического моделирования обратных задач рассеяния в строгой электродинамической постановке. Для преодоления та- ких ограничений широко используются приближенные методы, основанные на асимптотических представлениях решений краевых задач электродинамики, например, методы физической оптики и геометрической оптики. Эти методы позволяют получить решение с приемлемой точностью только в рамках принятых допущений о геометрии и размерах рассеивателей, а также для ограниченных угловых областей.

Вместе с тем на практике достаточно часто встречаются задачи, в которых асимптотические представления полей излучения в дальней зоне для 3D рассеивателей соответствуют полям излучения в плоскости, перпендикулярной оси эквивалентных двумерных (2D) рассеивателей – случай E -поляризации [4]. Например, система вибраторных антенн вертикальной поляризации, расположенных вблизи протяженных цилиндрических объектов (антенны радио- и телевещания, базовых станций мобильной связи, установленные на мачтах и башнях). Тогда система (2) значительно упрощается и может быть представлена одним уравнением [5]. Будем считать, что ось z совпадает с продольной осью рассеивателей, тогда

E z ( x , y ) = - i. J Jz ( x ', y ‘ ) H 2 ( kr ) dl' , 4 _L

где L – контур, образованный сечением рассеивателей плоскостью, перпендикулярной их оси; r = ^ r 2 + r y ; H ₍2 ( kr ) - функция Ганкеля второго рода нулевого порядка. Численное решение уравнения (4) дает возможность прогнозировать поведение АФР токов для тех рассеивателей, влияние которых может приводить к искажениям поля излучения. Уменьшить такое влияние можно, например, изменением расположения антенной системы относительно рассеивателей. В частности, учет влияния поясов и опор башни (мачты) в общей структуре поля излучения антенной системы дает возможность синтеза АФР токов, формирующих ДН в наибольшей степени приближенной к заданной.

В идеализированной постановке, когда отсутствуют погрешности определения поля излучения, координат точек, в которых находятся АФР токов, численное решение уравнения (4) может быть получено как прямыми, так и итерационными методами, которые имеют свои особенности и области применения. Для задач большой размерности широкое применение получили итерационные методы, например, минимизации обобщенных невязок, сопряженных градиентов. Используемый программный комплекс MATLAB предоставляет разработчикам ММ широкие возможности для составления программ с использованием эффективного представления матричных форм Function Handle, а рациональная организация блочной структуры СЛАУ с использованием неявных вложенных циклов дает возможность значительно повысить быстродействие программ. Важным достоинством итерационных методов является возможность пошагового контроля скорости сходимости и нормы невязки решения. Кроме того, предварительные численные эксперименты для однотипных задач могут дать практический интервал значений нормы невязки, при которых достигаются как удовлетворительная точность решения, так и приемлемое время расчетов.

Значительно расширяет возможности математического моделирования обратных задач рассеяния использование суперкомпьютеров. Большое количество вычислительных экспериментов, проведенных на кластере «СКИФ-Урал» Южно-Уральского государственного университета, показывают, что полный цикл моделирования электродинамических задач, включающий в себя формирование СЛАУ размерностью порядка 1,3 - 10 9 элементов и решение прямым методом исключения Гаусса не превышает 3 минут. Использование итерационных методов решения СЛАУ позволяет увеличить размерность задачи в десятки раз, но при этом быстро нарастает время решения.

Особенностью уравнений (2), (4) является ярко выраженная неустойчивость численного решения, характерная для некорректных задач. Это можно подтвердить следующим численным экспериментом. Пусть контур L представляет собой окружность радиуса a, ka = 12. Идеально проводящий рассеиватель возбуждается плоской волной. На первом этапе будем считать, что все исходные данные определяются точно, то есть все погрешности отсутствуют. Численное решение ИУ (4) методом коллокации определяет АФР тока на контуре L , при этом точки на- блюдения и точки источников принадлежат L . С помощью этого тока в заданных точках вне L можно определить АФР поля рассеяния Ez . Будем считать, что это поле является исходным для решения обратной задачи рассеяния. В отсутствии погрешностей относительное изменение нормы токов прямой и обратной задачи не превышает величины 10-6, что позволяет считать эту задачу устойчивой. На втором этапе введем случайные изменения амплитуды и фазы заданного поля Ez . Без ограничения общности будем считать, что случайные изменения имеют равномерный закон распределения. С помощью генератора случайных чисел rand и процедуры масштабирования введем аддитивные случайные изменения амплитуды и фазы с относительной погрешностью 10-8. Норма тока в этом случае имеет порядок 106 относительно той же величины для устойчивой задачи. Если относительные случайные изменения значений поля имеют величину порядка 10-3, что характерно для большинства практических методов повышенной точности измерений в сверхвысокочастотном диапазоне, то норма восстановленного тока имеет порядок 1011 . Следовательно, рассматриваемая задача восстановления АФР тока может быть решена только с использованием методов регуляризации.

Широкое применение для решения некорректных задач получили итеративные методы регуляризации [6]. Для детализации постановки задачи запишем уравнение (4) в операторной форме:

Az = u , z е Z , u е U . (5)

Введем метрические пространства X , Y и отображение G : X ^ Y , заданное на подмножестве D g с Y . Требуется по элементу x е D g найти его образ G ( x ) е Y . В терминах операторного уравнения (5) G = A ^{- 1}, X = U , Y = Z и задача состоит в определении A ^{- 1}. В этом случае D g = AZ с U . Для корректной задачи отображение G определено на всех X и непрерывно. Если вместо элемента x е D g задано его неточное значение x 5 е X , то вводится норма разности элементов x ₅ , x в метрике X р _X ( x ₅ , x ) <5, где 5 - число, характеризующее погрешность задания x 5 . Будем требовать, чтобы численный метод решения уравнения (5) удовлетворял следующему основному требованию: чем точнее задано x 5 (чем меньше 5 ), тем точнее можно определить x . Основываясь на результатах работы [6], сформулируем регуляризирующий алгоритм следующим образом: определить оператор R , который ставит в соответствие паре ( x ₅ , 5 ) элемент z 5 е Z , причем z 5 ^ z в метрике Z при 5^ 0. Это означает, что R ( x 5 , 5 ) имеет смысл приближенного решения задачи при заданном наборе входных данных. Введем следующие итеративные схемы, отвечающие свойствам оператора R ( x ₅ , 5 ) [6]:

^z n + 1 = z n ^- ц ( A* Az n - A* u ) , z 0 = 0, ⁰ <ц< 2/ II A II; ⁽⁶⁾ (* 1 * 1 *

E + pA A) zn -(E + ^AA) Au, ц> 0, (7) где ц - параметр итеративной регуляризации; A * - оператор, сопряженный к A; E - единичный оператор. Как показано в [6], схема (6) применяется для ограниченного оператора A , а схема (7) – в случае неограниченного замкнутого оператора A . В частности, если A – интегральный оператор Фредгольма из W2l) (Q) и L2 (Q) (что соответствует рассматриваемой задаче), то использование схем (6) и (7) при l = 0,1, _ позволяет получить схемы регуляризации l = 0,1, _ порядков.

Итеративные регуляризирующие схемы должны быть дополнены правилами останова, предоставляющие широкие возможности для коррекции параметра ц в зависимости от скорости сходимости итерационного процесса и погрешности задания исходных данных. Правило останова регламентирует число итераций n ( 5 ) так, чтобы lim n ( 5 ) • 5 = 0.

Характерной особенностью схем (6) и (7) является отсутствие четких рекомендаций по выбору оптимального параметра ц . Большое количество вычислительных экспериментов численного решения задачи (4) с помощью схем (6), (7) позволяют предложить следующую методику определения оптимального параметра ц (необходимо отметить, что этот параметр в значительной степени зависит от величины 5 , поэтому эта методика не может считаться универсальной, но для задач с незначительно отличающейся геометрией и величинами 5 получаемые оценки ц могут быть использованы как стартовые для задач с другими входными значениями).

• 1.    Вводится серия параметров ц 1 , ц ₂ , ..., ц _k . Для рассматриваемой задачи восстановления АФР тока по неточно заданным значениям поля в некоторой области D эксперименты показывают, что эти значения могут находиться в интервале 10 3 ..4 ■ 10⁴.

• 2.    Для этой серии параметров ц последовательно применяется одна из итеративных схем для одинакового числа итераций m .

• 3.    Для каждого параметра ц из серии находится невязка квазирешения || z_m - z m _1|| .

• 4.    Из серии вычислительных экспериментов находится оптимальный параметр ц opt ^ min|| z_m - z m _11| , например, методом интерполяции кубическими сплайнами.

• 5.    Для ц _opt проводится полная прогонка итеративной регуляризирующей процедуры с введенным правилом останова, если до его выполнения не произошло прерывание процесса при условии достижения заданной точности восстановления ^z - — z _t _1||/ z _max < А .

Рассмотрим практическую реализацию итеративной регуляризирующей схемы (6) для уравнения (4). Пусть D – двумерная область, в которой заданы неточные значения E_z ( x , y ) , ( x , y ) e D . Тогда операторы в (6) принимают вид:

A * A^z = J jz ( x 5 , У J K ( r , r i; ) dl 5 ; K ( r , r i; ) =    J ^H 01 ) ( kr ) ^H 0 ^{2 )} ( ^kr ) ds ; ( ^x 5 , У ; )^e L';

_L                              16 _D

A * u = i J E z ( x , У ) H 01 ) ( kr ) ds ; ( x ', У ') ^e L ’                                                         (8)

4D r = (x—x')2 +(y—y')2; r = ^(x—x;)2 +(y —y;)2.

В соответствии с выбранным правилом дискретизации D итеративная регуляризирующая схема записывается следующим образом:

j z , n + 1    j z , n

—

ц J j z , n K ( r , r ; ) ^dl ;

_ L

— - J E z H 01 ( kr ) ds

4 _D

; j z ,0 = 0; n = 0,1,2, .

Особую важность при реализации процедуры (9) играют квадратурные формулы повышенной точности для вычисления соответствующих функционалов, обеспечивающие быструю сходимость итеративной процедуры.

Рассмотрим пример, реализующий предложенный подход для решения обратной задачи восстановления. Для контура L в виде окружности радиуса a , ka = 12 исходным для решения обратной задачи рассеяния является поле рассеяния плоской волны на идеально проводящем цилиндре. Область D представляет собой окружность радиуса R = 4 a . Введем следующие параметры аддитивного случайного процесса, интерпретирующие неточно заданные исходные данные: амплитуда amp = 0,1 E_{z max} , фаза phase = 5°. На рис. 1 представлены результаты восстановления АФР тока с помощью итеративной регуляризирующей схемы (6). Число итераций для различных статистических выборок при относительной точности восстановления 10 ^{— 3} не превышает 200, оптимальный параметр ц = 4540. Для сравнения приведены результаты строгого решения задачи определения АФР тока при отсутствии погрешностей исходных данных.

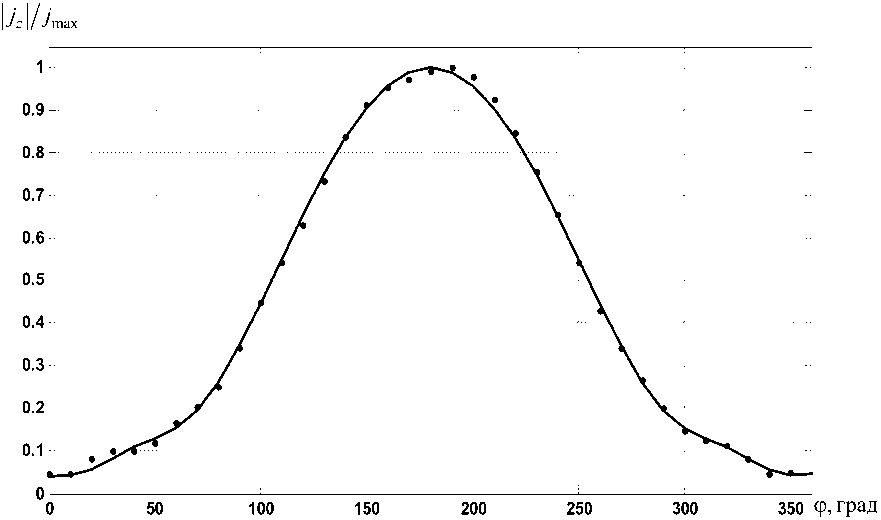
Рис. 1. Амплитудные распределения токов рассеивателя: сплошная линия - строгое решение; • • • - восстановленное АФР

На рис. 2 представлены результаты расчетов поля по восстановленному АФР тока и точное распределение поля плоской волны, соответствующее строгому решению. Для более точных оценок восстановления расчеты поля рассеяния приведены в логарифмическом масштабе.

Большой практический интерес представляет вопрос о границах предложенного метода восстановления, то есть, при каких ошибках в исходных данных можно получить численные результаты, отвечающие достоверным АФР токов и ДН полей рассеяния в рамках выбранных критериев точности. Этот вопрос можно решить с помощью серии вычислительных экспериментов, в частности, для рассмотренного примера срыв достоверного восстановления наступает при amp = 0,34 E_{z ,max} , phase = 25°.

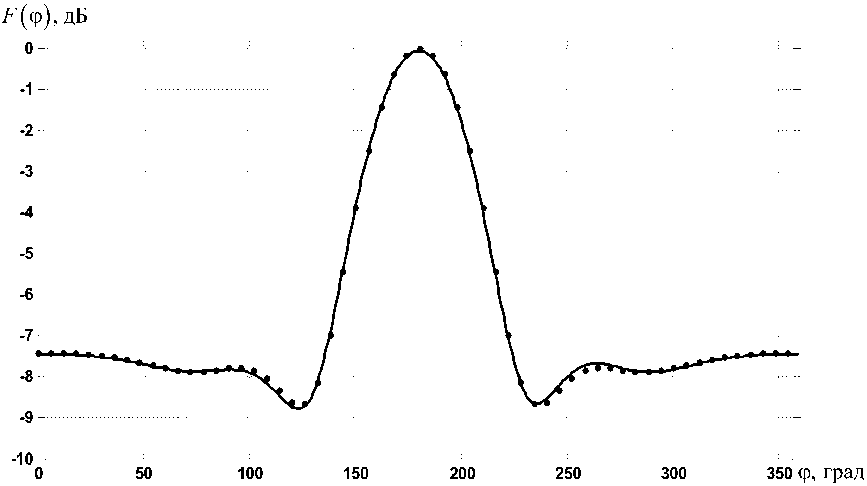
Рис. 2. Амплитудные ДН в дальней зоне: сплошная линия - строгое решение; • • • - восстановленное поле

Сравнение этих результатов иллюстрирует высокую эффективность итеративной регуляри-зирующей процедуры для неточных (зашумленных) исходных данных.

Выводы

• 1.    Для решения обратных задач восстановления АФР токов по неточно заданным исходным данным для напряженности электрического поля принципиально необходимо использование итеративных регуляризирующих схем [6]. Применение прямых методов в этом случае приводит к недопустимо высоким ошибкам восстановления. Переход к 2D задачам особенно эффективен для случая E -поляризации, для этих задач значительно расширяются возможности математического моделирования сложных антенных систем.

• 2.    Сравнение полученных результатов с известными тестовыми решениями показывает высокую эффективность и универсальность предложенных математических моделей некорректных задач.

• 3.    Характерной особенностью итеративных регуляризирующих схем является необходимость тщательного выбора параметра регуляризации µ , зависящего как от свойств исходных данных, так и от свойств дискретной математической модели. При решении практических задач это может приводить к большому объему предварительных вычислительных экспериментов.