Особенности эффекта Доплера в многомодовом волноводе

При отражении волн от движущихся объектов наблюдается изменение частоты отражённых волн (эффект Доплера) [1–9]. Величина этого изменения зависит от соотношения скорости движения объектов и скорости волн в среде [10–14]. Эффект Доплера впервые был обоснован теоретически и подтверждён экспериментально в акустике и оптике. Широкое использование этого физического эффекта в различных областях техники определяет постоянное внимание к нему. В последнее время наблюдается повышенный интерес к эффекту Доплера [3, 14–19] в связи с открытием новых возможностей его использования в различных областях оптики [20–23], микроволновой техники [24, 25], релятивистской техники [26–30], технической акустики различных разновидностей эффекта: аномального, обратного, поперечного, двойного, параметрического [28, 30], сложного, вращательного, релятивистского, сверхсветового [29] и др. Особое внимание уделяется условиям возникновения аномального [10, 11], нелинейного [14, 15], вращательного [14, 17–19] эффектов Доплера, наблюдаемых при взаимодействии излучений с анизотропными, гиротропными и ки-ральными средами и метасредами [20, 21]. Доплеровское смещение спектральных линий было обнаружено в спектрах звёзд и туманностей. В астрофизике эффект Доплера используется для определения скорости движения звёзд, а также скорости вращения небесных тел [2, 4]. Измерения доплеровского красного смещения линий в спектрах излучения галактик привели к выводу о расширении Вселенной. Доплеровское уширение спектральных линий излучения атомов и ионов даёт способ измерения их температуры. В радио- и гидролокации эффект Доплера используется для измерения скорости движущихся объектов. В медицине эффект Доплера используется для диагностики кровеносных сосудов, сердца и т. п. [15, 23].

Эффект Доплера может быть хорошо и наглядно описан геометрическими моделями, что привлекает авторов многих исследований, однако возможности анализа эффекта в этом случае ограничены наиболее простыми конфигурациями [2–5]. Следует отметить, что эффект Доплера рассматривается обычно в пространственно одномерном приближении без учёта поперечного распределения поля [1–5, 8]. Вместе с тем поперечное распределение поля в пространственно ограниченных структурах существенно влияет на особенности волновых процессов [22–25], в том числе на отражение волн от неоднородностей структуры. Влияние различных факторов: движения границ разделов сред, движения самих сред, – сопровождающееся увлечением ими волновых процессов, определяет целесообразность более строгого анализа эффекта отражения от подвижных границ разделов областей на основе теории волновых процессов любой физической природы (электродинамики, акустики и др.) [6, 8]. В настоящей работе рассмотрены особенности отражения волн от подвижного слоя в многомодовой волноводной структуре. Показано, что изменение частоты в эффекте Доплера зависит от скорости движения подвижного слоя и индекса моды распространяющихся волн. В многомодовых волноводных структурах с подвижными неоднородными средами может наблюдаться многочастотный эффект Доплера.

1. Моделирование

Рассмотрим эффект Доплера при отражении основной и высших мод многомодового плоского волновода от слоя магнитодиэлектрика, движущегося вдоль оси волновода. Основные особенности эффекта могут быть рассмотрены на модели плоского волновода (рис. 1). Пусть однородный слой среды 2 толщиной d с показателем преломления n2 = ^£2^2 движется с постоянной скоростью u вдоль оси волновода 0x. Координата левого края слоя описывается во времени зависимостью x = ut, правого: x = ut + d. Слева от границы расположена среда 1, характеризуемая показателем преломления n1 = ^Е1Ц1 . Справа - среда 3 с показателем преломления n3 = ^г3ц3 . Скорость распространения волн в первой среде равна c1 = c/n1, в третьей: c3 = c/n3, с – скорость света в вакууме. Во второй среде с учётом движения среды вдоль оси волновода 0x скорости волн в прямом и обратном направлениях в общем случае различаются c21 ≠ c22 [6]. Для анализа особенностей отражения электромагнитных волн, падающих из области 1 на поверхность подвижного слоя 2, и прохождения волн в область 3 рассмотрим Н (Hx, Ey, Hz) волны.

волновые числа для плоского волновода определяются соотношениями:

^k 11 =

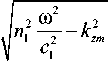
, k ₁₂

k 21

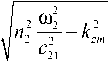
, k ₂₂

^k 31

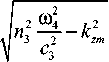
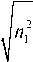
« 2

c ₁ ²

k zm ,

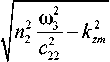
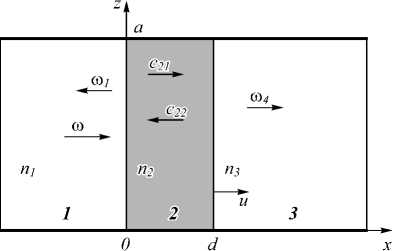
Рис. 1. Отражение и прохождение волн через подвижный слой среды в волноводе

Для кусочно-однородной конфигурации, показанной на рис. 1, преобразования мод на границах раздела сред не происходит. В этом случае распространяющиеся в волноводе моды, характеризуемые индексами m , между собой не взаимодействуют и можно независимо рассматривать распространение и отражение отдельно каждой моды с индексом m .

Подстановка искомых решений в граничные условия для компонент поля E y , H z при x = ut , x = ut + d даёт соотношения между амплитудами A ij и частотами ω i для каждого типа волн с произвольным индексом m , который для простоты записи опускается:

Волновые уравнения в областях 1–3 имеют вид:

д 2 ^д 2      ,2L

ЧТ ⁺ ЧТ ^{+ е} i ^ i k 0 I E y = °. д x д z           J

A 11 e ( «- uk » ) t + a ₁₂ e ( « 1 + u^k 12 ) t = A 21 e ( « 2 - uk 21 >  t + A 2 e

_ ^k 11        i ( ш^{- uk} 11 ) t , ^k 12        i ( «+ uk 12 ) 1_

-A-1 1 e              I         "A"1 2 e

«        ш

,i ( « 3 ^{+ uk} 22 ) t

^^^^^^e

^k 21 A e ( « 2 — uk 21 ) )

« 2    ¹

+ ^k 22 A e ( « 3 ⁺ uk 22 ) t

« 3    ²

Граничные условия на стенках волновода:

E y ( z = °, a ) = 0                                    (2)

и на подвижных границах раздела сред ( x = ut ) имеют вид [6, 24, 25]:

E y ( x ) = E 2 y ( x ), H i z ( x ) = H 2 z ( x ),

E 2 y ( x + d ) = E 3 y ( x + d ),                          (3)

H _{2 z} ( x + d ) = H _{3 z} ( x + d ).

Анализ показывает, что решение существует, когда частоты падающих и отражённых волн в каждом из слоёв в общем случае различны. Решение в каждой из областей ищется в виде:

E 11 _y = A 11 sin k z z • exp [ i ( « ) - k 11 x ) ]

x <  0,

E _{12 y} = A ₁₂ sin k_zz • exp I i ( « 1 t + k ₁₂ x )_ l

E _{21 y} = A 1 sin k z z • exp [ i ( « 2 t — k 21 x ) ]

E _{22 y} = A ₂₂ sin k_zz • exp Г i ( « 3 t + k 22 x ) !

0 <  x <  d , (4)

E31 y = A31 sinkzz • exp[i(«4) - k 31 x)]   x > d, где в общем случае волновые числа прямых и обратных волн могут различаться k11 ≠ k12, k21 ≠ k22.

Проекция волнового числа на ось 0z с учётом граничных условий в плоскостях y =0, y = a равна kzm = mπ/a, m = 1,2,3… – индекс моды. Продольные i «2 d                          i «3 d c21    («2 -uk21 )t             c22   i(«3 + uk22 )t _

^A21 e      e I -A-22 ee

- i«4d(6)

c 31 J ⁽« 4 ^- uk 31 ) t_

-^A31 ee i «2 d                                i «3 d

_ k 21           c 2T j ⁽ « 2 ^- uk 21 ) ⁾,k ₂₂         c 2T 42 ^{i (} « 3 ^{+ u} k 22 ) t _

• -A21 e     e +    -A 22 ee —

«2

• -           - i « 4 d

_    ^k 31            c 31    i ( « 4 ^- uk 31 ) t

• =--A31 ee

« 4

Эти соотношения должны выполняться для любого момента времени t , что приводит к соотношению между частотами волн падающей, отражённой и прошедшей:

«- uk 11 ( « ) = «, + uk₁₂(«_Y) = « 2 - uk ₂₁( « ₂) =

= « 3 + uk ₂₂( « 1 ) ( « 3 ) = « 4 - uk ₃₁( « 1 ) ( « 4 ) ,          ⁽⁷⁾

где частоты: ω 1 – частота волны, отражённой от левой границы подвижного слоя в первой среде, ω 2 – частота волны, прошедшей во вторую среду, ω 3 – частота волны, отражённой от правой границы подвижного слоя 2, ω 4 – частота волны, прошедшей в среду 3. При скорости движения слоя u ≠ 0 все эти частоты отличаются от ω – частоты, падающей на слой волны, и зависят от ряда параметров: от скорости движения границы раздела сред u , от скорости движения каждой из сред υ 1 , υ 2 , υ 3 , от типа волноводной структуры и от индексов распространяющейся моды.

Следует отметить, что соотношения (7) не зависят от типа волноводной структуры и выполняются для различных типов кусочно-однородных вдоль оси 0 z волноводных структур.

2. Основные результаты

Рассмотрим основные особенности, которые вносит вариация поля в поперечном к оси волновода направлении. Из (7) следует, что частота ω 1 отраженной от подвижного слоя волны с индексом m определяется через частоту ω падающей на границу волны с тем же индексом следующим уравнением:

®- u^k 11 m ( ® ) = ® 1 m ⁺ u^k 12m ( « 1 m ) ,                 ⁽⁸⁾

которое для плоской структуры, показанной на рис. 1, может быть представлено в виде:

to-

u n ₁ ²

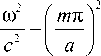
= ® 1 m ⁺ u_A n 1

«L c2

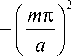
(здесь c 1 = c ). Для волновых чисел падающей и отражённой волн соотношение принимает вид:

k    V n 1 k ^{2 - k} Z2m = ^k 1 m ⁺ “ 4n 1 ^k 1 m — ^k Zm '        ⁽¹⁰⁾

сс

Из (8) – (10) следует, что относительное изменение частоты отражённой волны ω 1 в волноводе, включающем движущуюся границу раздела сред, зависит от относительной скорости движения слоя u / c 1 и номера моды m. Наибольшее изменение частоты наблюдается при скоростях движения неоднородностей структуры и заполняющих её сред, сопоставимых со скоростью распространения волн (акустических или электромагнитных).

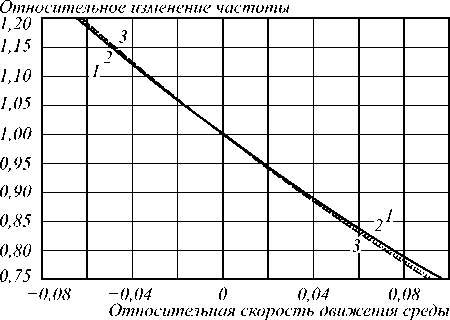
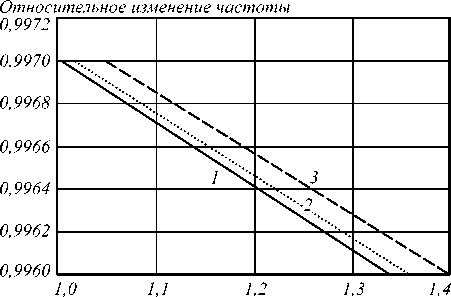
На рис. 2 а , б показана зависимость относительного изменения частоты отражённых волн от относительной скорости движения границы раздела сред u/c для трёх мод. Если слой 2 неподвижен, тогда u/c = 0 и, как и следует ожидать, эффект Доплера не наблюдается (ω 1 /ω = 1). Увеличение частоты (ω 1 /ω > 1) наблюдается при движении слоя навстречу волне ( u/c < 0), уменьшение частоты (ω 1 /ω < 1) наблюдается при «убегании» слоя от волны ( u/c > 0). Увеличение индекса моды приводит к увеличению отклонения относительной частоты m -й моды от относительной частоты эффекта Доплера для модели одномерной структуры. Эта зависимость сохраняется и для прямоугольного волновода, у которого увеличивается число мод с различным поперечным распределением поля.

В третьей области частоты прошедших волн различных мод ω 4 m в общем случае отличаются от частоты волны, падающей на границу раздела подвижного слоя, и определяются уравнением:

to^- uk iim ( to ) = ® 4 m ^- uk 31 m ( « 4 m )■ ⁽¹¹⁾

В частности, для плоской структуры

to-

to 2 2

u      n ₁ ²

c ²

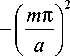
= ^to 4 m

-

u — И2

u 2 n3

a)

б)

Относительная скорость движения среды

Рис. 2. Зависимость изменения частоты ω1m /ω отражённых волн от относительной скорости u/c движения границы раздела сред

(1: m = 1; 2: m = 3; 3: m = 5, πc/ωa = 0,2, n 1 = 1,4)

Если параметры первой и третьей сред одинаковые ( n 1 = n 3 ), тогда в случае прохождения m -й моды без преобразования моды частота прошедшей волны по отношению к частоте падающей волны не меняется ( to 4 m = to ), но, когда прохождение волны сопровождается преобразованием моды, частота меняется. Если параметры 1 и 3 сред разные, то частота прошедшей волны также меняется.

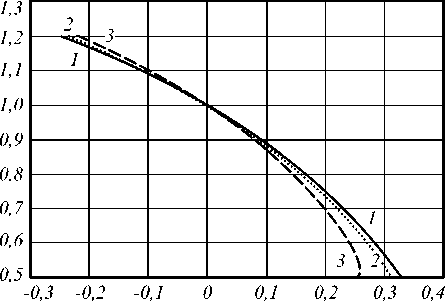
На рис. 3 показана зависимость относительного изменения частоты прошедших волн от относительной скорости движения границы раздела сред u/c для трёх мод. Относительное изменение частоты также зависит от направления движения границы раздела сред и увеличивается с ростом индекса моды. Наиболее значительно эффект проявляется при скоростях движения неоднородностей и сред, сопоставимых со скоростью распространения волн (релятивистский случай [22, 26–28]).

3. Обсуждение

В многомодовой волноводной структуре из-за различия скоростей отдельных мод сдвиг частоты за счёт эффекта Доплера для каждой моды различный. Частоты отражённой волны ω 1 m и прошедшей волны ω 4 m зависят от индекса возбуждаемой моды m . С увеличением индекса моды m скорость изменения частоты отражённой волны в зависимости от скорости

движения границы раздела сред u/c уменьшается, а для прошедшей, наоборот, растёт.

Относительное изменение частоты

Относительная скорость движения среды

Рис. 3. Зависимость изменения частоты ω 4m /ω прошедших волн в зависимости от относительной скорости u/c движения границы раздела сред

(1: m = 1; 2: m = 3; 3: m = 5, πc/ωa = 0,2, n 1 = 1,4, n 3 = 1)

Если граница раздела сред является неоднородной (например, слой переменной толщины), то отражение от границы раздела сред в волноводе сопровождается возбуждением высших мод, и каждой из возбуждённых мод соответствует свой доплеровский сдвиг отражённой и прошедшей волн. Спектры отражённого и прошедшего сигналов обогащаются как увеличением числа мод, так и увеличением числа частот в отражённой и прошедшей волнах (каждой моде соответствует своя частота). Если на границу раздела падает основная волна ( m = 1), частоты отражённых мод ω 1m и частоты прошедших мод ω 4 m определяются уравнениями:

ω

-

u

n

2 ω2

π

-

a

= ω1m

+

u

n 2 ω 1

1 m

-

ω

-

u

ω2

2 n 1

π

-

a

= ω4m

-

u

ω 2 _{4 m} 2 n

-

Движение неоднородного слоя приводит к формированию многомодового режима и соответствующего ему многочастотного эффекта Доплера.

Частоты отражённых и прошедших в третью среду волн всех мод не зависят от параметров второй среды. Отметим, что если параметры первой и третьей сред одинаковые ( n 1 = n 3 ), то прохождение основной моды ( m = 1) не приводит к сдвигу частоты прошедшей волны и ω = ω 41 . Однако частоты прошедших волн более высокого порядка ( m > 1), которые могут возбуждаться неоднородностями структуры, не совпадают с частотой падающей волны (ω ≠ ω 4 m ). В частном случае одномерной структуры ( m =0) для подвижной границы раздела в свободном пространстве ( u/c ≠ 0) имеем известные соотношения для отраженной [1, 2, 4] и прошедшей волн:

с - u с - u

ω1 = 1 ω , ω4 = 1 ω . (15) с1 + u с3 - u

Если граница раздела сред движется в направлении распространения падающей волны (скорости u и c 1 по направлению совпадают), то частота отражённого сигнала меньше частоты падающей волны ω 1 < ω; если граница двигается навстречу падающей волне, то ω 1 > ω. Для прошедшей волны уменьшение или увеличение частоты доплеровского сдвига зависит от соотношения скоростей распространения волн в первой и третьей средах и, если скорости волн в этих средах совпадают, доплеровский сдвиг для прошедших волн не наблюдается.

Изменение частот отражённых и прошедших волн различной физической природы зависит от скорости движения границы раздела сред и скорости самих сред, наблюдается при любых движениях сред. Наиболее сильно этот эффект проявляется при скоростях движения неоднородностей и сред, сопоставимых со скоростью распространения волн. Для электромагнитных волн в этих средах (рис. 2, 3) эти эффекты проявляются при взаимодействии, например, с потоком релятивистских электронов [26] или неоднородностью среды, формируемой волновыми импульсами, в том числе сверхсветовыми, скорость которых в активной среде может превышать скорость света [29]. Рассмотренные эффекты Доплера наблюдаются и для акустических волн в многомодовом волноводе. В этом случае скорость движения неоднородностей, сопоставимая со скоростью распространения волн, встречается достаточно часто.

Заключение

Сдвиг частоты в эффекте Доплера зависит от скорости движения подвижного слоя, от индекса моды волн, скорости распространения которых в волноводе различаются. В многомодовых волноводных структурах с подвижными средами может наблюдаться многочастотный эффект Доплера. Каждой из возбуждённых мод соответствует свой сдвиг частоты отражённого или прошедшего через слой сигнала. Этот сдвиг частоты растёт с увеличением скорости движения подвижного слоя. Доплеровский сдвиг частоты зависит от индекса моды и с ростом индекса степень зависимости уменьшается. Для каждой моды имеется критическое значение скорости движения границы, при превышении которой наблюдается отсечка волнового процесса. Если среды, заполняющие волновод обладают дисперсией частоты, то спектры отражённого и прошедшего через слой сигналов меняются как за счёт эффекта Доплера, так и за счёт дисперсии параметров сред.