Особенности контактных задач для систем струн и балок со слабо закрепленными элементами

PNRPU MECHANICS BULLETIN

Решения ряда контактных задач для струн и балок могут быть получены в явном аналитическом виде [1–10]. В этих задачах контактирующие упругие элементы закреплены так, что каждый из них может оставаться в равновесии при любой приложенной к нему нагрузке, например обе струны и обе балки (рис. 1).

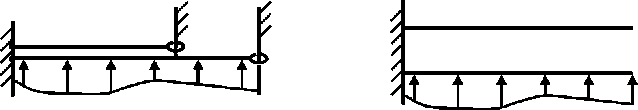
Рис. 1. Системы струн и балок без слабо закрепленных элементов

Возможно, однако, закрепление, при котором для одного из элементов (его можно назвать слабо закрепленным ) это свойство не выполняется, но вся система в целом может находиться в равновесии для достаточно широкого множества внешних (по отношению к системе) нагрузок (рис. 2, 3).

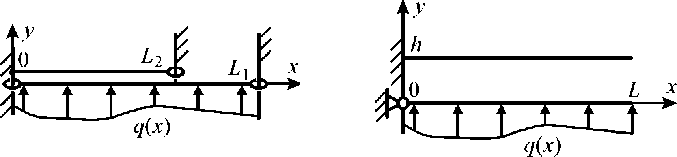
Рис. 2. Система струн со слабо закрепленной нижней струной

Рис. 3. Система балок со слабо закрепленной нижней балкой

Для таких систем постановка контактной задачи, доказательство единственности решения и построение аналитического решения имеют по сравнению с задачами [1-10] некоторые особенности: наличие в постановке задачи условия равновесия слабо закрепленного элемента и наличие дополнительного (подлежащего нахождению наряду с контактными силами) параметра, описывающего неопределенную часть перемещения этого элемента; необходимость доказательства единственности определения не только контактных сил, но и упомянутого параметра; расширение множества допустимых контактных сил; исключение нулевых внешних нагрузок. Эти особенности рассмотрены далее на примере систем, показанных на рис. 2, 3. Заметим, что данные особенности должны проявляться и при численном решении соответствующих контактных задач [11-13], а также в задачах о вдавливании абсолютно твердых свободных тел (штампов) [14-18], что требует отдельного исследования.

1.    Односторонний контакт двух струн

Рассмотрим две струны с различным закреплением концов (см. рис. 2). У первой струны (слабо закрепленный элемент) оба конца свободны; у второй струны левый конец закреплен, правый - свободен; L 1 >  L ₂ - длины струн; T 1 , Т ₂ - натяжения струн; нагрузка с заданной плотностью q ( x ) приложена к нижней струне. Трение между струнами отсутствует. Пусть f ( x ) - плотность сил взаимодействия струн. Из стандартной теории [19] следует, что для первой струны должно выполняться условие равновесия

J f ⁽ x ) dx = J 0 ¹ q ⁽ x ) dx ,                                  ⁽¹⁾

а формы струн при 0 <  x <  L ₂ имеют вид

1 Г x ( г

-^y 1 ^{( x} ) = C ⁺ T J 0 ( J

L ¹ q ( t ) dt - [ L ² f ( t ) dt | ds ,                          (2)

s s )

xL

У 2 ( x ) = J nil f ( t ) dt | ds ,                               (3)

0 s где C - неопределенная постоянная. Контактная задача заключается в отыскании f (x) и C. Будем считать, что функция f (x) имеет вид

p ^{( x} ) ⁺S _г ^{р 5 ( x} - ^x i ),

где p(x) > 0 - кусочно-непрерывна, непрерывна слева при 0 < x < L 2 и непрерывна справа при x = 0 ; Pi > 0 ; xi > 0 (все xi различны); сумма конечна; 5 - дельта-функция Дирака. Заметим, что по сравнению с задачей [7], в которой первая струна также имела закрепленный левый конец, здесь следует расширить множество (4), допустив xi = 0, так как сосредоточенная сила на левом конце теперь влияет на первую струну. Обозначим r(x) = y2(x) - y1(x) (расстояние между струнами). Из (2) и (3) следует, что r (x) = - C + a

Cx(rL ₂              f L 1        A

[ | [ f ( t ) dt - A I    q ( t ) dt | ds

J 0 (J s               J s           )

где a = 1T + V T2, b = VC1 + T /T2).

Будем считать, что q ( x ) >  0 непрерывна при 0 <  x <  L _V, причем q ( x ) ^ 0 (последнее условие необходимо для единственности решения, см. ниже). Условие контакта струн состоит, помимо неотрицательности плотности сил взаимодействия, в том, что расстояние между струнами неотрицательно, а в тех точках, где плотность сил взаимодействия положительна, равно нулю. Окончательно приходим к следующей математической постановке задачи.

Задача 1 . Найти функцию f ( x ) вида (4) и число C такие, что выполнено (1) и при 0 <  x <  L ₂:

/= 0 (f (x) > 0), r (x) 1                                                        (6)

l> 0 (f (x) = 0), где r(x) выражается формулой (5).

Утверждение 1 . Задача 1 может иметь только одно решение.

Доказательство. Пусть f ( x ), C и f * ( x ), C * - два решения задачи 1. По формуле (5) им соответствуют функции r ( x ) и r * ( x ). Обозначим

ф ( x ) = f ( x ) - f * ( x ).                                   (7)

Так как f ( x ) и f * ( x ) имеют вид (4), то ф ( x ) также имеет вид (4), но p ( x ) и P i могут быть неположительными. Обозначим

A = J ² ( r ( x ) — r * ( x ) ) ф ( x ) dx .                                  (8)

Из (6, 7) нетрудно установить, что в (8) подынтегральная функция неположительна, следовательно, A <  0. C другой стороны, подставляя (5) в (8) и учитывая (7), найдем

A =- ( C - C * ) J ² ф ( x ) dx + a J ² J ²( x ) dx ,

где f L 2         ,

J ( x ) =    ф ( s ) ds .

x

Из (1) и (7) следует, что первое слагаемое в (9) равно нулю; тогда из (9) следует, что A >  0. Так как выше было доказано неравенство A <  0, то A = 0. Далее, учитывая (10) и упомянутый выше вид ф ( x ), легко установить, что из (9) и равенства A = 0 следует, что если в ф ( x ) не содержится слагаемое, пропорциональное 5 ( x ), то J ( x ) = 0 при 0 <  x <  L ₂. Тогда можно доказать [7], что ф ( x ) = 0 при 0 <  x <  L ₂. Если же ф ( x ) = P 5 ( x ), то из (1) и (7) следует, что P = 0, то есть ф ( x ) = 0 и в этом случае. Таким образом, f ( x ) = f * ( x ) при 0 <  x <  L ₂. Остается доказать, что C = C * . Из (5) следует, что r ( x ) - r * ( x ) = - ( C - C * ). Если C * C * , то r ( x ) и r * ( x ) не обращаются в нуль одновременно, поэтому при каждом

0 <  x <  L ₂ либо r ( x ) >  0 и тогда f ( x ) = 0 , либо r * ( x ) >  0 и тогда f * ( x ) = f ( x ) = 0, то есть f ( x ) = 0 при 0 <  x <  L ₂. Это противоречит (1) в принятом предположении непрерывной неотрицательной q ( x ) # 0 . Таким образом, C = C * , тем самым утверждение 1 полностью доказано.

Утверждение 2. Решение задачи 1 имеет вид f (x) = F15( x) + F25( x - L 2) + bq (x), C = 0, (11) где

F = (1 - b )f ¹ q ( x ) dx , F ₂ = b l" ¹ q ( x ) dx . (12) J 0 J L ₂

Доказательство. Очевидно, что функция (11) имеет вид (4). Подставляя (11), (12) в (1), нетрудно установить, что (1) выполнено. Подставляя (11) и (12) в (5), найдем, что r ( x ) = 0 при 0 <  x <  L ₂, тем самым (6) выполнено.

Замечание. Функция f ( x ) содержит слагаемое F 1 5 ( x ) ; это означает, что упомянутое выше соответствующее расширение множества допустимых f ( x ) по сравнению с системой [7] (без элементов со слабым закреплением) не является формальным, а определяется существенными свойствами данной задачи.

2.    Односторонний контакт двух балок

Рассмотрим две балки с одинаковыми размерами и физическими свойствами, но с различным закреплением концов (см. рис. 3). У первой балки (слабо закрепленный элемент) левый конец закреплен шарнирно, правый - свободен; у второй балки левый конец защемлен, правый - свободен; E , L , w , H - соответственно модуль Юнга, длина, ширина и толщина каждой балки (сечения балок - прямоугольники); h - расстояние между точками закрепления балок. Трение между балками отсутствует. Пусть f ( x ) - плотность сил взаимодействия балок. Для первой балки должно выполняться условие равновесия

J f(x)xdx = J q(x)xdx.(13)

Из теории Бернулли-Эйлера [20] следует, что упругие линии балок имеют вид xL y1( x) = Cx + al (x - 5) I    (t - 5)(q (t) - f (t)) dt I ds,(14)

• J0         ^Js

xL y 2( x) = h + a (x - s) I    (t - s) f (t) dt I ds ,(15)

• J0         ^J s)

где a = 12/(EwH3); C - неопределенная постоянная. Контактная задача заключается в отыскании f (x) и C. Будем считать, что функция f (x) имеет вид (4), но xt > 0 (не допускается не влияющая на балки сосредоточенная сила на левом конце балок). Обозначим r(x) = y2(x) - y1(x) (расстояние между балками). Из (14) и (15) следует, что xL r (x) = -Cx + h + a (x - s) I    (t - s)(2 f (t) - q(t))dt I ds.                (16)

J ⁰            <  J s                                   )

Будем считать, что q ( x ) >  0 непрерывна при 0 <  x <  L , причем q ( x ) ^ 0. Условие контакта балок аналогично указанному выше условию контакта струн, поэтому приходим к аналогичной математической постановке задачи.

Задача 2 . Найти функцию f ( x ) вида (4) (где x i >  0 ) и число C такие, что выполнено (13) и при 0 <  x <  L выполнено (6), где r ( x ) выражается формулой (16).

Утверждение 3 . Задача 2 может иметь только одно решение.

Доказательство. Пусть f (x), C и f * (x), C* - два решения задачи 2. По формуле (16) им соответствуют функции r(x) и r* (x). Введем ф(x) по формуле (7); эта функция имеет вид, указанный в доказательстве утверждения 1. Введем A по формуле (8) (положив L 2 = L ), тогда аналогично упомянутому доказательству, с одной стороны, A < 0, а с другой стороны, где

A =

- ( C - C * ) J ф ( x ) xdx + 2 a J J ²( x ) dx ,

J ( x ) =f L x

( 5 - x ) ф ( s ) ds .

Из (7) и (13) следует, что первое слагаемое в (17) равно нулю, тогда из (17) следует, что A >  0; так как A <  0, то A = 0 . Далее, учитывая (17) и (18), можно из равенства A = 0 вывести [6], что ф ( x ) = 0, то есть f ( x ) = f * ( x ) при 0 <  x <  L . Остается доказать, что C = C * . Из (16) следует, что r ( x ) - r * ( x ) = - ( C - C * ) x . Если C ^ C * , то r ( x ) и r * ( x ) могут обращаться в нуль одновременно только при x = 0, поэтому при каждом 0 <  x <  L либо r ( x ) >  0 и тогда f ( x ) = 0 , либо r * ( x ) >  0 и тогда f * ( x ) = f ( x ) = 0, то есть f ( x ) = 0 при 0 <  x <  L . Так как кусочно-непрерывная часть f ( x ) непрерывна справа при x = 0 , а 5 ( x ) не может, как предполагалось выше, содержаться в f ( x ), то f ( x ) = 0 при 0 <  x <  L . Это противоречит (13) в принятом предположении непрерывной неотрицательной q ( x ) ^ 0. Таким образом, C = C * , тем самым утверждение 3 полностью доказано.

Утверждение 4. Если Ф(L) > 0, то решение задачи 2 имеет вид f (x) = F 5( x -X) + <

0     (0 <  x < X ),

q ( x )/2   ( X <  x <  L ),

C = a J q (x )(X - x/ 2) xdx +(aX/2)JX q(x)x dx , где

F = ^ (V X ) J 0 q ( x ) xdx + ( 1(2 X ) ) ^ J _x q ( x ) xdx ,

0 < X <  L - корень уравнения Ф ( Л ) = 0,

Ф ( Л ) = [ (2 Л ² - x ²) q ( x ) xdx + Л²[ q ( x ) xdx - 6 h/a .

J 0                                 J л

Доказательство. Существование корня 0 < X < L следует из непрерывности Ф(Л) и значений Ф(0) = - 6h/a < 0, Ф(L) > 0 (единственность корня следует из утверждения 3). Очевидно, что функция (19) имеет вид (4). Подставляя (19) и (21) в (13), нетрудно установить, что (13) выполнено. Подставляя (19)–(23) в (16), можно найти, что r(x) = -Cx + h + a Г (x - 5) | 2(X - 5)F -Г (t - 5)q(t)dt | ds (24) 0 V ss ^

при 0 <  x < X и r ( x ) = 0 при X <  x <  L . Функция f ( x ) может быть положительна только при X <  x <  L , поэтому первое условие (6) выполнено. Остается доказать, что r ( x ) >  0 при 0 <  x < X . Из (24) находим, что r^IV ( x ) <  0 , r ' ( X ) <  0 , r '' ( X ) = 0, тогда либо r " ( x ) >  0 при 0 <  x , либо существует x * такое, что 0 <  x * , r' ' ( x ) <  0 при 0 <  x <  x * и r "( x ) >  0 при x * <  x < X . Из (24) также следует, что r ' (0) <  0 и (с учетом (20)-(23)) r ' ( X ) = 0 . Тогда нетрудно установить, что в обоих упомянутых выше случаях r' ( x ) <  0 при 0 <  x < X . Отсюда с учетом равенства r ( X ) = 0 следует, что r ( x ) >  0 при 0 <  x < X , тем самым второе условие (6) выполнено, и утверждение 4 полностью доказано.

Замечание. Случай Ф ( L ) >  0 возможен: например, при q ( x ) = q ₀ это условие сводится к неравенству q ₀ >  8 h[ ( aL ⁴). Можно показать, что в случае Ф ( L ) <  0 имеется только сосредоточенная контактная сила при x = L .

Выводы

Контактные задачи для систем струн и балок, содержащих слабо закрепленные элементы, имеют особенности, не позволяющие непосредственно применить стандартные схемы постановок и решений, разработанные для систем без таких элементов. Однако можно модифицировать стандартные схемы, сохраняя их основные идеи, и учесть эти особенности; тогда и здесь можно дать строгую постановку контактной задачи и построить в явном виде ее аналитическое решение. Предложенная модификация допускает дальнейшее развитие и распространение на более сложные контактные задачи.