Особенности магнитооптики дихроичных холестерических жидких кристаллов

Получение и исследование новых материалов с управляемыми параметрами остается главной задачей многих исследовательских групп, занимающихся оптикой, фотоникой и материаловедением, поскольку решение проблемы поиска, моделирования, разработки и исследования оптических свойств новых управляемых оптических материалов с заданными характеристиками является важнейшей задачей фотоники и может стимулировать бурное развитие науки и техники. Управление параметрами среды возможно осуществлять внешними (электрическими, магнитными, механическими, акустическими, световыми, тепловыми и т. д.) полями. Интервал возможного изменения соответствующего отклика среды зависит не только от величины соответствующего внешнего поля, но и от параметров самих сред, например от величины магнитооптической активности в случае внешнего магнитного поля и т.д. Эти параметры сред обычно малы, и для изменения отклика среды в значительных интервалах требуются большие поля. Так, например, параметр магнитооптической активности для обычных магнитооптических материалов на оптических частотах порядка 10-3 и меньше [1]. Хорошей управляемостью отличаются жидкие кристаллы (ЖК), их параметрами можно управлять в значительных интервалах относительно слабыми внешними полями. Податливость ЖК к внешним воздействиям привела к возникновению электрооптики и магнитооптики ЖК. Однако существуют критические значения этих полей, при превышении которых происходит разрушение жидкокристаллической структуры [2, 3], например, разрушается спиральная структура у холестерического жидкого кристалла (ХЖК). Кроме того, параметр магнитооптической активности у известных ЖК намного меньше 10 –3. С другой стороны, в последние десятилетия произошли революционные разработки в области материаловедения. Создаются новые материалы с уникальными свойствами (метаматериалы), и в этом аспекте следует отметить следующее: недавно открытые полуметаллы Вейля представляют собой объемные топологические материалы, которые могут проявлять одновременно широкополосный и гигантский магнитооптический эффект даже без внешнего магнитного смещения [4–9]. Так, для полуметаллов Вейля величина Q ~ 1 (Q = g / ε, где g – параметр магнитооптической активности, а ε – диэлектрическая проницаемость среды) [10, 11], т. е. примерно на три порядка больше, чем у обычных магнитоактивных сред. Высокие значения параметра g наблюдались и в других материалах и композитных конструкциях (см., например, [12– 16]). Возникает следующий вопрос: каким образом возможно создать ХЖК-подобные структуры с большим па- раметром g? Суспензии ХЖК различных микро- и наночастиц в последнее время стали предметом возобновленного интереса, поскольку они сочетают в себе текучесть и анизотропию жидких кристаллов с особыми свойствами частиц. Таким образом, растворяя наночастицы с высоким параметром g в ХЖК, мы можем получить структуру типа ХЖК с высоким параметром g. Твердофазные спиральные периодические структуры также могут быть созданы искусственно. Такие среды, но с относительно меньшей анизотропией, были созданы давно [17, 18]. Аналогичным образом могут быть изготовлены тонкие хирально структурированные пленки с высоким параметром g, используя магнитооптический материал с высоким g в качестве источника физического осаждения из паровой фазы. Поэтому в настоящее время является актуальной задачей в фотонике исследование сред типа ХЖК с высокими значениями магнитооптического параметра g, что мы будем делать ниже (см. также [19–23]).

1.    Модели и методология

Рассмотрим отражение и пропускание света через планарный слой ХЖК, находящийся во внешнем магнитном поле, направленном вдоль оси спирали ХЖК. Будем предполагать, что среда обладает спиральной структурой только по отношению к диэлектрическим свойствам, а тензор магнитной проницаемости единичный, т. е. будем предполагать, что тензоры диэлектрической и магнитной проницаемостей имеют вид:

^s ( z ) =

[    1 +8 cos2 az

= s m ±8 sin2 az + ig / s m

V

Ц ( z ) = I ,

±8 sin2 az + ig / s m 1 -8 cos2 az

0 , (1)

0        1 -8)

где s m = ( s i + S 2 )/2, 8 = ( s i - S 2 )/( s i + S 2 ) , £ 1,2 — главные значения локального тензора диэлектрической проницаемости при наличии внешнего магнитного поля, g = g ( H ext )- вектор гирации, a = 2 n / p , p - шаг спирали (пространственный период периодической структуры) при наличии внешнего магнитного поля. Мы рассматриваем случай распространения света вдоль оси спирали.

Известно точное аналитическое решение уравнений Максвелла для ХЖК во внешнем магнитном поле при распространении света вдоль его оси [24]. Согласно [24] дисперсионное уравнение имеет вид:

km + a1 k,2z + a 2 kmz + a 3 = 0,(2)

где

[to2       . , Ito a1 =-21 —- sm + a2 I, a 2 =-4—ag, V c2

a 3 =-2—; a 2s m +—т^гт (1 -82) —- g2 + a4, c2c4

ω – частота и c – скорость света в вакууме.

Используя найденные из (2) собственные значения волновых чисел, решим задачу отражения и пропускания в случае планарного слоя ХЖК. Будем считать, что оптическая ось ХЖК, совпадающая с осью z , перпендикулярна границам слоя. Слой ХЖК с обеих сторон граничит с изотропными полупространствами с одинаковыми показателями преломления, равными n s . Граничные условия, состоящие в непрерывности тангенциальных составляющих электрического и магнитного полей, представляют собой систему из восьми комплексных линейных уравнений с восемью комплексными неизвестными. Решая эту граничную задачу, мы можем определить значения для компонент отраженного E r ( z ) и прошедшего E t ( z ) полей, а также для поля E in ( z ) в самом слое ХЖК и, следовательно, вычислить энергетические коэффициенты отражения R = | E r |² / | E i |², пропускания T = n 2 cos a t | E t |²/ n 1 cos a i | E i |², поглощения A =1 – ( R + T ), и т. д., где n 1 и n 2 – коэффициенты преломления изотропных полупространств соответственно левее и правее слоя ХЖК. При n 1 = n 2 = n s T = | E t |²/ | E i |².

В данной работе мы будем исследовать особенности ХЖК в отсутствие локального двулучепреломления (рис. 1). Задача в этой постановке (рассмотрение предельного случая ReA^ 0, с ImA ^ 0, где A =( s 1 - s ₂)/2) позволяет выявить новые интересные свойства этих сред, что в будущем позволит построить более совершенную магнитооптику спирально сконструированных структур. Современные темпы развития науки и техники позволят также непосредственное создание сред с такими параметрами.

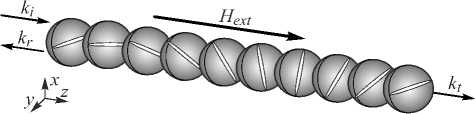
Рис. 1. Геометрия задачи. Серые шарики представляют собой изотропные молекулы ХЖК без двойного лучепреломления, белые линии в этих шариках соответствуют направлениям осцилляторов поглощения, эти направления непрерывно меняются, образуя геликоидальную структуру вдоль оси z

Для численных вычислений мы разработали и использовали алгоритм, который реализован на языке программирования Visual Basic. Ниже все вычисления были сделаны для ХЖК со следующими параметрами: Reɛ 1 = Reɛ 2 = 2,5, шаг спирали ХЖК p =400 нм, толщина слоя d =25 p , спираль ХЖК правая.

2.    Результаты и обсуждение

На рис. 2 представлены спектры пропускания для различных поляризаций падающего света. Длинноволновые пики соответствуют области дифракционного пропускания [20]. Данные среды уникальны тем, что на этой длине волны не только отражение ди- фракционное, но и пропускание здесь также дифракционное (рис. 2б).

Коротковолновые пики (см. рис. 2а) соответствуют области магнитоиндуцированного пропускания (МИП) [21, 22]. Как следует из рис. 2а, МИП является поляризационно-чувствительным эффектом. Этот эффект носит фундаментальный характер и проявляется уже в волновых векторах собственных мод, в чем можно убедиться, исследуя особенности волновых векторов собственных мод.

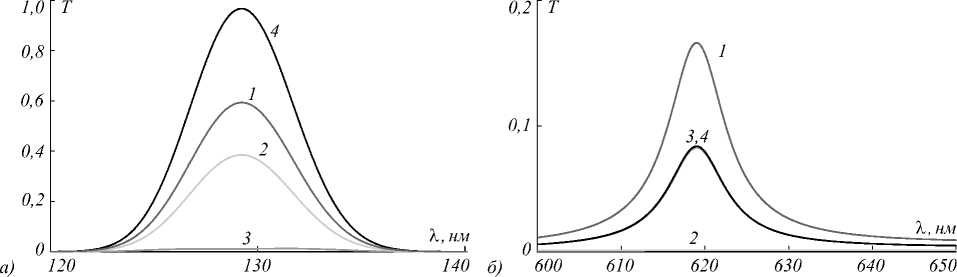
Рис. 2. Спектры пропускания T вблизи области магнитоиндуцированного пропускания (a) и вблизи фотонной запрещенной зоны (б). Падающий на слой свет имеет правую круговую поляризацию (кр.1), левую круговую поляризацию (кр.2), линейную вдоль оси x поляризацию (кр.3) и линейную вдоль оси у поляризацию (кр.4), g = 1,0, Ime i = 0,2, Ime i = 0, n s = elmm

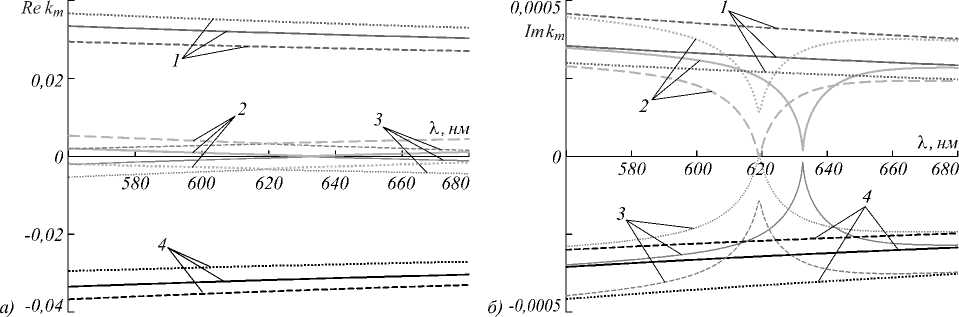
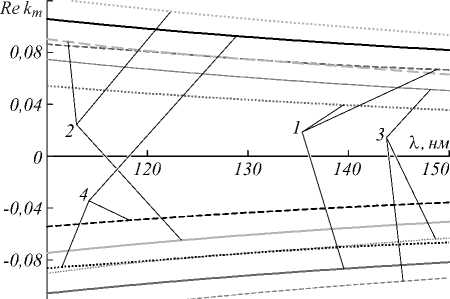
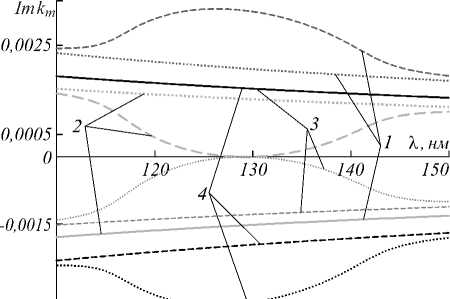
На рис. 3 приведены зависимости реальных и мнимых частей волновых чисел k_mz от длины волны X в следующих трех случаях: 1) g =0 (внешнее магнитное поле отсутствует; сплошные кривые); 2) g =1,0 (внешнее магнитное поле присутствует и параллельно направлению распространения света; штриховые кривые); 3) g = –1,0 (внешнее магнитное поле присутствует и антипараллельно направлению распространения света; пунктирные кривые). Рис. 3 а,б соответствуют области дифракционного отражения, рис. 3 в,г – области МИП.

Как видно из рис. 3, при отсутствии внешнего магнитного поля кривые kmz (λ) симметричны относительно оси kmz =0, что обусловлено взаимностью системы в отсутствие внешнего магнитного поля. Кроме того, существует длина волны X0 = p^Reеm = 632,5нм , где два из четырех Rekm обращаются в нуль. Они являются резонансными волновыми числами [25] при отсутствии локального преломления, и на этой длине волны образуется фотонная запрещенная зона (ФЗЗ). Два других волновых числа соответствуют распространяющимся (в нашем случае поглощающимся) модам, и эти волновые числа мы будем называть нерезонансными. Пронумеруем собственные решения уравнения (2) следующим образом: m = 1 и 4 соответственно для нерезонансных волновых векторов и m =2 и 3 соответственно для резонансных волновых векторов. Внешнее магнитное поле приводит к асимметричному смещению кривых Rekmz (λ) и Imkmz (λ) относительно оси kmz =0, возникает невзаимность. При g > 0 реальные части кривых k1,4z (λ) смещены вниз, а кривых k2,3z (λ) смещены вверх, для мнимых частей имеем обратную картину. При g < 0 мы имеем противоположную картину. Заметим также, что длина волны λr, на которой кривые реальных частей резонансных волновых чисел k2z (λ) и k3z (λ) пересекаются и при g > 0, и при g < 0, смещаются в сторону ко- ротких волн по отношению к λ0. Отметим еще одну особенность. Как видно из рис. 3в, на определенной длине волны (при λt = 128,9 нм для данных параметров задачи) значение Imk2z равно нулю, то есть на этой длине волны среда прозрачна для этой моды, хотя Imɛ1 ≠ 0. Далее сравнение этих кривых с аналогичными в случае ReΔ ≠ 0 в [21] показывает существование определенной симметрии относительно оси kmz = 0 в области МИП, которая отсутствует в случае ReΔ ≠ 0 [21].

Переходим к исследованию особенностей локализации света. Особенности локализации света в фотонных структурах – сравнительно новая и важная задача оптики и фотоники, а также биофотоники и имеет как фундаментальное теоретическое значение, так и важное практическое применение в самых различных областях науки и техники. Особенности локализации света, фотонной плотности состояния и люминесценции в ХЖК исследованы в работах [26– 39]. Ниже мы продолжаем исследовать особенности локализации света в слое ХЖК при наличии внешнего магнитного поля, что является важным для создания управляемых магнитооптических устройств, лазеров и др. Суммарное электрическое поле, соответствующее среде на левой стороне дихроичного слоя ХЖК, в самом слое ХЖК и среде на правой стороне слоя ХЖК (мы предполагаем, что слой ХЖК расположен между двумя изотропными полупространствами z = 0 и z = d ) можно представить следующим образом:

f E , ( z ) + E r ( z ), z <  0,

E ( z ) =1 e ,„ ( z ), 0 <  z <  d ,                          (3)

^Et (z), z > d, где Ein(z) – полное электрическое поле в слое ХЖК.

в) -0,12

Рис. 3. Зависимости реальных и мнимых частей волновых чисел k mz от длины волны λ при различных значениях параметра магнитооптической активности g. Параметры те же, что и на рис. 2

г) -0,0035

На рис. 4 представлены зависимости I ( z )=| E ( z )|² на длине волны λ 0 и λ r при различных значениях параметра g (рис. 4 а,б ), на различных длинах волн при g =0,5 (рис. 4 в ) и на длине волны λ t при g = 1,0 (рис. 4 г ). Падающий на слой свет имеет правую (рис. 4 а,в,г ) и левую (рис. 4 б ) круговые поляризации.

Известно, что при взаимодействии электромагнитной волны со слоем фотонного кристалла периодические неоднородности последнего приводят к модуляции суммарной волны, возникающей в среде. У обычных ХЖК с локальным двулучепреломлением существует ФЗЗ конечной частотной ширины. Одна из круговых поляризаций падающей волны, знак которой противоположен знаку хиральности ХЖК, не испытывает дифракции, причем амплитуда суммарной волны, возникающей в среде, практически постоянная и практически точно совпадает с амплитудой падающей волны (при минимальном влиянии диэлектрических границ, т. е. при n s =ε m ) [38].

Суммарная стоячая волна, возбуждаемая в среде, модулирована и имеет особенности модуляции для падающего света с дифрагирующей круговой поляризацией. Причем характер изменения амплитуды этой волны в зависимости от z внутри ФЗЗ и вне ФЗЗ существенно отличаются друг от друга. Внутри ФЗЗ амплитуда стоящей волны экспоненциально уменьшается с увеличением z, волна эванесцентная и уже при z порядка 20 ÷ 30p она практически равна нулю – происходит дифракционное отражение [38]. Вне ФЗЗ амплитуда суммарной волны совершает различным образом модулированные (для различных длин волн) осцилляции [38].

В отсутствие локального двулучепреломления, т.е. при ReΔ =0, ImΔ ≠ 0, при падении на слой света с дифрагирующей круговой поляризацией амплитуда суммарной волны, возбуждаемой в слое ХЖК, уменьшается с увеличением z . Однако из-за дифракции на такой структуре данное уменьшение амплитуды происходит не по экспоненциальному закону (рис. 4 a ), как это имеет место при наличии локального двулучепреломления для волн внутри ФЗЗ. Наличие внешнего магнитного поля приводит к появлению осцилляции в зависимости | E ( z )|² и к увеличению накопленной в слое световой энергии (рис. 4 а ).

С увеличением параметра g амплитуда этих осцилляций увеличивается. И наоборот, при падении света с левой (недифрагирующей) круговой поляризацией, амплитуда суммарной волны, возбуждаемой в слое ХЖК, уменьшается с увеличением z именно по экспоненциальному закону (рис. 4б), и это естественно, так как для недифрагирующей круговой поляризации данная среда представляет собой практически изотропную поглощающую среду. Для этой поляризации падающего света характер зависимости |E(z)|2 практически не меняется с изменением длины волны и претерпевает незначительные изменения по вели- чине. Заметим, что при наличии локального двулучепреломления и при отсутствии поглощения, для падающей волны с недифрагирующей круговой поляризацией, как было отмечено выше, суммарное поле практически не меняется с изменением z. На рис. 4в показаны зависимости I (z) = |E(z)|2 для других (находящихся в непосредственной близости от ФЗЗ) длин волн падающего света с дифрагирующей круговой поляризацией. Из этих рисунков следует, что характер зависимостей мало меняется, они отличаются по величине и мере удаления от резонансной частоты, при этом по мере удаления от резонансной частоты характер зависимости приближается к эванесцентно-му, поскольку уменьшается роль дифракции и начинает основную роль играть поглощение. Для света с недифрагирующей круговой поляризацией характер зависимости |E(z)|2 не меняется с изменением длины волны и меняется незначительно также по величине. И, наконец, на длине волны МИП λt величина |E(z)|2 постоянная (величина которой меняется с ns) в среде и имеет осцилляции (амплитуда которых зависит от ns) вблизи правой границы слоя ХЖК.

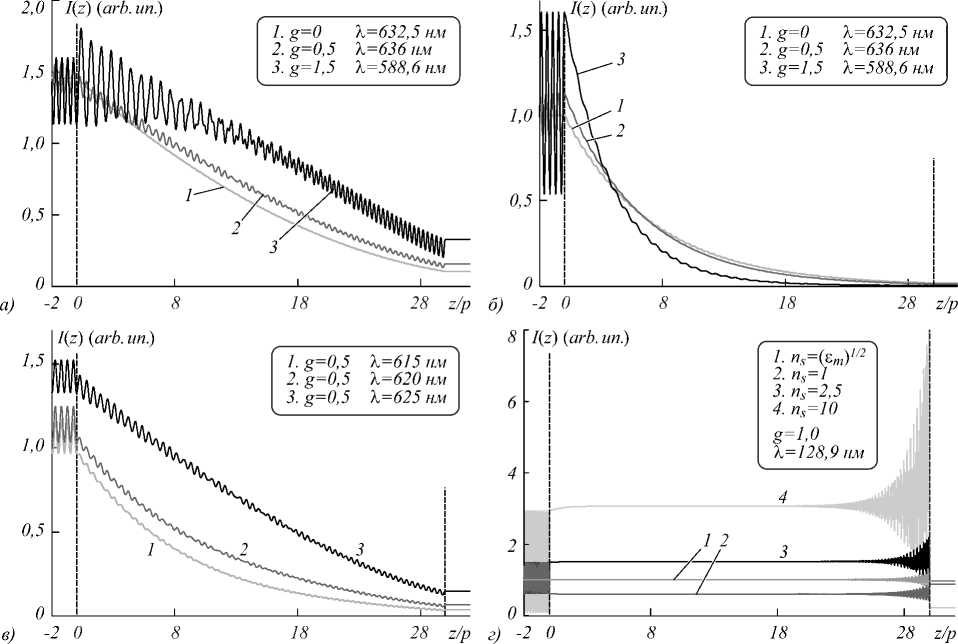
Рис. 4. Зависимости I(z)=| E (z)|², параметры те же, что и на рис. 2

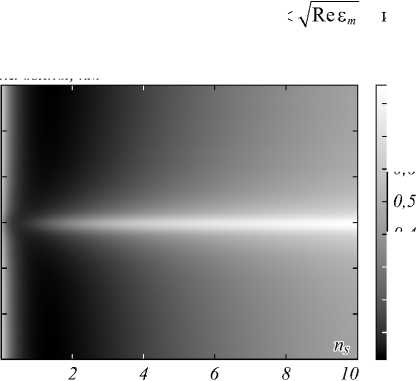
Переходим к исследованию влияния диэлектрических границ на отражение и пропускание света через слой ХЖК. На рис. 5 представлены эволюции спектров отражения при изменении n s вблизи длины волны резонанса λ r . Падающий на слой ХЖК свет имеет линейную вдоль оси x поляризацию (рис. 5 а ) и линейную вдоль оси y поляризацию (рис. 5 б ), а также левую круговую поляризацию (рис. 5 в ) и правую круговую поляризацию (рис. 5 г ). Качественно такие же зависимости наблюдаются и при g =0, отличие только в том, что длина волны резонанса в этом случае испытывает красный сдвиг, а именно λ 0 = 632,5 нм (при g = 1,0 имеем λ r =618 нм). Рис. 5 а – г демонстрируют сильное влияние n s на отражение.

На рис. 6 представлены эволюции спектров пропускания при изменении n s вблизи длины волны резонанса λ r .

Падающий на слой ХЖК свет имеет правую круговую поляризацию (рис. 6 а ) и линейную вдоль оси x поляризацию (рис. 6 б ). Пропускание при падении света с левой круговой поляризацией отсутствует, а эволюция спектров пропускания при падении на слой света с линейной вдоль оси y поляризации практически такая же, как на рис. 6 б . Опять, как и выше, рис. 6 демонстрирует существенное влияние на пропускание параметра n s , от значительного пропускания на длине волны резонанса при ns ~ у] Re е m до его полного исчезновения при ns <<  у/ Re е m и при ns >>  у/ Re е m .

На рис. 7 представлены эволюции спектров пропускания при изменении n s вблизи длины волны МИП λ t .

Падающий на слой ХЖК свет имеет линейную вдоль оси x поляризацию (рис. 7 а ) и линейную вдоль оси y поляризацию (рис. 7 б ), а также правую круговую поляризацию (рис. 7 в ) и левую круговую поляризацию (рис. 7 г ). Как видно из рис. 7, эффект МИП

Длина волны, нм 680

а)

Длина волны, нм 680

в)

0,9 0,8 0,7 0,6 0,5 0,4 0,3

0,2 0,1

0,7

0,6

0,5

0,4

0,3

0,2

0,1

имеет место только при опред еленн ом интервале из-

менения n s вблизи

б)

.

- 0,8

- 0,7

АО,6

значения J Re sm . При определён-пропускание вообще может исче- это имеет ных значениях ns место при ns <<

Re s m

Длина волны, нм 680

зать, ns >>

и при

0,4

0,3

0,2

0,1

- 0.8

Дли на волны, нм б^ог^™™

620 -

" 0,7

0,6

0,5

0,4

0,3

0,2

0,1

г)

Рис. 5. Эволюция спектров отражения при изменении n s в области формирования ФЗЗ.

Параметры те же, что и на рис. 2

а)

Длина волны, нм

Рис. 6. Эволюция спектров пропускания при изменении ns в области формирования ФЗЗ, параметры те же, что и на рис. 2

Длина волны, нм 680

0,08 0,07 0,06

0,05 0,04 0,03

0,02 0,01 О

• б)

Заключение

В работе исследованы магнитооптические свойства слоя дихроичного ХЖК при больших значениях магнитооптического параметра g. Получены особенности всех решений дисперсионного уравнения в деталях как вблизи длины волны резонанса, так и вблизи длины волны МИП. Сравнение результатов для локально дихроичных ХЖК вблизи длины волны МИП с аналогичными результатами в случае ХЖК с локальным двулучепреломлением (см. [21]) показывает существование определенной симметрии относительно оси kmz =0, которая отсутствует в случае ReΔ ≠ 0, т. е. в случае ХЖК с локальным двулучепреломлением. Исследование особенностей локализации света показало, что наличие внешнего магнитного поля, как и отличие ns от д/Re sm , т. е. наличие диэлектрических границ, приводит к появлению осцилляций в зависимостях |E(z)|2.

В областях образования ФЗЗ и МИП исследованы особенности отражения и пропускания света и влияния на них диэлектрических границ. Показано сильное влияние параметра ns на оптику рассматриваемого слоя. В частности, показано, что МИП и дифракционное пропускание возникают только при определенных интервалах изменения параметра ns вокруг значения

Re s m . МИП и диф ракци онное про пускан ие исчезают в пределах n s <<  Re s m и n s >> ^ Re s m .

а)

б)

0,9 0,8 0,7

0,6 0,5 0.4

0,3 0.2 0.1

О

Длина волны, нм 150

ВО

в)

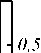
Длина волны, нм 150

ВО

г)

0.35

0,30

0,25

0,20

0,15

0,10

0,05 О

Рис. 7. Эволюция спектров пропускания при изменении n s в области формирования МИП,

параметры те же, что и на рис. 6

Работа выполнена при поддержке Министерства науки и высшего образования в рамках выполнения работ по Государственному заданию РФ, проект FZNS-2020-003 №0657-2020-0003.