Особенности математического моделирования доплеровского преобразователя для определения параметров перемещений лопаток энергоагрегатов

Наиболее простую конструкцию имеют ав-тодинные преобразователи, регистрирующие сигнал в цепи питания генератора [3]. СВЧ излучение, отраженное от поверхности жестко закрепленной в колесе лопатки, воздействует на диод Ганна и изменяет его энергетические параметры, тем самым вызывая колебания тока в цепи его питания. Информационный сигнал в данном случае будет описываться уравнением:

5 ( t ) = A ( t )sin( ® D • t + Ф о ) , где A ( t ) , ^ D , Ф о — амплитуда, частота и начальная фаза информационного сигнала на выходе доплеровского преобразователя соответственно;

Рассмотрим особенности математического моделирования информационных изменений амплитуды, частоты и фазы выходного сигнала доплеровского преобразователя.

На рис. 1 представлена графическая модель системы для определения мощности информационного потока P_прм , попадающего в приемник после отражения от поверхности лопатки, пересекающей при своем движении поток излучения доплеровского преобразователя [2].

Мощность информационного потока принятого приемником может быть определена по формуле:

ji

Р = Р ZIP • D прм изл pизлij p прмij , n=1k=1

где P_изл – мощность зондирующего излучения первичного преобразователя;

p_излi j – весовой коэффициент мощности излучения i -го луча j -го точечного излучателя;

p_прмi j – весовой коэффициент мощности принятого i -го луча j -го точечного излучателя;

В прямоугольной системе координат XYZ расположен приемно-передающий элемент доплеровского преобразователя, излучающая поверхность которого совпадает с плоскостью ХOZ , а центр этой плоскости совпадает с началом отсче-

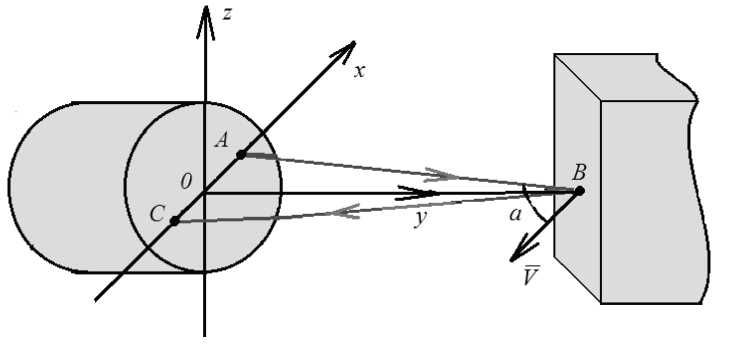
Рис. 1. Схема взаимодействия автодинного преобразователя с поверхностью лопатки

та. Излучаемый автодином поток представляется пучком лучей, который формируется совокупностью точечных излучателей, равномерно распределенных внутри круга радиуса r . Круг разбивается на кольца шириной Δ , каждому кольцу соответствует весовой коэффициент интенсивности излучения, которое имеет нормальное распределение в плоскости доплеровского преобразователя. Таким образом формируется зондирующее излучение в направлении поверхности контролируемой лопатки. Поскольку геометрические размеры лопатки во много раз превышают размеры сформированного точечного излучателя, то можно воспользоваться аппаратом геометрической оптики для определения потока, отраженного от поверхности наблюдаемого объекта и попадающего на приемник [4].

Разбиение излучающей поверхности преобразователя на точечные источники представлено на рис. 2.

Луч, отраженный от поверхности наблюдаемого объекта, падает на активную зону приемника, которая также разбита на кольцевые участки с весовыми коэффициентами соответствующими распределению интенсивности принятого излучения в плоскости преобразователя.

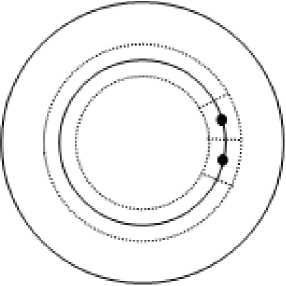
Рис. 2. Разбиение излучающей поверхности преобразователя на точечные источники

В качестве объекта наблюдения выбрана лопатка идеальной прямоугольной формы установленная в лопаточном колесе под углом 45 градусов к оси излучателя.

На рис. 3 представлено сечение рассматриваемой системы плоскостью ХОY , и отмечены характерные положения лопатки в активной зоне датчика. Точечные излучатели на границах приемно-передающего элемента автодинного преобразователя обозначены i ₁ и i ₂ . На рис. 4 приведена зависимость амплитуды выходного сигна-

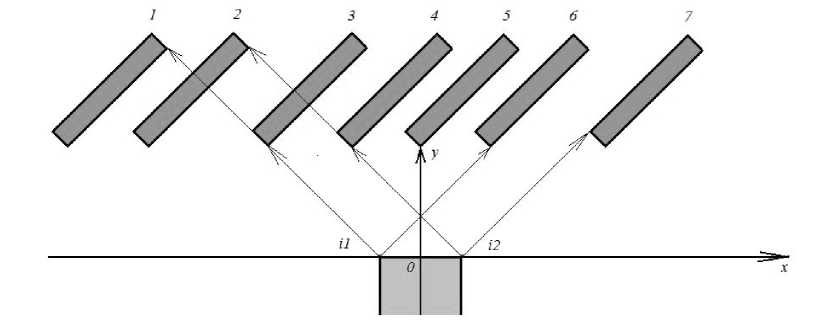
Рис. 3. Сечение моделируемой системы плоскостью ХОY

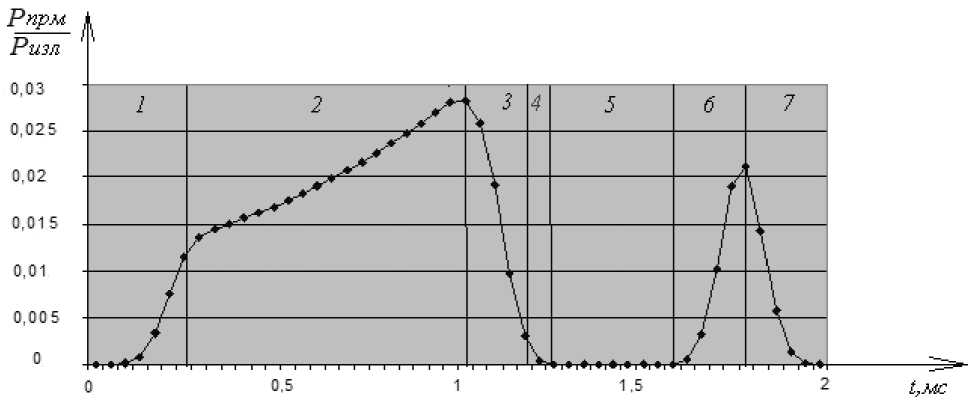
Рис. 4. Изменение амплитудной компоненты выходного сигнала автодинного преобразователя для исследуемой прямоугольной лопатки

ла автодинного преобразователя от координат расположения лопатки в активной зоне датчика.

В момент времени, когда лопатка находится в зоне 1, на автодин попадают первые лучи излучателя i _x , отразившиеся от поверхности лопатки и на выходе преобразователя начинает формироваться передний фронт сигнала. До этого момента сигнал на выходе автодинного преобразователя равен нулю. В процессе вращения диска, лопатка переходит в зону 2, которая характеризуется тем, что на лопатку начинают попадать лучи от всех точечных источников излучения ( / 1 и i 2 ), при этом амплитуда сигнала на выходе преобразователя продолжает нарастать, но фронт имеет меньшую крутизну. В зоне 3 поверхность лопатки становится недоступна для части лучей точечного излучателя / 1 и амплитуда сигнала начинает падать, до момента пока лопатка не выйдет из зоны 4 и автодин не перестанет принимать отраженный сигнал. В зоне 5 сигнал, отраженный от лопатки не попадает на приемник и на выходе доплеровского преобразователя амплитуда сигнала равна нулю. Когда лопатка переходит в зону 6, на выходе автодинного преобразователя вновь появляется нарастающий фронт сигнала, что обусловлено отражением лучей точечного излучателя / 1 от поверхности лопатки. Затем на выходе доплеровского преобразователя появляется спадающий фронт сигнала, до тех пор, пока лопатка не окажется в зоне 7 и не выйдет из активной зоны датчика.

Частота доплеровского сигнала на выходе автодинного преобразователя определяется известным выражением:

fD(t) = —V cos(a) ,       (1)

с где fo – рабочая частота генерации автодин-ного преобразователя, c – скорость света; V – проекция мгновенной линейной скорости лопатки на ось x в точке падения зондирующего луча на ее поверхность; а — угол между осью диаграммы направленности датчика и направлением движения объекта.

Скорость движения лопатки в точке падения зондирующего луча определяется выражением:

V = to R [ R + A z ( t )] , (2) где A z — проекция зондирующего луча на ось z системы координат изображенной на рис. 1.

Угол между зондирующем лучом датчика и направлением движения объекта, определяется по формуле:

а = arctg (

A yt )) A x ( t )

где A x = OA , A y = OB - проекции зондирующего луча, попавшего на поверхность лопатки, на соответствующие оси системы координат изображенной на рис. 1;

Подставив выражения (2) и (3) в формулу (1), получим зависимость доплеровской частоты от времени:

^fD ⁽ t ) =    ° ^to R

с

[R + Az(t)]cos arctg(-^y^) ._       Ax (t) _

На рис. 5 представлена зависимость частоты доплеровского сигнала от времени.

Форма сигнала на выходе автодинного преобразователя также зависит от его начальной фазы. На рис. 6 представлена зависимость часто-

„  3n

ты доплеровского сигнала от времени с фазой    .

При фазовом сдвиге отличном от нуля на центральном пике выходного сигнала начинает формироваться характерный провал.

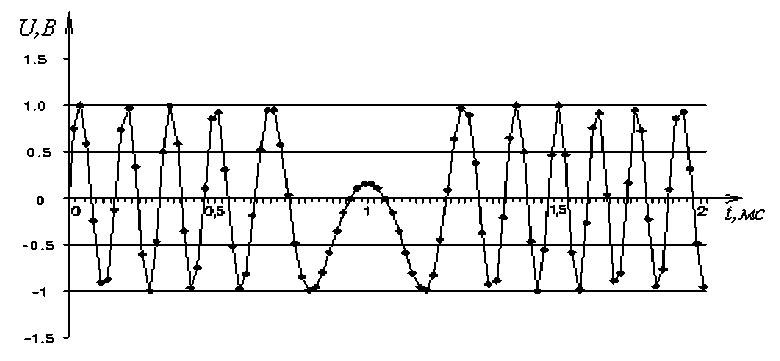
Рис. 5. Зависимость частоты доплеровского сигнала от времени

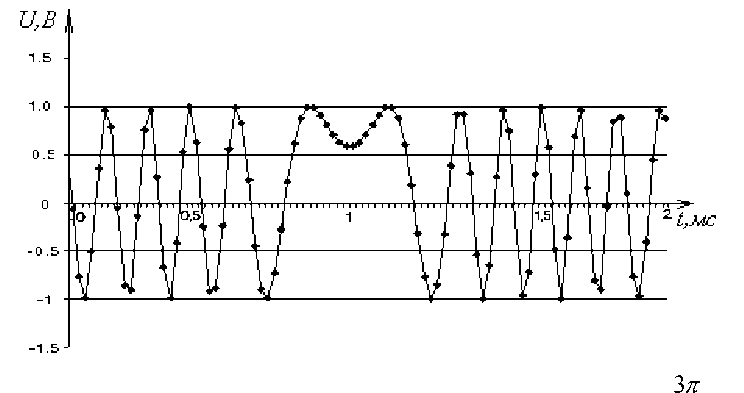
Рис. 6. Зависимость частоты доплеровского сигнала сдвинутого по фазе на    от времени

Учитывая приведенные особенности моделирования выходного сигнала доплеровского преобразователя, составлен алгоритм вычислений потока, попадающего на фотоприемник. На основании этого алгоритма разработана компьютерная программа, реализующая на языке Pascal, метод численного интегрирования. В программе были учтены граничные условия и исходные данные, принятые в рассматриваемой системе.

Для проверки полученных теоретических положений был проведен эксперимент, который был реализован на установке, имитирующей лопаточное колесо, со следующими параметрами:

Диаметр лопаточного колеса, R : 123мм;

Длина лопатки, l :                20 мм;

Ширина лопатки, b :            14мм;

Толщина лопатки, h :             2 мм;

Минимальное расстояние от кромки лопатки до доплеровского преобразователя: 7,5мм;

Ширина диаграммы направленности доплеровского преобразователя, Θ : 120 градусов;

Количество лопаток в колесе: 7;

Частота вращения лопаточного колеса, ω _R : 2 π 50 рад ;

с

На рис. 7 изображена амплитуда выходного сигнала доплеровского преобразователя полученная в результате эксперимента.

Можно заметить, что амплитуда доплеровского сигнала, полученного в результате моделирования перемещения прямоугольной лопатки, отражающие плоскости которой представлены аналитическими выражениями, и лопатки, используемой в эксперименте, заметно отличаются. Это обусловлено тем что, у лопаток экспериментального стенда при механической обработке скруглены кромки. В результате данного скругления была сформирована отражающая поверхность, формирующая пик на амплитудной характеристике.

На рис. 8 и 9 представлены сигналы на выходе автодинного преобразователя полученные в результате математического моделирования и в результате эксперимента соответственно.

Таким образом, можно констатировать, что сигнал, полученный в результате математического моделирования взаимодействия зондирующего потока с контролируемой поверхностью совпадает по форме с данными полученными во время эксперимента. Следовательно, в доплеров-

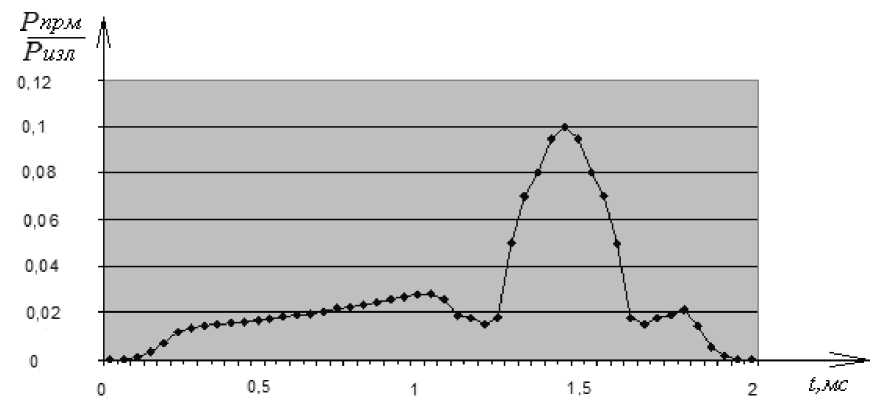
Рис. 7. Амплитуда сигнала на выходе автодинного преобразователя

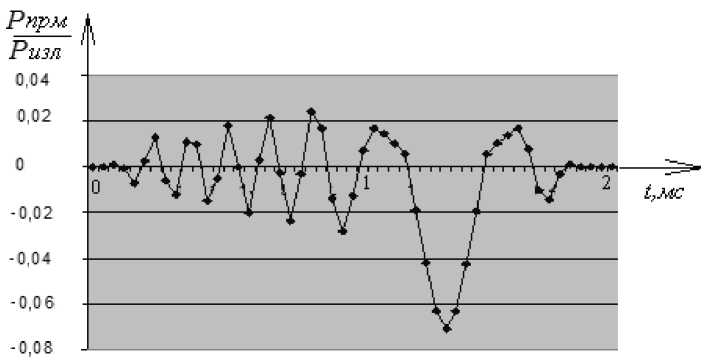
Рис. 8. Сигнал, полученный на выходе автодинного преобразователя

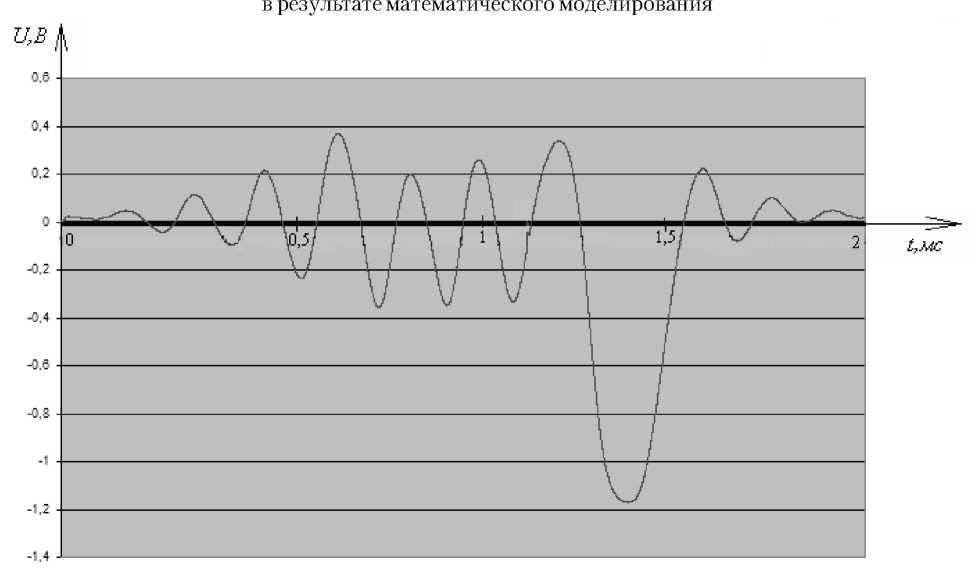
Рис. 9. Сигнал, полученный на выходе автодинного преобразователя в результате эксперимента ском сигнале содержится информация о частоте вращения лопаточного колеса и форме поверхности лопатки. В дальнейшем данная математическая модель может быть уточнена и дополнена компонентами, учитывающими колебательные перемещения лопатки, что позволит определять параметры этих колебаний по экспериментальным данным.